Difference between revisions of "Diagy Alwan Irsyad"
| Line 45: | Line 45: | ||
=== Pertemuan III (25 November 2020) === | === Pertemuan III (25 November 2020) === | ||
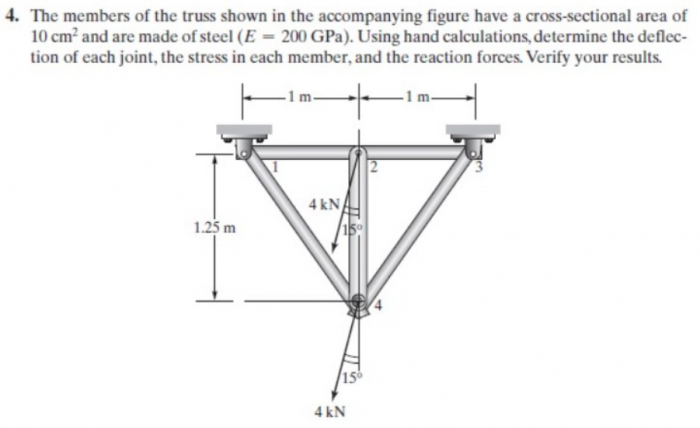
==== Finite Element Method for Trusses ==== | ==== Finite Element Method for Trusses ==== | ||
| − | |||
| + | [[File:SoalTrusses4 d29.png|700px|thumb|left]] | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 52: | Line 52: | ||
''Persamaan'' | ''Persamaan'' | ||
| − | + | class Trusses_Tugas3_d29 | |
| − | parameter Integer N= | + | parameter Integer N=8; //Global matrice = 2*points connected |
| − | parameter Real A= | + | parameter Real A=0.001; //m^2 |
| − | parameter Real E= | + | parameter Real E=200e9; //Pa |
Real G[N,N]; //global | Real G[N,N]; //global | ||
Real Ginitial[N,N]; //global | Real Ginitial[N,N]; //global | ||
| − | Real Sol[N]; //global | + | Real Sol[N]; //global displacement |
| − | Real X[N]={0,0, | + | Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033}; |
Real R[N]; //global reaction force | Real R[N]; //global reaction force | ||
Real SolMat[N,1]; | Real SolMat[N,1]; | ||
Real XMat[N,1]; | Real XMat[N,1]; | ||
| − | //boundary | + | //boundary condition |
Integer b1=1; | Integer b1=1; | ||
Integer b2=3; | Integer b2=3; | ||
//truss 1 | //truss 1 | ||
| − | parameter Real X1=0; //degree between | + | parameter Real X1=0; //degree between trusses |
| − | Real k1=A*E/ | + | Real k1=A*E/1; |
| − | Real K1[4,4]; //stiffness | + | Real K1[4,4]; //stiffness matrices |
Integer p1a=1; | Integer p1a=1; | ||
Integer p1b=2; | Integer p1b=2; | ||
| Line 78: | Line 78: | ||
//truss 2 | //truss 2 | ||
| − | parameter Real X2= | + | parameter Real X2=0; //degree between trusses |
| − | Real k2=A*E/ | + | Real k2=A*E/1; |
| − | Real K2[4,4]; //stiffness | + | Real K2[4,4]; //stiffness matrices |
Integer p2a=2; | Integer p2a=2; | ||
Integer p2b=3; | Integer p2b=3; | ||
| Line 86: | Line 86: | ||
//truss 3 | //truss 3 | ||
| − | parameter Real X3= | + | parameter Real X3=90; //degree between trusses |
| − | Real k3=A*E/ | + | Real k3=A*E/1.25; |
| − | Real K3[4,4]; //stiffness | + | Real K3[4,4]; //stiffness matrices |
| − | Integer p3a= | + | Integer p3a=2; |
Integer p3b=4; | Integer p3b=4; | ||
Real G3[N,N]; | Real G3[N,N]; | ||
| − | + | ||
//truss 4 | //truss 4 | ||
| − | parameter Real X4=90; //degree between | + | parameter Real X4=90+38.6598; //degree between trusses |
| − | Real k4=A*E/ | + | Real k4=A*E/1.6; |
| − | Real K4[4,4]; //stiffness | + | Real K4[4,4]; //stiffness matrices |
| − | Integer p4a= | + | Integer p4a=1; |
Integer p4b=4; | Integer p4b=4; | ||
Real G4[N,N]; | Real G4[N,N]; | ||
//truss 5 | //truss 5 | ||
| − | parameter Real X5= | + | parameter Real X5=90-38.6598; //degree between trusses |
| − | Real k5=A*E/ | + | Real k5=A*E/1.6; |
| − | Real K5[4,4]; //stiffness | + | Real K5[4,4]; //stiffness matrices |
| − | Integer p5a= | + | Integer p5a=3; |
| − | Integer p5b= | + | Integer p5b=4; |
Real G5[N,N]; | Real G5[N,N]; | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
/* | /* | ||
| − | for each truss, | + | for each truss, ensure pXa is lower then pXb (X represents truss element number) |
*/ | */ | ||
| Line 139: | Line 131: | ||
G5:=k5*Local_Global(K5,N,p5a,p5b); | G5:=k5*Local_Global(K5,N,p5a,p5b); | ||
| − | + | G:=G1+G2+G3+G4+G5; | |
| − | |||
| − | |||
| − | G:=G1+G2+G3+G4+G5 | ||
Ginitial:=G; | Ginitial:=G; | ||
| Line 166: | Line 155: | ||
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat); | R:=Reaction_Trusses(N,Ginitial,SolMat,XMat); | ||
| − | end | + | end Trusses_Tugas3_d29; |
|} | |} | ||
Revision as of 14:55, 2 December 2020
Biodata
Nama : Diagy Alwan Irsyad
NPM : 1906301154
Angkatan : 2019
Program Studi : Teknik Mesin, S1 Reguler
Tempat, tanggal lahir : Cepu, 29 April 2001
Jenis kelamin : Laki-laki
Alamat surel : diagya.irsyad29@gmail.com / diagy.alwan@ui.ac.id
Metode Numerik-02
Pada semester gasal 2020/2021, saya mengambil mata kuliah Metode Numerik, tepatnya di kelas Metode Numerik-02.
Contents
[hide]Pertemuan I (11 November 2020)
Pertemuan pertama bersama Pak Dai, saya dan mahasiswa lain diajak berpikir untuk bisa mengetahui hal-hal yang sudah kami ketahui dan yang belum. Dengan mengetahui hal yang belum diketahui, kami bisa mempelajari hal-hal tersebut.
Selain itu, kami juga membahas tentang pengenalan aplikasi OpenModelica. Di akhir kelas, kami diberi tugas untuk membuat video mengenai cara penggunaan OpenModelica.
Berikut adalah video yang saya buat:
Pertemuan II (18 November 2020)
Pertemuan kedua bersama Pak Dai, saya dan mahasiswa lain diminta untuk bisa menjadi orang yang beruntung. Yang dimaksud orang yang beruntung adalah orang yang mampu menjadi pribadi yang lebih baik dibandingkan kemarin. Pak Dai mengingatkan agar kami jangan menjadi orang yang merugi, yaitu orang yang tidak memiliki perkembangan antara hari ini dengan kemarin.
Setelah mendapatkan pelajaran hidup yang berharga, kami diminta untuk mempresentasikan tugas kami yang telah dibuat sebelumnya. Tujuan dari presentasi ini adalah untuk menilai kemampuan mahasiswa dalam pemahaman penggunaan aplikasi OpenModelica.
Materi yang diberikan pada pertemuan ini adalah penggunaan class untuk memanggil sebuah function. Function yang bisa dipanggil beragam jumlahnya, mulai dari penjumlahan sederhana sampai operasi eliminasi matriks.
Di akhir kelas, kami diberi tugas untuk membuat video mengenai cara menyelesaikan persamaan aljabar simultan dengan OpenModelica. Metode yang digunakan menggunakan class untuk memanggil sebuah function, seperti yang sudah diajarkan sebelumnya.
Berikut adalah video yang saya buat:
Pertemuan III (25 November 2020)
Finite Element Method for Trusses
|
Persamaan class Trusses_Tugas3_d29
parameter Integer N=8; //Global matrice = 2*points connected
parameter Real A=0.001; //m^2
parameter Real E=200e9; //Pa
Real G[N,N]; //global
Real Ginitial[N,N]; //global
Real Sol[N]; //global displacement
Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033};
Real R[N]; //global reaction force
Real SolMat[N,1];
Real XMat[N,1];
//boundary condition
Integer b1=1;
Integer b2=3;
//truss 1
parameter Real X1=0; //degree between trusses
Real k1=A*E/1;
Real K1[4,4]; //stiffness matrices
Integer p1a=1;
Integer p1b=2;
Real G1[N,N];
//truss 2
parameter Real X2=0; //degree between trusses
Real k2=A*E/1;
Real K2[4,4]; //stiffness matrices
Integer p2a=2;
Integer p2b=3;
Real G2[N,N];
//truss 3
parameter Real X3=90; //degree between trusses
Real k3=A*E/1.25;
Real K3[4,4]; //stiffness matrices
Integer p3a=2;
Integer p3b=4;
Real G3[N,N];
//truss 4
parameter Real X4=90+38.6598; //degree between trusses
Real k4=A*E/1.6;
Real K4[4,4]; //stiffness matrices
Integer p4a=1;
Integer p4b=4;
Real G4[N,N];
//truss 5
parameter Real X5=90-38.6598; //degree between trusses
Real k5=A*E/1.6;
Real K5[4,4]; //stiffness matrices
Integer p5a=3;
Integer p5b=4;
Real G5[N,N];
/*
for each truss, ensure pXa is lower then pXb (X represents truss element number)
*/
algorithm
//creating global matrice
K1:=Stiffness_Matrices(X1);
G1:=k1*Local_Global(K1,N,p1a,p1b);
K2:=Stiffness_Matrices(X2);
G2:=k2*Local_Global(K2,N,p2a,p2b);
K3:=Stiffness_Matrices(X3);
G3:=k3*Local_Global(K3,N,p3a,p3b);
K4:=Stiffness_Matrices(X4);
G4:=k4*Local_Global(K4,N,p4a,p4b);
K5:=Stiffness_Matrices(X5);
G5:=k5*Local_Global(K5,N,p5a,p5b);
G:=G1+G2+G3+G4+G5;
Ginitial:=G;
//implementing boundary condition
for i in 1:N loop
G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;
end for;
G[2*b1-1,2*b1-1]:=1;
G[2*b1,2*b1]:=1;
G[2*b2-1,2*b2-1]:=1;
G[2*b2,2*b2]:=1;
//solving displacement
Sol:=Gauss_Jordan(N,G,X);
//solving reaction force
SolMat:=matrix(Sol);
XMat:=matrix(X);
R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);
end Trusses_Tugas3_d29;
|