Moh Khairul Imam Assidiqqi

السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ

Profile
Nama Lengkap	Moh Khairul Imam Assidiqqi
NPM	1906301210
Jurusan	Teknik Mesin
Alamat Email	moh.khairul@ui.ac.id

Perkenalan Singkat

Assalamu'alaikum Wr. Wb. Perkenalkan nama saya Moh Khairul Imam Assidiqqi. Saya adalah mahasiswa Departemen Teknik Mesin angkatan 2019.

Pertemuan Pertama Metode Numerik (11-11-2020)

Pada hari Rabu, 11 November 2020 adalah pertemuan pertama kelas Metode Numerik bersama Pak Dr. Ir. Ahmad Indra Siswantara. Pak Dai memberikan penjelasan terlebih dahulu bagaimana cara menggunakan Wiki AIR. Kemudian beliau menjelaskan apa itu metode numerik dan untuk apa kita mempelajarinya.

Ada 4 tujuan mempelajari metode numerik:

1. Memahami konsep dan prinsip dasar di dalam metode numerik.

2. Dapat menerapkan pemahaman terhadap konsep di dalam permodelan numerik.

3. Mampu menerapkan metode numerik di dalam persoalan keteknikan.

4. Mendapat nilai tambah sehingga menjadi orang yang beradab.

Setelah itu Pak Dai menjelaskan secara singkat tentang Open Modelica.

Tugas 1 Metode Numerik

Sebelum kelas berakhir, Pak Dai memberikan kami tugas untuk mempelajari Open Modelica. Setelah itu kami ditugaskan untuk membuat video tutorial cara menggunakan Open Modelica.

Berikut adalah hasil tugas saya:

Pertemuan Kedua Metode Numerik (18-11-2020)

Pada pertemuan kedua dengan Pak Dai, kami diberikan pelajaran yang sangat berharga bahwa kita harus menjadi orang yang beruntung. Maksudnya adalah kita harus menjalani hari ini lebih baik dari hari kemarin. Dan jangan menjadi orang yang merugi yang hari malah lebih buruk dari hari kemarin.

Setelah itu Pak Dai juga menyuruh kami untuk menayangkan tugas-tugas kami pada minggu pertama. Kami diperbolehkan bertanya apapun yang masih kami belum ketahui. Kemudian Pak Dai mengajarkan kami tentang Class dan Function di OpenModelica dan Pak Dai juga mengajarkan bahwa suatu fungsi bisa dipanggil ke sebuah kelas.

Tugas 2 Metode Numerik

Di akhir kelas, Pak Dai memberikan kami tugas untuk membuat video dimana kami diminta untuk membuat sebuah fungsi berupa persamaan aljabar simultan dengan variabel array kemudian membuat class untuk memanggil fungsi tersebut.

Berikut adalah hasil tugas saya:

function

function Gauss
input Real A[5,5];
input Real B[5];
output Real X[5];

algorithm
X:=Modelica.Math.Matrices.solve(A,B);
end Gauss;

class

class SPL_5_Variabel
parameter Real A[5,5]=[2,-2,0,4,2;
                      -2,4,2,0,5;
                      2,-2,2,-2,0;
                      0,4,2,4,4;
                      4,2,2,4,-2];
parameter Real B[5]={2,4,6,8,-12};
Real X[5];

equation
X=Gauss(A,B);                  
end SPL_5_Variabel;

Pertemuan Ketiga Metode Numerik (25-11-2020)

Pada pertemuan ketiga, Pak Dai memaparkan tiga aplikasi metode numerik yang sering digunakan dalam menyelesaikan permasalahan teknik, pertama ada Computation Fluid Dynamics (CFD), lalu Finite Element Analysis, dan Metode Stokastik. Setelah itu Pak Dai meminta beberapa mahasiswa untuk mereview tugas-tugas yang telah diberikan sebelumnya. Salah satu teman kami yaitu Josiah memberikan sharing mengenai aljabar simultan dan variabel array.

Kemudian Pak Dai menjelaskan kembali mengenai metode Gauss. Pak dai mendorong kami untuk membuat code sendiri untuk menyelesaikan Gauss Jordan. Salah satu mahasiswa, yaitu Cristo memberikan sharing mengenai code yang telah ia buat untuk Gauss Jordan, berikut code modelica untuk Gauss Jordan dari Cristo:

// Gauss-Jordan Algorithm
// Transforms input matrix A into reduced row echelon form matrix B
// Christopher S.E. November 2020
input Real [:,:] A;     // An augmented matrix of m*n
output Real [:,:] B;    // Output matrix in reduced row echelon form
// Local variables

protected
Integer h = 1;          // Initialize pivot row
Integer k = 1;          // Initialize pivot column
Integer m = size(A,1);  // Number of rows in matrix
Integer n = size(A,2);  // Number of columns in matrix
Integer c = 0;          // Index counter
Integer max_row;        // Row index of max number in pivot column

Real [:] pivot_column;  // Vector containing pivot column data
Real [:] pivot_row;     // Vector containing backwards pivot row data
Real [:,:] temp_array;  // Stores matrix data when switching rows
Real r;                 // Ratio value used for row operations

// Limit to handle floating point errors
Real float_error = 10e-10;

algorithm

// Transfer input matrix A into variable B
B := A;

while h <= m and k <= n loop
 
// Dealing with floating point errors
for i in 1:m loop
   for j in 1:n loop
     if abs(B[i,j]) <= float_error then
       B[i,j] := 0;
     end if;
   end for;
 end for;

 // Finding the pivot
   pivot_column := {B[i,h] for i in h:m};
 
   // Get position index of lowest row with greatest pivot number
   c:= h-1;
   for element in pivot_column loop
     c := c+1;
     if abs(element) == max(abs(pivot_column)) then
       max_row := c;
     end if;
   end for;
 
 // No pivot in this column, move on to next column
 if B[max_row, k] == 0 then
   k := k+1;
 
 else
   // Swap Rows h <-> max_row
   temp_array := B;
   temp_array[h] := B[max_row];
   temp_array[max_row] := B[h];
   B:= temp_array;
   
   // Divide pivot row by pivot number
   B[h] := B[h]/B[h,k];
   
   // For all rows below the pivot
   for i in (h+1):m loop
     
     // Store the ratio of the row to the pivot
     r := B[i,k] / B[h,k];
     
     // Set lower part of pivot column to zero
     B[i,k] := 0;
     
     // Operations on the remaining row elements
     for j in (k+1):n loop
         B[i,j] := B[i,j] - B[h,j] * r;
     end for;
     
   end for;
   
   // Move on to next pivot row and column
   h := h+1;
   k := k+1;
   
 end if;
 
end while;

// The matrix is now in row echelon form

// Set values of (h,k) to (m,n)
h := m;
k := n;

while h >= 1 and k >=1 loop

 // Dealing with floating point errors
 for i in 1:m loop
   for j in 1:n loop
     if abs(B[i,j]) <= float_error then
       B[i,j] := 0;
     end if;
   end for;
 end for;

 // Finding the pivot
   pivot_row := {B[h,i] for i in 1:k};
   
   // Get position index k of pivot
   c := 0;
   for element in pivot_row loop
     c := c+1;
     if element <> 0 then
       break;
     end if;
   end for;
   k := c;

 // No pivot in this row, move on to next row
 if B[h, k] == 0 then
   h := h-1;
   
 else
   
   // Perform row operations
   for i in 1:(h-1) loop
     r := B[i,k];
     B[i] := B[i] - B[h] * r;
   end for;
   
   // Move on to next pivot row and column
   h := h-1;
   k := k-1;
   
 end if;

end while;

// The matrix is now in reduced row echelon form

end GaussJordan;

Tugas 3 Metode Numerik

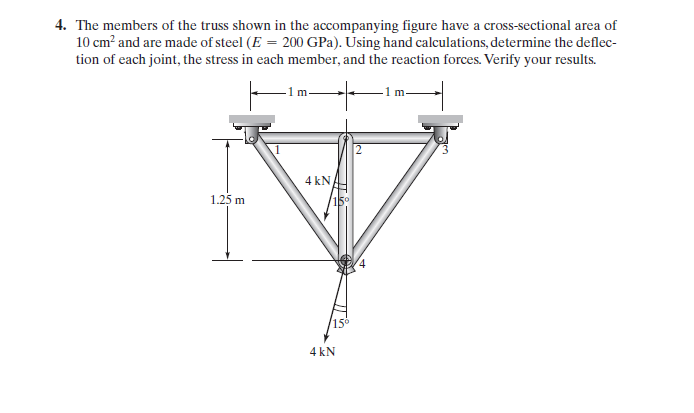
Di akhir kelas, Pak Dai memberikan kami tugas yaitu menyelesaikan persoalan berikut:

Berikut adalah penyelesaiannya:

<syntaxhighlight lang="modelica">

• class Trusses

parameter Integer N=8; //Global matrice = 2*points connected parameter Real A=0.001; //Area m2 parameter Real E=200e9; //Pa Real G[N,N]; //global Real Ginitial[N,N]; //global Real Sol[N]; //global dispplacement Real X[N]={0,0,-1035.2762,-3863.7033,0,0,-1035.2762,-3863.7033}; Real R[N]; //global reaction force Real SolMat[N,1]; Real XMat[N,1];

//boundary condition Integer b1=1; Integer b2=3;

//truss 1 parameter Real X1=0; //degree between truss Real k1=A*E/1; Real K1[4,4]; //stiffness matrice Integer p1a=1; Integer p1b=2; Real G1[N,N];

//truss 2 parameter Real X2=0; //degree between truss Real k2=A*E/1; Real K2[4,4]; //stiffness matrice Integer p2a=2; Integer p2b=3; Real G2[N,N];

//truss 3 parameter Real X3=90; //degree between truss Real k3=A*E/1.25; Real K3[4,4]; //stiffness matrice Integer p3a=2; Integer p3b=4; Real G3[N,N];

//truss 4 parameter Real X4=90+38.6598; //degree between truss Real k4=A*E/1.6; Real K4[4,4]; //stiffness matrice Integer p4a=1; Integer p4b=4; Real G4[N,N];

//truss 5 parameter Real X5=90-38.6598; //degree between truss Real k5=A*E/1.6; Real K5[4,4]; //stiffness matrice Integer p5a=3; Integer p5b=4; Real G5[N,N];

/* for each truss, please ensure pXa is lower then pXb (X represents truss element number)

• /

algorithm

//creating global matrice K1:=Stiffness_Matrices(X1); G1:=k1*Local_Global(K1,N,p1a,p1b);

K2:=Stiffness_Matrices(X2); G2:=k2*Local_Global(K2,N,p2a,p2b);

K3:=Stiffness_Matrices(X3); G3:=k3*Local_Global(K3,N,p3a,p3b);

K4:=Stiffness_Matrices(X4); G4:=k4*Local_Global(K4,N,p4a,p4b);

K5:=Stiffness_Matrices(X5); G5:=k5*Local_Global(K5,N,p5a,p5b);

G:=G1+G2+G3+G4+G5; Ginitial:=G;

//implementing boundary condition for i in 1:N loop

G[2*b1-1,i]:=0;
G[2*b1,i]:=0;
G[2*b2-1,i]:=0;
G[2*b2,i]:=0;

end for;

G[2*b1-1,2*b1-1]:=1; G[2*b1,2*b1]:=1; G[2*b2-1,2*b2-1]:=1; G[2*b2,2*b2]:=1;

//solving displacement Sol:=Gauss_Jordan(N,G,X);

//solving reaction force SolMat:=matrix(Sol); XMat:=matrix(X); R:=Reaction_Trusses(N,Ginitial,SolMat,XMat);

end Trusses;