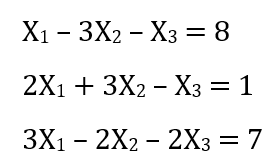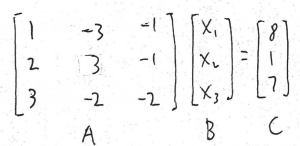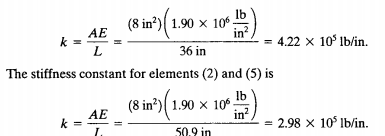Difference between revisions of "Metnum03 Favian Adyatma"
(→Pertemuan 3: 23 November 2020) |
(→Pertemuan 3: 23 November 2020) |
||
| Line 342: | Line 342: | ||
6. Mencari solusi (OpenModelica) | 6. Mencari solusi (OpenModelica) | ||
| − | Tahap pencarian solusi inilah yang akan digunakan aplikasi OpenModelica | + | Tahap pencarian solusi inilah yang akan digunakan aplikasi OpenModelica. ''Input'' yang dilakukan pada aplikasi OpenModelica adalah seperti berikut. |
| + | |||
| + | [[File:Simulasimodelicavian.PNG|550px]] | ||
| + | |||
| + | Ketika saya menggunakan fitur simulate, maka hasilnya akan digambarkan seperti ini. | ||
| + | |||
| + | [[File:Hasilvianbeam.png|550px]] | ||
| + | |||
| + | 7. Memperoleh besaran gaya-gaya | ||
Revision as of 13:00, 30 November 2020
Assalamualaikum Wr. Wb.
Salam sejahtera untuk kita semua. Semoga kita semua selalu dalam lindungan Tuhan Yang Maha Esa.
Nama: Favian AdyatmaNPM: 1806181773
Mata Kuliah: Metode Numerik 03 (TA 2020/2021 Ganjil)
Pertemuan 1: 9 November 2020
Pertemuan perdana kelas Metnum 03 merupakan pengenalan terhadap mata kuliah Metode Numerik. Kami membahas mulai dari akarnya dan kaitannya terhadap kehidupan kita sehari-hari, seperti proses berpikir dan aplikasinya terhadap device yang digunakan pada kehidupan sehari-sehari. Pada akhir kelas, kami diberikan tugas untuk memasukkan laporan mengenai hasil belajar pada akun masing-masing kita di air.eng.ui.ac.id, yaitu proses kami mempelajari software Open Modelica yang dapat diunduh melalui jejaring openmodelica.org dan menceritakan proses pembelajaran sebelum UTS.
Proses Pembelajaran Sebelum UTS
Sebelum UTS, kami mempelajari beberapa bab Metode Numerik dengan dosen Pak Engkos, yaitu sebagai berikut:
- Turunan Numerik
Turunan numerik dibagi menjadi tiga pendekatan, yaitu turunan mundur, turunan maju, dan turunan pusat. Berikut adalah prakteknya dalam Microsoft Excel.
- Pencarian Akar secara Numerik
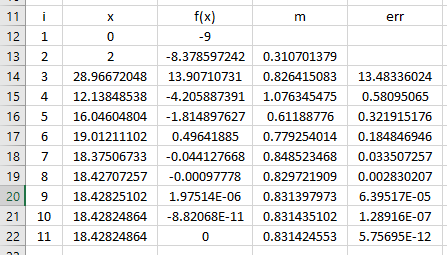
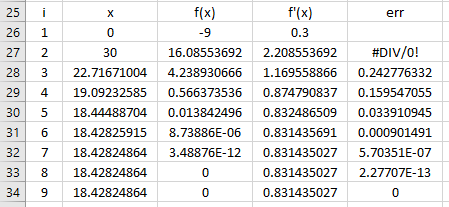
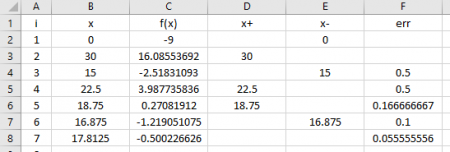
Pencarian akar ini bisa dilakukan dengan dua metode, yaitu Bracketing Method dan Open Method. Bracketing Method terdiri dari metode Bisecant, Graphical, dan False Position, sedangkan Open Method terdiri dari Newton-Raphson, Secant, dan Sample Fix Point. Di bawah ini akan saya sertakan tangkapan layar dari hasil pencarian akar di Excel dari metode Bisecat, Secant, dan Newton Raphson.
- Materi lainnya
Ada beberapa materi lainnya yang sempat dipelajari pada kelas Metode Numetik 03, antara penjabaran iterasi sin x dan cos x secara numerik dan praktik metode numerik pada alat-alat tertentu.
Open Modelica
Tugas berikutnya adalah merekap hasil pembelajaran aplikasi Open Modelica. Mengenai hal tersebut, hambatan yang ada sangat terasa karena saya tidak dapat mengunggah perangkat lunak tersebut disebabkan oleh network issue yang terjadi pada proses pengunggahannya. Akibatnya software tersebut gagal diunggah. Kedepannya saya akan menanyakan kepada teman-teman mengenai masalah tersebut. Namun, pembelajaran tetap saya lakukan dengan meriset situs openmodelica.org dan mencari tahu kegunaan dari aplikasi ini. Salah satu referensi yang saya gunakan adalah melalui YouTube dengan tautan berikut:
Open Modelica merupakan perangkat lunak yang digunakan untuk mempermudah simulasi permodelan metode numerik. Seperti CFDSOF-NG yang menjadi alat untuk simulasi aliran fluida, aplikasi ini adalah alat untuk simulasi metode numerik. Selain itu, dapat dipraktekkan pula pengendalian sistem dengan meng-input rangkaian yang biasa dilakukan saat proses pengendalian sistem baik elektronik maupun mekanik. Open Modelica juga seringkali digunakan pada industri yang membutuhkan kinerja pengendalian sistem didalamnya.
Pertemuan 2: 16 November 2020
Tugas 2
Sebelum kegiatan kelas kedua (evaluasi hasil belajar kami tentang yang sudah kami pelajari tentang Metode Numerik sebelum UTS) berakhir, Pak Dai memberikan tugas mengenai simulasi perhitungan aljabar di Aplikasi OpenModelica. Kami diminta melaksanakan simulasi tersebut dengan menyelesaikan persamaan aljabar dan coding sederhana terkait nilai rata-rata sepuluh sampel. Maka saya mengambil tiga buah persamaan untuk diselesaikan, yaitu:
Aljabar tersebut dapat diselesaikan melalui OpenModelica yang telah terunggah pada gawai masing-masing mahasiswa. Pertama-tama, saya melakukan input pada aplikasi OpenModelica, dimana A dan C adalah input sedangkan B adalah faktor dari x1, x2, dan x3 yang akan dicari. Gambaran itu dapat disederhanakan dengan ilustrasi berikut.
Maka, pada simulasi OpenModelica ini, saya meng-input data A dan C seperti pada gambar berikut.
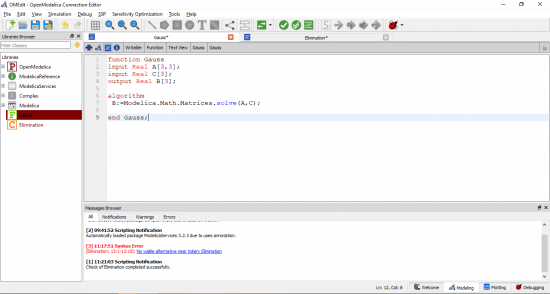
Pada gambar tersebut, A dituliskan sebagai A[3,3] yang artinya merupakan matriks 3x3. Kemudian, input C adalah matriks 3x1, maka ditulis C[3], dan yang terakhir adalah output, yakni nilai yang dicari, matriks B, yang merupakan matriks 3x1. Ketiga data tersebut disimpan pada fitur Function dengan nama "Gauss".
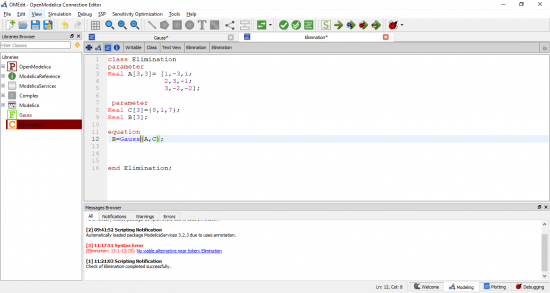
Setelah itu, untuk dapat mendapatkan hasil yang diinginkan, saya memasukkan matriks pada fitur Class dengan nama "Elimination". Pada fitur itu, nilai-nilai pada matriks dimasukkan menjadi coding sederhana seperti gambar berikut.
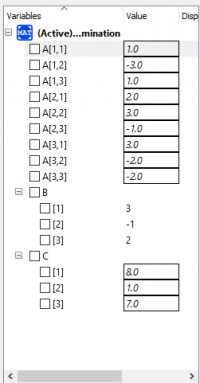
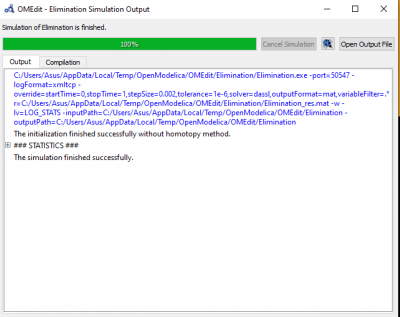
Tahap berikutnya adalah menjalankan formula dan data yang telah di-input dengan menklik fitur Simulate. Ketika sudah selesai, maka kita akan mendapatkan jawaban dari persamaan yang diinginkan. Hasil dari simulasi yang saya lakukan dapat dilihat melalui gambar di bawah ini.
Dapat disimpulkan bahwa jawaban dari persamaan yang di-input adalah x1=3, x2=-1, dan x3=2.
Sebagai bahan kelengkapan dari hasil simulasi OpenModelica ini, saya menyertakan Elimination Simulation Output dari simulasi ini.
Pertemuan 3: 23 November 2020
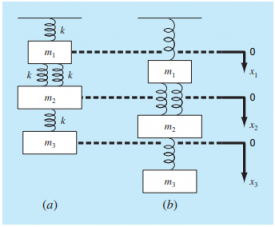
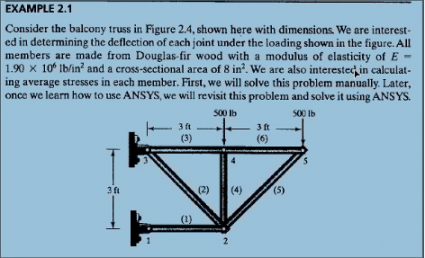
Kelas ketiga, tanggal 23 November 2020, kegiatan diawali dengan diskusi buku bab 12 (hal. 328) mengenai displacement pegas massa. Di bawah ini saya unggah foto dari buku textbook MK. Metoda Numerik tersebut.
Berangkat dari gambar tersebut, kami dipersilakan untuk membaca terlebih dahulu sebelum diskusi dimulai. Diskusi diawali dengan penjelasan peristiwa yang terjadi jika sebuah benda diberikan displacement. Melalui itu juga kami meneruskan pembahasan mengenai persamaannya.
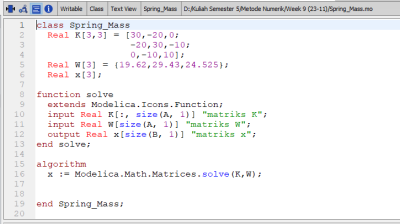
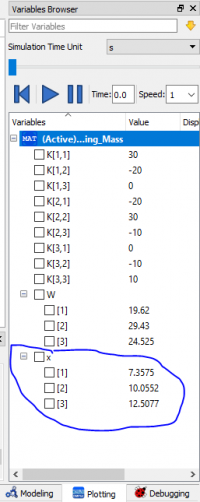
Sesi kelas dilanjutkan dengan sesi tanya jawab satu per satu mahasiswa oleh dosen Pak Dai. Kami menjelaskan mengenai progres pembelajaran kami di website air.eng.ui.ac.id. Namun, saya belum dapat kesempatan untuk menjelaskan progres pembelajaran saya. Sembari melakukan tanya jawab satu per satu, kami juga melakukan simulasi mengenai displacement dari suatu persoalan pegas massa yang terdapat pada textbook Metode Numerik halaman 330. Berikut gambaran dan penyelesaian simulasinya pada aplikasi OpenModelica.
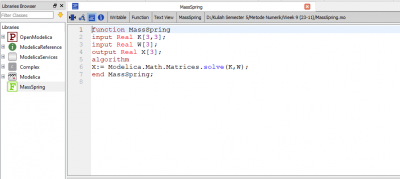
Tidak berbeda jauh dari PR yang sudah diberikan sebelumnya, tahap awal simulasi dilakukan dengan meng-input data yang tersedia dan dikemas dalam bentuk matriks. Hal tersebut tercermin pada gambar di atas, dimana matriks K adalah matriks 3x3 dan matriks W (3x1) dengan nilainya yang sudah tertulis, serta matriks X (3x1) yang kita cari.
Melalui fitur Function, seperti yang digambar di atas, maka matriks yang dicari dapat ditentukan. Gambar di bawah ini adalah jawaban dari matriks yang ingin dicari.
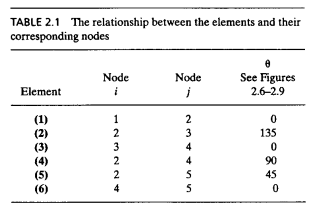
Sesaat sebelum kelas selesai, seperti biasa, kami diberikan tugas untuk mengerjakan soal tentang statika struktur dan disimulasikan pada OpenModelica. Berikut adalah gambar dari soal yang diberikan sebagai tugas kepada peserta didik kelas Metode Numerik 03.
Tugas 3
Melalui referensi yang saya gunakan, yaitu solusi dari buku terkait, soal tersebut dijawab dengan beberapa tahapan. Tahapan-tahapannya adalah sebagai berikut:
1. Mengubah permasalahan menjadi noda dan elemen
Mengubah soal statika struktur di atas menjadi noda dan elemen digambarkan dengan tabel berikut ini.
2. Tahap berikutnya adalah membuat asumsi solusi yang mendekati sifat elemen
Pada tahap ini kami menentukan asumsi untuk mendapatkan properties dari beam, yaitu k dengan rumus (AE)/L. L pada beam 1, 3, 4, dan 6 adalah 3 ft atau 36 inchi dan beam 2, 5 adalah 50.9 inchi (3 akar 2 ft)
3. Mengembangkan persamaan untuk menyelesaikan persamaan tiap elemen
Setiap elemen akan dianalisis berdasarkan posisi dan gaya reaksi yang terjadi pada elemennya. Analisis akan dimanifestasikand alam bentuk matriks. Berikut hasil analisis dari elemen beam-nya
- Elemen 1, 3, dan 6
- Elemen 4
- Elemen 2 dan 5
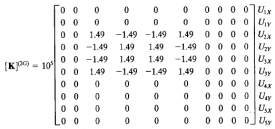
4. Penggabungan matriks
Setelah di atas kita melakukan analisis per golongan elemen, maka berikutnya adalah melakukan penggabungan matriks. Di bawah ini adalah hasil dari penggabungan tersebut.
5. Menentukan boundary condition
Berdasarkan solusi dari referensi yang ada, ditentukan beberapa kondisi batas:
U1(x)=U1(y)=U3(x)=U3(y)=0
F4(y) = -500 lb dan F5(y) = -500 lb
Dengan memasukkannya ke dalam matriks, maka menjadi:
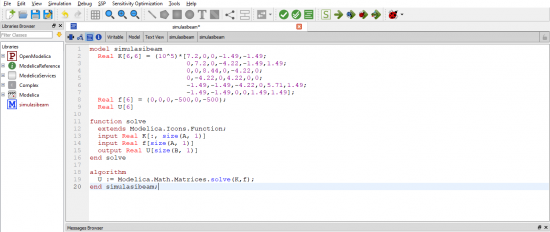
6. Mencari solusi (OpenModelica)
Tahap pencarian solusi inilah yang akan digunakan aplikasi OpenModelica. Input yang dilakukan pada aplikasi OpenModelica adalah seperti berikut.
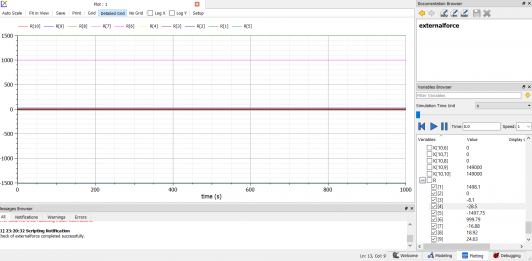
Ketika saya menggunakan fitur simulate, maka hasilnya akan digambarkan seperti ini.
7. Memperoleh besaran gaya-gaya