Difference between revisions of "Metnum03-Farhan Aditya Wibowo"
(→Pertemuan 3 ( 23 November 2020)) |
(→Pertemuan 3 ( 23 November 2020)) |
||
| Line 39: | Line 39: | ||
[[File:Tugasmetnumbowo5.png]] | [[File:Tugasmetnumbowo5.png]] | ||
| + | |||
| + | == Pertemuan 3 example 2.1(23 November 2020) == | ||
| + | Di pertemuan hari ini, Pak Dai menjelaskan tentang aplikasi metode numerik untuk permasalahan-permasalahan teknik. Salah satunya adalah permasalahan sistem pegas-massa. | ||
| + | |||
| + | Setelah kelas, Pak Dai memberikan tugas untuk menyelesaikan soal berikut: | ||
| + | |||
| + | [[File:Tugasmetnumbowo6.png]] | ||
| + | |||
| + | Untuk menyelesaikan soal ini perlu dilakukan pengelompokan menjadi node dan elemen seperti pada tabel berikut: | ||
| + | |||
| + | [[File:Tugasmetnumbowo7.png]] | ||
| + | |||
| + | lalu perlu dilakukan perhitungan nilai kekakuan pada elemen. Untuk elemen 1,3,5, dan 6 nilai kekakuannya adalah 4,22 x 10^5 lb/in. sedangkan untuk elemen 2, dan 4 nilai kekakuannya adalah 2,98 x 10^5 lb/in. | ||
| + | |||
| + | setelah itu perlu dilakukan analisis kekakuan pada tiap elemen dalam matriks koordinat global, kemudian dijumlahkan untuk mendapatkan K global. berikut adalah hasil penjumlahan dari nilai kekakuan tiap elemen: | ||
| + | |||
| + | [[File:Tugasmetnumbowo8.png]] | ||
| + | |||
| + | disederhanakan menjadi | ||
| + | |||
| + | [[File:Tugasmetnumbowo9.png]] | ||
| + | |||
| + | setelah mendapat matriks kekakuan, diterapkan kondisi batas dan beban. Untuk node 1 dan 3 adalah fixed, maka U1X=0, U1Y=0, U3X=0, U3Y=0 dan beban diberikan pada node 4 dan 5 sebesar F4Y= -500lb dan F5Y= -500lb | ||
| + | |||
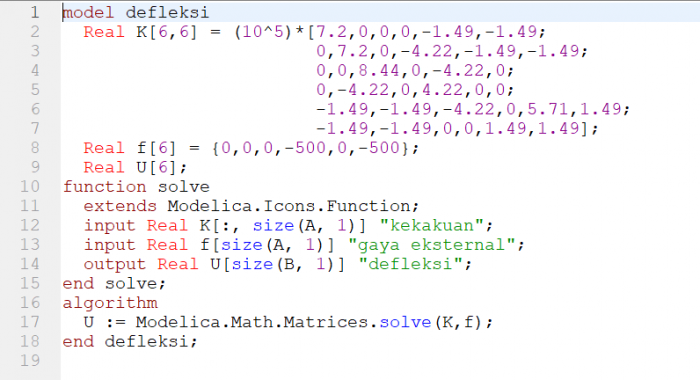
| + | dengan menggunakan Hukum Hooke yaitu F=k.x, maka didapatkan persamaan defleksi menjadi | ||
| + | |||
| + | [[File:Tugasmetnumbowo10.png]] | ||
| + | |||
| + | Persamaan diatas kemudian diselesaikan dengan OpenModelica, berikut saya lampirkan coding yang saya buat | ||
| + | |||
| + | [[File:Tugasmetnumbowo11.png]] | ||
| + | |||
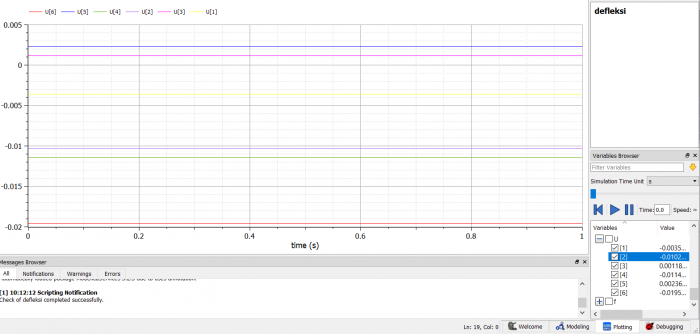
| + | setelah melakukan pengecekan dan simulasi, saya melakukan plotting. berikut hasil plotting simulasi tersebut. | ||
| + | |||
| + | [[File:Tugasmetnumbowo12.png]] | ||
| + | |||
| + | hasil dapat dilihat pada panel di bagian kanan bawah gambar. | ||
| + | |||
| + | |||
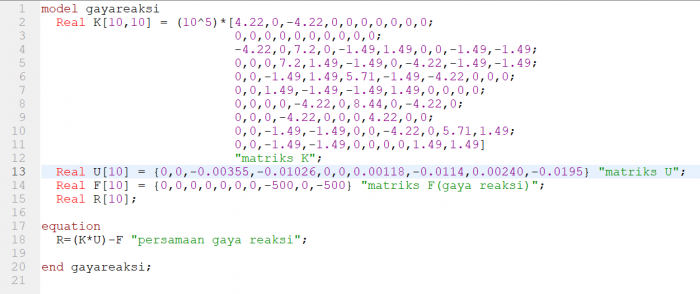
| + | Untuk mendapatkan gaya reaksi, persamaannya adalah: | ||
| + | |||
| + | {R}=[K].{U}-{F} | ||
| + | |||
| + | diterapkan matriks-matriks yang sudah diketahui, didapat: | ||
| + | |||
| + | [[File:Tugasmetnumbowo13.png]] | ||
| + | |||
| + | Persamaan diatas dapat diselesaikan oleh openmodelica. berikut adalah coding yang saya buat | ||
| + | |||
| + | [[File:Tugasmetnumbowo14.png]] | ||
| + | |||
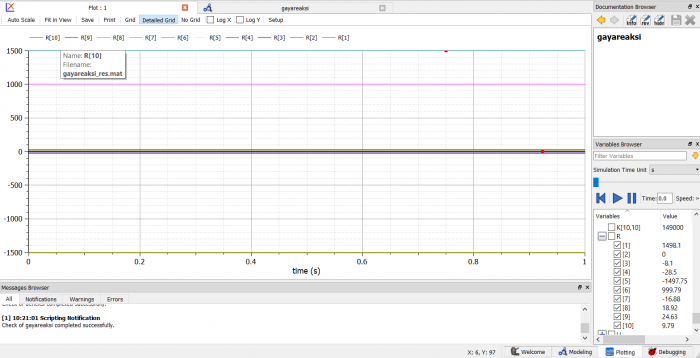
| + | hasil simulasi tersebut di plot sebagai berikut: | ||
| + | |||
| + | [[File:Tugasmetnumbowo15.png]] | ||
| + | |||
| + | nilai R tiap node dapat dilihat di bagian kanan bawah gambar | ||
Revision as of 12:01, 30 November 2020
بِسْمِ اللَّهِ الرَّحْمَنِ الرَّحِيم
dengan ini saya mengisi halaman ini untuk memenuhi mata kuliah metode numerik
Contents
Bio Data
Nama : Farhan Aditya Wibowo
NPM : 1706024665
Program Studi : S1 Teknik Mesin Parallel
Pertemuan 1 (19 November 2020)
Pada kesempatan pertemuan sebelumnya kelas kami diberikan fasilitas untuk berdiskusi untuk membahas hal apa saja yang telah didapat dari kelas metode numerik dan pengaplikasian dari yang telah didapat, dari situ saya meraskan bahwa pada kehidupan sehari-hari kitapun harus ada suatu target seperti layaknya kita mengerjakan metode numerik dengan target tugas selesai dan mengerti apa yang di beri tahu oleh orang yang lebih berpengalaman dalam bidang tersebut. Lalu selanjutnya kami membahas tentang konsep tak hingga yang sebenarnya bukan bilangan, melainkan hanya sebuah konsep dibuat manusia karena manusia memiliki batasan dan hanya maha penciptalah yang tahu akan tak hingga tersebut. Pada sesi selanjutnya kami diberi informasi bahwa pemberian materi akan berupa perangkat lunak Open Modelica. Open Modelica merupakan penyimulasi sistem dengan data input kode untuk melakukan suatu penelitian terhadap sistem tersebut.
Pertemuan 2 (16 November 2020)
Membuat suatu program untuk menyelesaikan persamaan aljabar simultan, berikut merupakan program yang saya buat:
Dengan metode gauss elimination dan function solve yang disediakan oleh software modelica, saya mendapatkan hasil seperti berikut :
Pertemuan 3 ( 23 November 2020)
Pada pertemuan ini kami membuktikan studi dari buku Numerical Methods for Engineers 7th Edition
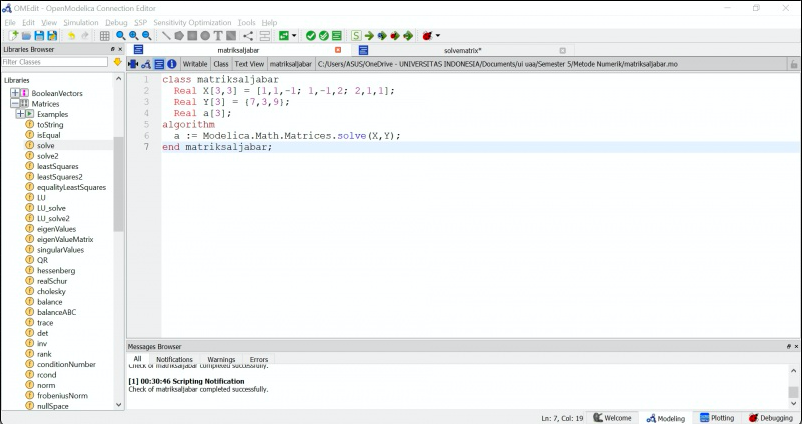
dari soal diketahui matriks [K][X]=[W]
komponen [K] dan [W] diketahui, lalu mencari komponen [X]
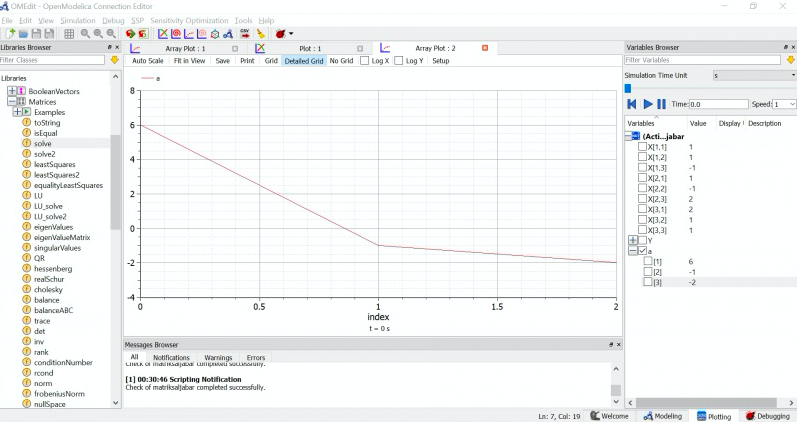
Pada Open Modelica saya menggunakan metode Gauss Elimination karena pada cara manual kita seharusnya mencari variable dari Matrik K dan W.
dengan begitu ini hasil dari yang saya kerjakan
Pertemuan 3 example 2.1(23 November 2020)
Di pertemuan hari ini, Pak Dai menjelaskan tentang aplikasi metode numerik untuk permasalahan-permasalahan teknik. Salah satunya adalah permasalahan sistem pegas-massa.
Setelah kelas, Pak Dai memberikan tugas untuk menyelesaikan soal berikut:
Untuk menyelesaikan soal ini perlu dilakukan pengelompokan menjadi node dan elemen seperti pada tabel berikut:
lalu perlu dilakukan perhitungan nilai kekakuan pada elemen. Untuk elemen 1,3,5, dan 6 nilai kekakuannya adalah 4,22 x 10^5 lb/in. sedangkan untuk elemen 2, dan 4 nilai kekakuannya adalah 2,98 x 10^5 lb/in.
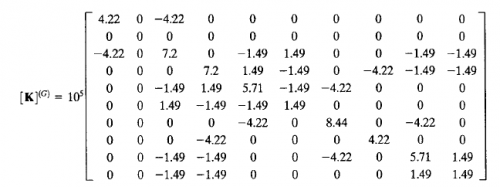
setelah itu perlu dilakukan analisis kekakuan pada tiap elemen dalam matriks koordinat global, kemudian dijumlahkan untuk mendapatkan K global. berikut adalah hasil penjumlahan dari nilai kekakuan tiap elemen:
disederhanakan menjadi
setelah mendapat matriks kekakuan, diterapkan kondisi batas dan beban. Untuk node 1 dan 3 adalah fixed, maka U1X=0, U1Y=0, U3X=0, U3Y=0 dan beban diberikan pada node 4 dan 5 sebesar F4Y= -500lb dan F5Y= -500lb
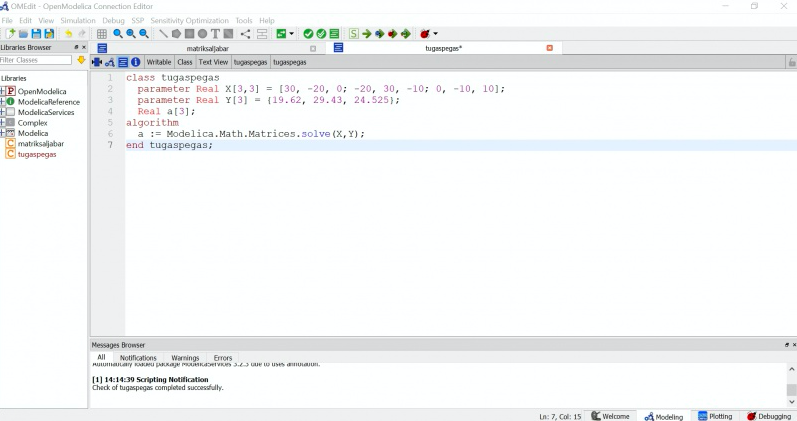
dengan menggunakan Hukum Hooke yaitu F=k.x, maka didapatkan persamaan defleksi menjadi
Persamaan diatas kemudian diselesaikan dengan OpenModelica, berikut saya lampirkan coding yang saya buat
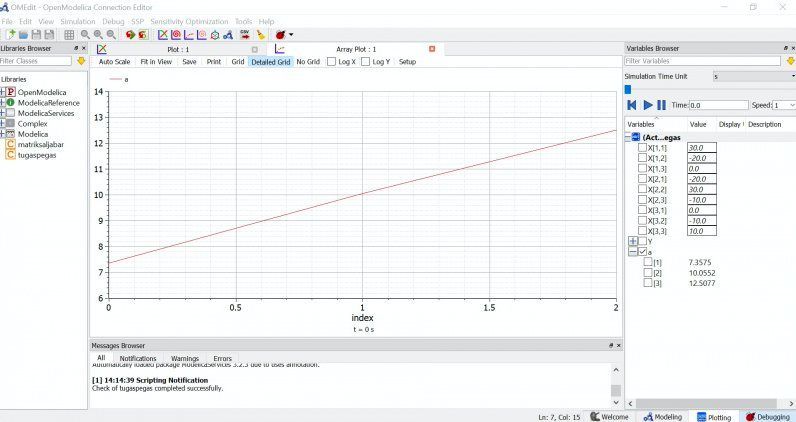
setelah melakukan pengecekan dan simulasi, saya melakukan plotting. berikut hasil plotting simulasi tersebut.
hasil dapat dilihat pada panel di bagian kanan bawah gambar.
Untuk mendapatkan gaya reaksi, persamaannya adalah:
{R}=[K].{U}-{F}
diterapkan matriks-matriks yang sudah diketahui, didapat:
Persamaan diatas dapat diselesaikan oleh openmodelica. berikut adalah coding yang saya buat
hasil simulasi tersebut di plot sebagai berikut:
nilai R tiap node dapat dilihat di bagian kanan bawah gambar