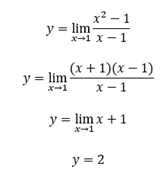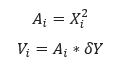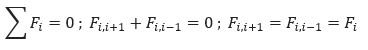Difference between revisions of "Aji Putro Prakoso"
(→Optimasi Biaya Pembangunan Rumah) |
(→Optimasi Biaya Pembangunan Rumah) |
||
| Line 124: | Line 124: | ||
[[File:aji-t3-g1.jpg]] | [[File:aji-t3-g1.jpg]] | ||
| − | Luas bangunan yang dipatok 72 m2 menjadi constrain pertama dimana (A + B + C + D + E) X (F + G + H) = 72. Selanjutnya, berdasarkan pengalaman, sebuah car port paling tidak berukuran 3m x 4m. Sehingga menjadi constrain H = 4. Kemudian, ditetapkan pula paling tidak sebuah kamar memiliki luas 8 m2, dengan lebar tidak kuran dari 2 meter. Sehingga constrain selanjutnya adalah C x F = D x F = E x F = 8, selain itu, C = D = E, dengan 2 < C < 4, dan 2 < F < 4. Untuk kamar mandi ditetapkan berukuran 2x3m, sehingga B = 1.5. Untuk dapur yang berada di sebelah kamar mandi, paling tidak ada ruang untuk menaruh kompor sekitar 1 meter, sehingga 1 < A < 2.5. Agar seseorang dapat masuk kamar E,F, maka harus ada gap antara kamar E,F dengan car port, paling tidak 1m, sehingga ditetapkan G = 1 Setelah masing-masing constrain ditetapkan, dilakukan simulasi dasar apakah setiap constrain tidak saling bentrok, digunakan nilai minimum untuk A, B, C, D, dan E, yaitu, 1.5, 1, 2, 2, 2, sehingga lebar rumah minimal adalah 8,5 meter, padahal untuk car port dan kamar E,F saja paling tidak membutuhkan 8 meter, sehingga rancangan pertama sangat sulit untuk dilaksanakan. Langkah selanjutnya untuk memperbaiki rancangan adalah pengetatan constrain dan pembuatan | + | Luas bangunan yang dipatok 72 m2 menjadi constrain pertama dimana (A + B + C + D + E) X (F + G + H) = 72. Selanjutnya, berdasarkan pengalaman, sebuah car port paling tidak berukuran 3m x 4m. Sehingga menjadi constrain H = 4. Kemudian, ditetapkan pula paling tidak sebuah kamar memiliki luas 8 m2, dengan lebar tidak kuran dari 2 meter. Sehingga constrain selanjutnya adalah C x F = D x F = E x F = 8, selain itu, C = D = E, dengan 2 < C < 4, dan 2 < F < 4. Untuk kamar mandi ditetapkan berukuran 2x3m, sehingga B = 1.5. Untuk dapur yang berada di sebelah kamar mandi, paling tidak ada ruang untuk menaruh kompor sekitar 1 meter, sehingga 1 < A < 2.5. Agar seseorang dapat masuk kamar E,F, maka harus ada gap antara kamar E,F dengan car port, paling tidak 1m, sehingga ditetapkan G = 1 Setelah masing-masing constrain ditetapkan, dilakukan simulasi dasar apakah setiap constrain tidak saling bentrok, digunakan nilai minimum untuk A, B, C, D, dan E, yaitu, 1.5, 1, 2, 2, 2, sehingga lebar rumah minimal adalah 8,5 meter, padahal untuk car port dan kamar E,F saja paling tidak membutuhkan 8 meter, sehingga rancangan pertama sangat sulit untuk dilaksanakan. Langkah selanjutnya untuk memperbaiki rancangan adalah pengetatan constrain dan pembuatan sketsa baru. |
| + | |||
| + | Berikut adalah rancangan sketsa rumah setelah direvisi. | ||
---- | ---- | ||
Revision as of 00:01, 9 March 2019
Resume diskusi kelas tgl 4/2/2019 “Pengantar Komputasi Teknik”
Akal dan Kebenaran
Pertemuan pertama kelas komputasi teknik dimulai dengan pengantar tentang komputasi teknik. Sebagai pengantar, ditekankan bahwa syarat mahasiswa yang dapat mengikuti kelas komputasi teknik adalah mahasiswa yang menggunakan akalnya, tidak hanya dengan persepsi. Maksudnya adalah, pada mata kuliah ini, sesuatu dianggap benar apabila sejalan dengan logika, dapat diverifikasi melalui hukum-hukum (rumus-rumus/persamaan-persamaan) yang diakui kebenarannya, atau divalidasi dengan kondisi yang terjadi, tidak menyimpulkan hanya dari apa yang dirasakan oleh pancaindra, atau anggapan seseorang yang dianggap pasti benar (Taklid).
Kebenaran dapat menjadi relatif jika dilihat dari satu sudut pandang. Misalnya, ketika kita pergi dari Jakarta ke Bandung, maka orang di Jakarta menganggap kita pergi, di sisi lain, orang di Bandung menganggap kita datang. Oleh karena itu diperlukan frame of reference atau titik referensi atau base point (titik basis) untuk mendapatkan kesepahaman atau pemahaman yang sama, sehingga, pada kasus ini, pemahaman orang di Jakarta dan Bandung akan sama, bahwa memang kita sedang pergi dari Jakarta ke Bandung. Selain itu, kebenaran juga dapat relatif terhadap waktu, hukum gaya Newton yang berbunyi F = m*a kini direvisi oleh hukum relativitas Einstein yang berbunyi E=m*c2 , hal ini menunjukkan, seiring kemajuan manusia, pengetahuan terus berkembang, dan kebenaran dapat direvisi seiring berjalannya waktu. Lagi-lagi kesepakatan dan common understanding menjadi penting untuk memperoleh kebenaran. Namun demikian, kita harus tetap yakin bahwa kebenaran yang hakiki adalah apa yang terdapat pada Al-Quran yang tidak akan direvisi. Kenyataannya, apa-apa yang dulu dianggap benar namun bertentangan dengan Al-Quran kini direvisi dan apa yang terdapat dalam Al-Quran lah yang benar. Selain itu, sebagai Warga Negara Indonesia, kita juga telah bersepakat bahwa Pancasila adalah sebuah kebenaran yang tidak dapat direvisi.
Berdasarkan pengalaman dan apa yang telah dipelajari Pak DAI, beliau menyimpulkan terdapat 4 hal yang menghalangi manusia dari kebenaran, yaitu: 1. Kehormatan/kedudukan, 2. Materi, baik harta maupun pengetahuan, 3. Ikut-ikutan, atau taklid pada orang-orang tertentu, 4. Berbuat maksiat.
Definisi dan Tujuan
Mata kuliah komputasi teknik didefinisikan sebagai cara untuk memahami respons sebuah sistem mekanik yang kompleks jika diberi beban dengan menggunakan pendekatan komputasi, salah satunya finite element maupun finite volume. Beban di sini dapat berarti sebuah beban yang sekali datang, beban kejut, maupun beban gradual terus menerus. Sebuah benda yang diam atau tidak mengalami percepatan pun bisa jadi mengalami beban. Respons sesuatu terhadap beban sendiri sesungguhnya tidak linier, rumus-rumus eksak yang ada kebanyakan merupakan linearisasi dari kondisi sesungguhnya yang belum tentu selalu benar. Mata kuliah komputasi teknik membahas metode lain memecahkan masalah-masalah yang sesungguhnya tidak dapat dihitung menggunakan cara eksak yang cenderung linier. Namun demikian, metode ini pun memiliki batasan, yaitu seluruh perhitungan dianggap sesuatu yang berhingga dan berdigit (finite), padahal kuasa Tuhan menciptakan alam semesta adalah tak berhingga, atau infinite.
Ciptaan Tuhan yang infinite atau tak berhingga sendiri dapat didefinisikan menjadi dua arah, ke luar dan ke dalam. Ciptaan Tuhan yang tak berhingga ke luar, maksudnya adalah bahwa kita sebenarnya belum tahu seberapa jauh batas alam semesta ini. Kita juga tidak pernah tahu bagaimana kondisi 0 K, atau kondisi temperatur tak berhingga. Di sisi lain, ciptaan Tuhan tak berhingga ke dalam, maksudnya adalah, sebuah balok yang panjangnya 1 meter dapat dibagi menjadi 1000 bagian, kemudian seharusnya dapat pula dibagi menjadi 1’000’000 bagian, dan seharusnya dapat dibagi lagi hingga tak berhingga. Neutron pun kini dapat dibagi menjadi beberapa bagian, dan seterusnya, dan seterusnya. Karena keterbatasan kemampuan kita menghitung, maka setiap masalah yang diperhitungkan dengan metode komputasi harus dibatasi dengan sesuatu yang finite atau berhingga, baik dalam hal jangkauan perhitungan, maupun ketelitian perhitungannya. Setelah mengikuti mata kuliah komputasi teknik, mahasiswa diharapkan memenuhi dua kriteria yang ditetapkan, yaitu:
1. Memahami konsep aritmatika, flow-chart, dan matematika,
2. Menjadi lebih tahu siapa dirinya.
Contoh kasus perbedaan metode eksak dengan komputasi
Untuk meningkatkan pemahaman mahasiswa terkait perbedaan metode eksak dengan komputasi, Pak DAI memberikan sebuah contoh kasus soal matematika sebagai berikut:
Soal tersebut tidak dapat dikerjakan langsung karena apabila dimasukkan x=1, maka penyebutnya menjadi 0 dan y menjadi tidak dapat didefinisikan.
Dengan menggunakan metode eksak, kasus ini dapat diselesaikan menggunakan pendekatan limit, melalui pendekatan ini, sebuah persamaan kompleks pada kasus tertentu dapat diuraikan dan diselesaikan secara aritmatis seperti contoh berikut ini.
Sedangkan, dengan metode komputasi, kasus ini dapat diselesaikan dengan metode iteratif. Metode ini menggunakan pendekatan dari sebuah nilai x dengan nilai yang di atas atau di bawahnya sedekat mungkin, seperti tabel berikut.
Pemodelan (Modelling)
Definisi Pemodelan dan Pemodelan Menggunakan Akal
Pemodelan adalah penyederhanaan sesuatu dari yang sesungguhnya, namun seakan-akan itu adalah hal yang sesungguhnya. Sebelum mempelajari lebih lanjut terkait pemodelan, kita perlu mundur kembali sedikit tentang persepsi. Karena yang sedang dipelajari adalah ilmu mekanika, maka seluruh hal yang akan dipelajari merupakan benda mati, bukan makhluk hidup. Salah satu hal yang membedakan benda mati dengan makhluk hidup adalah persepsi. Makhluk hidup biasanya memberikan respons terhadap sesuatu (beban) menggunakan persepsi. Persepsi dapat berasal dari pengalaman maupun insting pribadi. Di sisi lain, benda tidak memiliki persepsi, respons benda terhadap beban cenderung dapat dipelajari dan dimengerti serta dihubungkan dengan persamaan-persamaan atau hukum-hukum yang selanjutnya ditetapkan manusia. Oleh karena itu, pemodelan terhadap sebuah sistem mekanika harus menggunakan akal tanpa persepsi. Dengan akal, maka respons sebuah sistem mekanika dapat dipahami dan dipelajari lebih dalam untuk menjawab problem yang ada.
Akal, dalam arti harfiah memiliki kata dasar berasal bahasa arab yang berarti tali. Hal ini dapat disimpulkan bahwa akal bukanlah pemikiran-pemikiran liar yang tidak jelas arahnya. Namun, akal adalah pemikiran-pemikiran yang terikat pada metode-metode tertentu yang jelas, batasan-batasan yang definitif, dan arah yang jelas. Metode, batasan, dan arah dalam proses pemodelan juga berperan penting dalam proses pemodelan. Dengan metode, batasan, dan arah yang jelas, pemodelan dapat disederhanakan sesederhana mungkin, karena semakin sederhana pemodelan, maka kesimpulan yang akan didapat akan semakin baik. Hal ini berkaitan dengan tujuan pemodelan digunakan adalah untuk mempelajari behavior tertentu dari sebuah sistem mekanika terkait dengan beban tertentu.
Pemodelan terhadap sebuah problem oleh Pak DAI dicontohkan menggunakan fondasi rumah panggung. Sebuah rumah panggung secara mekanik bisa jadi adalah sebuah sistem yang cukup kompleks. Untuk menyelesaikan masalah kekuatan fondasi, maka sistem tersebut dapat dilihat dari sisi mekanika statis. Kemudian fondasi rumah yang cukup rumit dapat disederhanakan cukup dengan gambar berikut.
Problem dan Proses Penyelesaian Masalah dalam ilmu mekanika
Problem dalam ilmu mekanika pasti selalu terkait dengan benda mati dan behavior nya. Behavior tersebut terkait dengan respons benda tersebut terhadap rangsangan atau beban. Dalam melakukan perancangan mesin, pengetahuan seorang insinyur mesin terkait behavior-behavior dari sistem-sistem mekanika yang digunakan sangat penting karena menjadi landasan dalam memperhitungkan kekuatan mesin, performa, serta kondisi lainnya. Seiring berjalannya waktu, proses perancangan menjadi semakin rumit dan semakin akurat, sehingga perlu dilakukan simulasi terhadap mesin yang dirancang untuk mengetahui kekuatan dan performanya.
Di sisi lain, dalam pengembangan ilmu teknik mesin, sebuah teori atau pendekatan baru perlu diuji terhadap hasil eksperimen. Terkadang, proses eksperimen yang dilakukan perlu menggunakan sumber daya yang banyak dan memakan waktu, sehingga sangat mahal. Pendekatan komputasi dapat dilakukan sebelum melakukan uji eksperimen agal peluang keberhasilan eksperimen menjadi lebih tinggi dan tidak menelan biaya yang terlalu banyak. Di sinilah manfaat komputasi teknik, selain untuk mengamalkan ilmu, juga dapat mengembangkan ilmu, khususnya bidang teknik mesin.
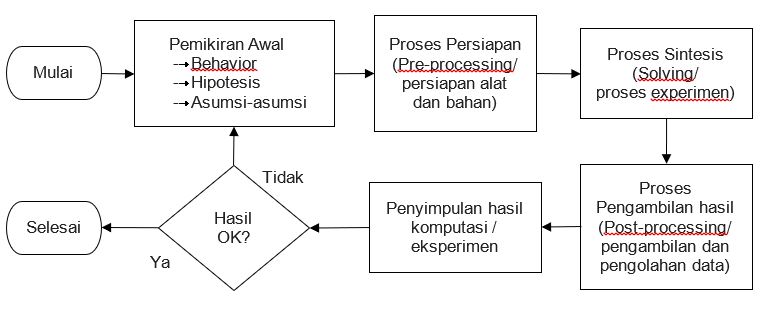
Dalam menyelesaikan masalah, seorang insinyur perlu menjalankan tahapan-tahapan tertentu yang baku agar hasil penyelesaian masalahnya baik dan dapat diterapkan. Tahapan-tahapan tertentu tersebut secara garis besar dapat digambarkan pada diagram berikut.
Dalam hal ini, peran penting seorang insinyur adalah pada pemberian pemikiran awal dan pembuat keputusan terkait sudah baik atau belumnya sebuah hasil pengujian. Apabila pengertian terkait behavior mesin, pemberian asumsi awal, dan pembuatan hipotesis dari insinyur terkait buruk, maka hasil pengujian juga akan buruk. Sebaliknya, seorang insinyur yang baik tentu dapat memberikan pemikiran awal yang baik dan memberikan keputusan yang baik.
Contoh kasus fondasi rumah menggunakan ees
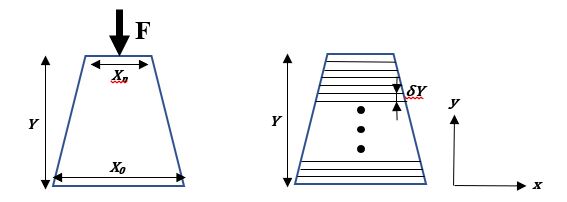
Fondasi rumah panggung yang dicontohkan oleh Pak DAI dapat dihitung distribusi tegangan dan regnggangannya secara komputasi dengan cara dibagi menjadi beberapa bagian (finite element). Berikut ilustrasi proses pembagiannya.
Dengan metode pembagian berdasarkan persamaan berikut.
Sehingga,
Kemudian didapat nilai Xi (lebar elemen tertentu) sebagai berikut.
Jika dari tampak atas bentuk fondasi adalah persegi, maka luas penampang elemen tertentu dan volumenya adalah,
Dan berat elemen tertentu dapat ditentukan dengan persamaan berikut.
Berdasarkan hukum Newton 3, akan terjadi saling memberikan aksi-reaksi pada permukaan antara masing-masing elemen, seperti yang tergambar pada persamaan berikut.
Dalam sebuah elemen yang diam, berlaku hukum Newton 2 sebagai berikut.
Tegangan normal yang dirasakan oleh masing-masing elemen adalah sebagai berikut.
Kemudian regangan yang terjadi pada masing-masing elemen adalah sebagai berikut
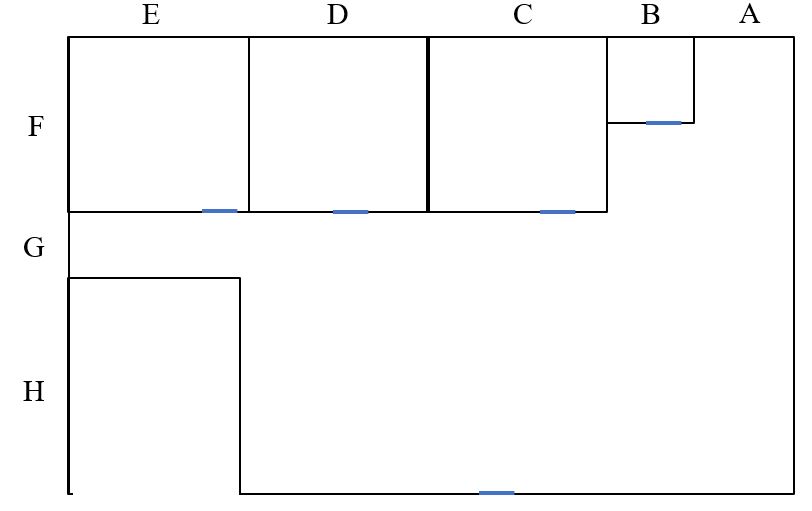
Berikut merupakan contoh hasil perhitungan dengan menggunakan EES dengan menggunakan jumlah elemen sebanyak 10 elemen dan diberi beban 20000N. Ditentukan tinggi fondasi adalah 0,5m, lebar bagian bawah 0,5m, lebar bagian atas adalah 0,3m, dan fondasi terbuat dari beton. Diketahui dari sumber[1][2], massa jenis beton adalah 2200kg/m3 dan modulus elastisitas beton adalah 2,35*10^10Pa.
Optimasi Biaya Pembangunan Rumah
Rumah merupakan salah satu kebutuhan pokok manusia yang harus dipenuhi di samping makanan dan pakaian. Dibandingkan dengan pakaian dan makanan, rumah merupakan kebutuhan pokok yang paling sulit dipenuhi karena memakan biaya yang sangat besar untuk memiliki sebuah rumah. Oleh karena itu, diperlukan strategi tertentu untuk menekan biaya pembangunan rumah agar seminimal mungkin. Dengan metode komputasi teknik, kita dapat melakukan optimasi pembangunan rumah dengan pemodelan matematis dan beberapa penyederhanaan. Dalam hal ini, optimasi yang dilakukan bersifat single objective, yaitu harga. Biaya yang diperhitungkan dalam pembangunan rumah dalam kasus ini hanya meliputi pembangunan lantai, atap, dan tembok. Unsur-unsur diluar itu (cat, sistem kelistrikan, perpipaan, lampu, dll) masih belum diperhitungkan dalam kasus ini.
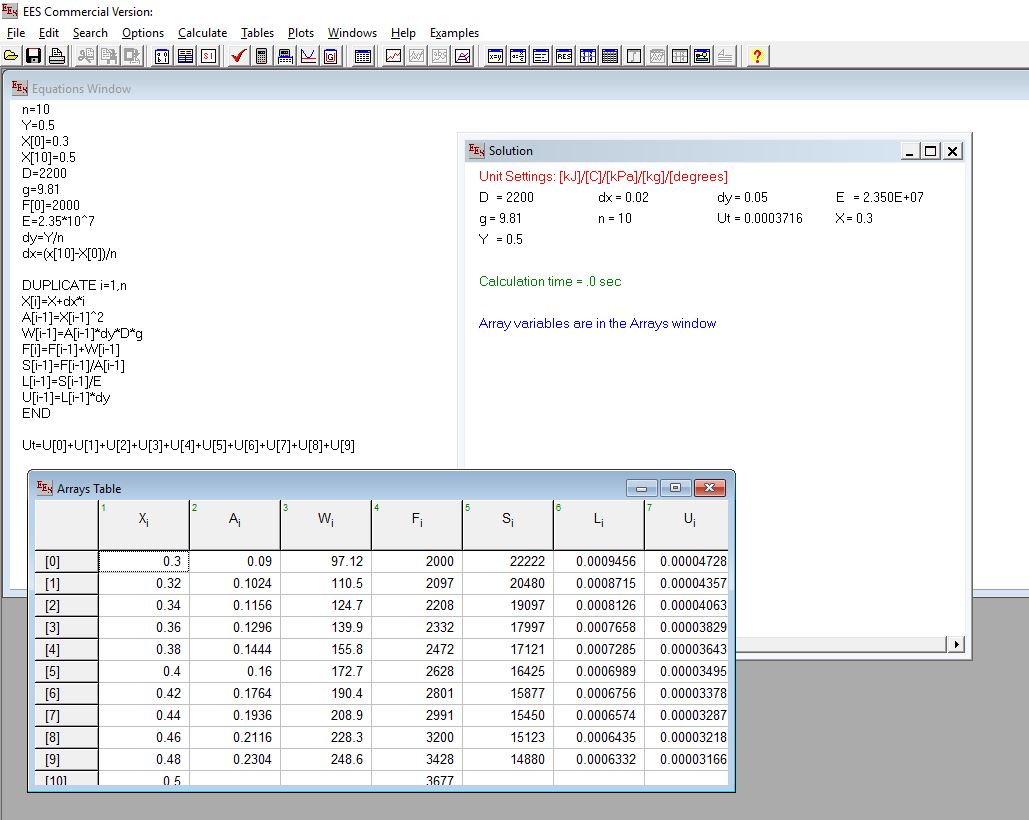
Sebagai langkah awal optimasi, ditetapkan beberapa spesifikasi awal dari rumah yang akan dibangun. Rumah yang akan dibangun merupakan rumah dengan tipe 36 sehingga luas bangunan yang tersedia adalah 72 m2 dengan ukuran panjang dan lebar dibebaskan. Rumah harus memiliki tiga kamar tidur, sebuah kamar mandi, sebuah dapur, serta sebuah car-port. Langkah selanjutnya, sketsa awal denah rumah yang akan dibuat adalah sebagai berikut. Tanda garis biru menandakan pintu.
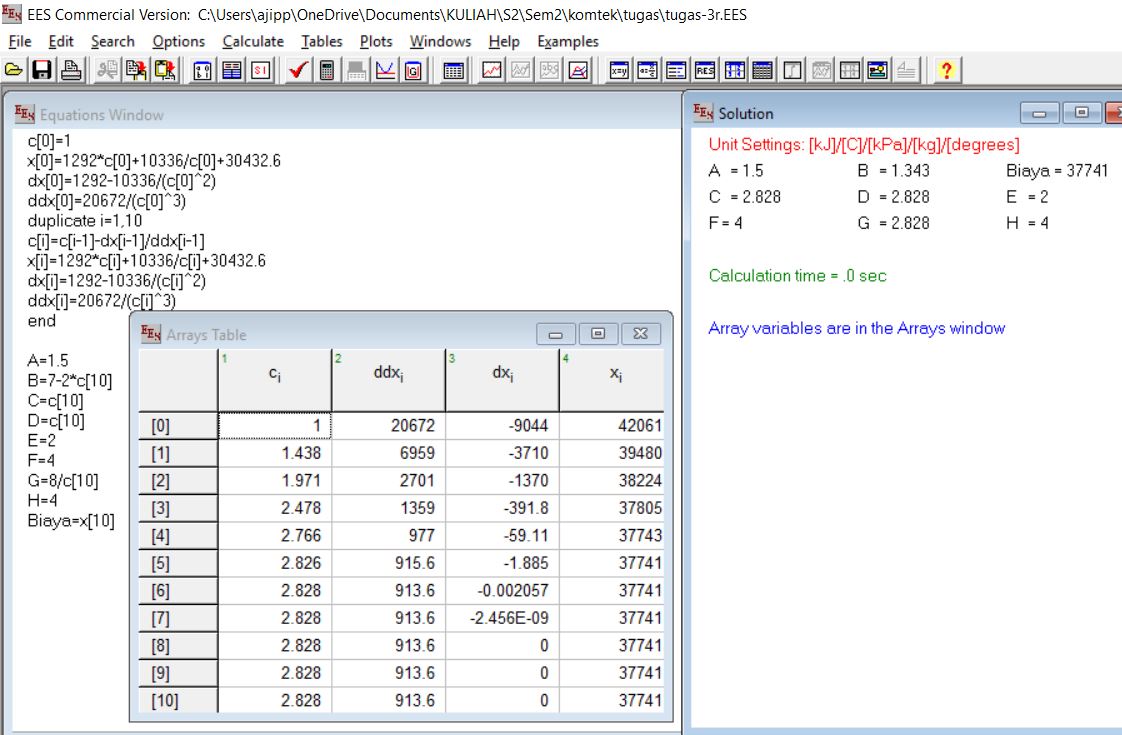
Luas bangunan yang dipatok 72 m2 menjadi constrain pertama dimana (A + B + C + D + E) X (F + G + H) = 72. Selanjutnya, berdasarkan pengalaman, sebuah car port paling tidak berukuran 3m x 4m. Sehingga menjadi constrain H = 4. Kemudian, ditetapkan pula paling tidak sebuah kamar memiliki luas 8 m2, dengan lebar tidak kuran dari 2 meter. Sehingga constrain selanjutnya adalah C x F = D x F = E x F = 8, selain itu, C = D = E, dengan 2 < C < 4, dan 2 < F < 4. Untuk kamar mandi ditetapkan berukuran 2x3m, sehingga B = 1.5. Untuk dapur yang berada di sebelah kamar mandi, paling tidak ada ruang untuk menaruh kompor sekitar 1 meter, sehingga 1 < A < 2.5. Agar seseorang dapat masuk kamar E,F, maka harus ada gap antara kamar E,F dengan car port, paling tidak 1m, sehingga ditetapkan G = 1 Setelah masing-masing constrain ditetapkan, dilakukan simulasi dasar apakah setiap constrain tidak saling bentrok, digunakan nilai minimum untuk A, B, C, D, dan E, yaitu, 1.5, 1, 2, 2, 2, sehingga lebar rumah minimal adalah 8,5 meter, padahal untuk car port dan kamar E,F saja paling tidak membutuhkan 8 meter, sehingga rancangan pertama sangat sulit untuk dilaksanakan. Langkah selanjutnya untuk memperbaiki rancangan adalah pengetatan constrain dan pembuatan sketsa baru.
Berikut adalah rancangan sketsa rumah setelah direvisi.