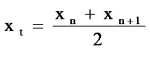Difference between revisions of "Metnum03 Bhismantyo Tsaqif Daniswara"
| Line 29: | Line 29: | ||
'''1.Hitung fungsi pada interval yang sama dari x sampai pada perubahan tanda dari fungsi f(xn) dan f(xn+1), yaitu :f(xn) . f(xn+1) < 0 | '''1.Hitung fungsi pada interval yang sama dari x sampai pada perubahan tanda dari fungsi f(xn) dan f(xn+1), yaitu :f(xn) . f(xn+1) < 0 | ||
'''2.Estimasi pertama dari akar xt dihitung dengan | '''2.Estimasi pertama dari akar xt dihitung dengan | ||
| − | ''' [[File:AkarbiseksiBhisma.png|150px|center]] | + | '''[[File:AkarbiseksiBhisma.png|150px|center]] |
'''3.Buat evaluasi berikut untuk menentukan di dalam sub interval mana akar persamaan berada : | '''3.Buat evaluasi berikut untuk menentukan di dalam sub interval mana akar persamaan berada : | ||
'''a.f(xn).f(xt) < 0, akar persamaan berada pada sub interval pertama, kemudian tetapkan xn+1 = xt dan lanjutkan pada langkah ke-4 | '''a.f(xn).f(xt) < 0, akar persamaan berada pada sub interval pertama, kemudian tetapkan xn+1 = xt dan lanjutkan pada langkah ke-4 | ||
'''b.f(xn).f(xt) > 0, akar persamaan berada pada sub interval kedua, kemudian tetapkan xn = xt dan lanjutkan pada langkah ke-4 | '''b.f(xn).f(xt) > 0, akar persamaan berada pada sub interval kedua, kemudian tetapkan xn = xt dan lanjutkan pada langkah ke-4 | ||
'''c.f(xn).f(xt) = 0, akar persamaan adalah xt dan hitungan selesai | '''c.f(xn).f(xt) = 0, akar persamaan adalah xt dan hitungan selesai | ||
| + | '''4.Hitung perkiraan baru dari akar dengan | ||
| + | '''[[File:AkarbiseksiBhisma.png|150px|center]] | ||
Revision as of 19:21, 17 November 2020
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُ
Biodata Diri
Nama : Bhismantyo Tsaqif Daniswara
NPM : 1806181754
Program Studi : S1 Pararel Teknik Mesin
Contents
[hide]Pertemuan 01
Pada pertemuan pertama ini, Pak Dai menjelaskan dan mengarahkan mengenai pelajaran Metode Numerik sebelum UTS. Pada page ini, saya akan menjelaskan apa yang sudah saya pelajari mengenai Metode Numerik.
Metode untuk mencari akar-akar persamaan
1. Metode Tertutup
a. Metode Biseksi
Metode Biseksi memiliki beberapa langkah-langkah penyelesaian sebagai berikut :
1.Hitung fungsi pada interval yang sama dari x sampai pada perubahan tanda dari fungsi f(xn) dan f(xn+1), yaitu :f(xn) . f(xn+1) < 0 2.Estimasi pertama dari akar xt dihitung dengan
3.Buat evaluasi berikut untuk menentukan di dalam sub interval mana akar persamaan berada : a.f(xn).f(xt) < 0, akar persamaan berada pada sub interval pertama, kemudian tetapkan xn+1 = xt dan lanjutkan pada langkah ke-4 b.f(xn).f(xt) > 0, akar persamaan berada pada sub interval kedua, kemudian tetapkan xn = xt dan lanjutkan pada langkah ke-4 c.f(xn).f(xt) = 0, akar persamaan adalah xt dan hitungan selesai 4.Hitung perkiraan baru dari akar dengan