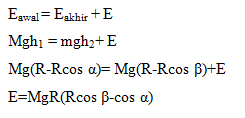Difference between revisions of "Isyroqialghifari"
| (6 intermediate revisions by the same user not shown) | |||
| Line 395: | Line 395: | ||
Selamat malam, semoga kita semua selalu diberi kesehatan dalam kondisi seperti ini. Kalian semua sahabat saya yang luar biasa, dari satu persamaan bisa dibahas secara menyeluruh dan mendalam. Dari rumus A1.v1=A2.v2 , dP = f L rho V^2 / 2 D , serta yang lebih kompleks seperti saudara adhika yaitu Turbulent Viscosity . du/dy . sqrt(L. pi . 4) / sqrt(Luas Area Pipa) = dp. Maka dari itu saya menjelaskan dimana kembali jika A adalah luasan dimana akan berpengaruh kepada kecepatan dan lainnya. Dari rumus yang dijelaskan oleh saudara Dieter dan saudari Desy serta dari sahabat- saya yang lainnya yg saya tidak bisa sebut satu per satu karena jumlahnya cukup banyak. Maka dari rumus A1.v1=A2.v2 dan dP = f L rho V^2 / 2 D yang sudah dijelaskan sebelum2nya, maka luasan sangat berpengaruh terhadap kecepatan serta pressure drop yang dihitung. Semakin besar luasan maka pressure drop akan semakin mengecil. Karena luasan berbanding terbalik dengan pressure drop. | Selamat malam, semoga kita semua selalu diberi kesehatan dalam kondisi seperti ini. Kalian semua sahabat saya yang luar biasa, dari satu persamaan bisa dibahas secara menyeluruh dan mendalam. Dari rumus A1.v1=A2.v2 , dP = f L rho V^2 / 2 D , serta yang lebih kompleks seperti saudara adhika yaitu Turbulent Viscosity . du/dy . sqrt(L. pi . 4) / sqrt(Luas Area Pipa) = dp. Maka dari itu saya menjelaskan dimana kembali jika A adalah luasan dimana akan berpengaruh kepada kecepatan dan lainnya. Dari rumus yang dijelaskan oleh saudara Dieter dan saudari Desy serta dari sahabat- saya yang lainnya yg saya tidak bisa sebut satu per satu karena jumlahnya cukup banyak. Maka dari rumus A1.v1=A2.v2 dan dP = f L rho V^2 / 2 D yang sudah dijelaskan sebelum2nya, maka luasan sangat berpengaruh terhadap kecepatan serta pressure drop yang dihitung. Semakin besar luasan maka pressure drop akan semakin mengecil. Karena luasan berbanding terbalik dengan pressure drop. | ||
Sekian dari saya, semoga semua mendapat bonus nilai dan tidak ada yang dikurangi. AAMIIN | Sekian dari saya, semoga semua mendapat bonus nilai dan tidak ada yang dikurangi. AAMIIN | ||
| + | |||
| + | Sistem pada gedung bertingkat | ||
| + | |||
| + | [[File:lapafitro1.jpg|800px]] | ||
| + | [[File:lapafitro2.jpg|800px]] | ||
| + | [[File:lapafitro3.jpg|800px]] | ||
| + | [[File:lapafitro4.jpg|800px]] | ||
| + | [[File:lapafitro5.jpg|800px]] | ||
| + | [[File:lapafitro6.jpg|800px]] | ||
| + | [[File:lapafitro7.jpg|800px]] | ||
| + | [[File:lapafitro8.jpg|800px]] | ||
| + | [[File:lapafitro9.jpg|800px]] | ||
| + | [[File:lapafitro10.jpg|800px]] | ||
| + | [[File:lapafitro11.jpg|800px]] | ||
| + | [[File:lapafitro12.jpg|800px]] | ||
| + | [[File:lapafitro13.jpg|800px]] | ||
| + | [[File:lapafitro14.jpg|800px]] | ||
| + | [[File:lapafitro15.jpg|800px]] | ||
| + | [[File:lapafitro16.jpg|800px]] | ||
| + | [[File:lapafitro17.jpg|800px]] | ||
| + | [[File:lapafitro18.jpg|800px]] | ||
| + | [[File:lapafitro19a.jpg|800px]] | ||
| + | [[File:lapafitro20.jpg|800px]] | ||
| + | [[File:lapafitro21.jpg|800px]] | ||
| + | [[File:lapafitr022.jpg|800px]] | ||
| + | [[File:lapafitro23.jpg|800px]] | ||
| + | [[File:lapafitro24.jpg|800px]] | ||
| + | [[File:lapafitro25.jpg|800px]] | ||
| + | [[File:lapafitro26.jpg|800px]] | ||
| + | [[File:lapafitro27.jpg|800px]] | ||
| + | [[File:lapafitro28.jpg|800px]] | ||
| + | [[File:lapafitro29.jpg|800px]] | ||
| + | [[File:lapafitro30.jpg|800px]] | ||
| + | [[File:lapafitro31.jpg|800px]] | ||
| + | [[File:lapafitro32.jpg|800px]] | ||
| + | [[File:lapafitro33.jpg|800px]] | ||
| + | [[File:lapafitro34.jpg|800px]] | ||
| + | [[File:lapafitro35.jpg|800px]] | ||
| + | [[File:lapafitro36.jpg|800px]] | ||
| + | [[File:lapafitro37.jpg|800px]] | ||
| + | [[File:lapafitro38.jpg|800px]] | ||
| + | [[File:lapafitro39.jpg|800px]] | ||
| + | [[File:lapafitro40.jpg|800px]] | ||
| + | |||
| + | [[File:lapafitro1b.jpg|800px]] | ||
| + | [[File:lapafitro2b.jpg|800px]] | ||
| + | [[File:lapafitro3b.jpg|800px]] | ||
| + | |||
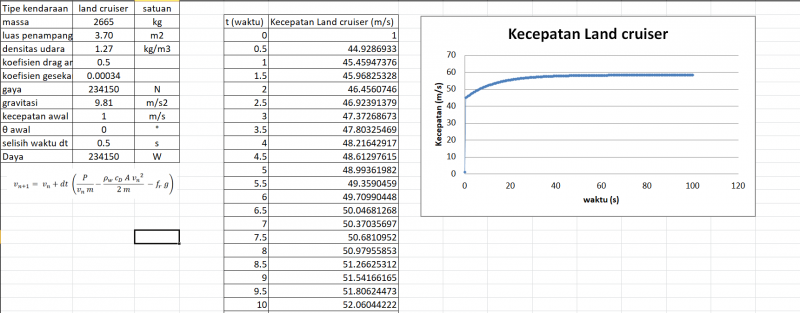
| + | == UAS Komputasi Teknik == | ||
| + | |||
| + | [[File:UAS GHI1.jpeg|800px]] | ||
| + | [[File:UAS GHI2.jpeg|800px]] | ||
| + | [[File:UAS GHI3.png|800px]] | ||
Latest revision as of 20:26, 10 June 2020
Contents
- 1 Data diri
- 2 Komputasi Teknik
- 3 sinopsis skripsi
- 4 korelasi skripsi pada komputasi Teknik
- 5 istilah dalam komputasi Teknik
- 6 Project permodelan tugas akhir
- 7 Pertemuan Ke Empat 24 Februari 2020
- 8 Optimasi Kebutuhan Energi Manusia
- 9 Pertemuan ke enam 9 maret 2020
- 10 UTS Komputasi Teknik
- 11 Pertemuan ke sekian
- 12 Pertemuan ke sekian
- 13 Quiz komputasi teknik
- 14 Pertemuan ke sekian
- 15 Pertemuan ke sekian
- 16 Pertemuan ke sekian
- 17 UAS Komputasi Teknik
Data diri
Nama : Isyroqi Al Ghifari
NPM : 1906324082
Jurusan : Teknik Mesin - Teknik kendaraan dan peralatan berat
Komputasi Teknik
Menurut saya komputasi teknik adalah suatu algoritma untuk memecahkan suatu masalah dari data yang di input. Pada dasarnya semua output atau hasil dari pemograman tergantung dari input dan proses pada saat pemrosesan dalam komputasi. Serta pada penggunaannya dapat membantu kebutuhan manusia yang notabene pekerjaan tersebut terbatas dilakukan oleh manusia.
Beberapa pemograman yang saya pernah tau tentang komputasi teknik yaitu pada penggunaan ansys cfx dan fluent untuk mengetahui laju aliran dari fluida. Serta beberapa software seperti nastran patran untuk mengetahui nilai kekuatan dari suatu model.
Tetapi pada umumnya saya lebih sering menggunakan komputasi Teknik dengan Ms.excel dalan menyelesaikan perhitungan data data yang didapat dari sebuah sumber
sinopsis skripsi
skripsi saya dengan judul Analisa Kekuatan Impak, Tarik, dan Mikrografi Aluminium 5083 Akibat Pengelasan MIG (Metal Inert Gas) dengan Variasi Posisi Pengelasan. Alasan saya memilih judul skripsi seperti diatas karena masih jarangnya penelitian tentang variasi posisi pengelasan dan pengaplikasian aluminium 5083 dengan pengelasan MIG (metal inert gas). Oleh karena itu saya memilih judul seperti diatas. Dan pengaplikasian aluminium 5083 dalam pembuatan kapal sekarang sudah mulai banyak karena material aluminium yang minim korosif dibandingkan dengan baja. Serta pengelasan dengan MIG (Metal Inert Gas) merupakan salah satu pengelasan yang sudah mulai digunakan oleh banyak produksi kapal khususnya kapal aluminium.
Dalam skripsi saya ini, dapat diketahui bahwa posisi las memiliki peranan penting dalam metode pengelasan. Oleh karenanya sangat diperhatikan apabila pengelasan dengan posisi apa yang akan dilakukan. Posisi pengelasan dapat dilakukan dengan 4 posisi yaitu dengan down hand, horizontal, vertical, dan over head. Maka dapat diketahui posisi down hand adalah posisi terbaik yang dilakukan welder dalam pengelasan. Karena posisi down hand adalah posisi yang paling mudah serta paling efisien dan paling baik hasilnya dibandingkan dengan posisi pengelasan yang lainnya.
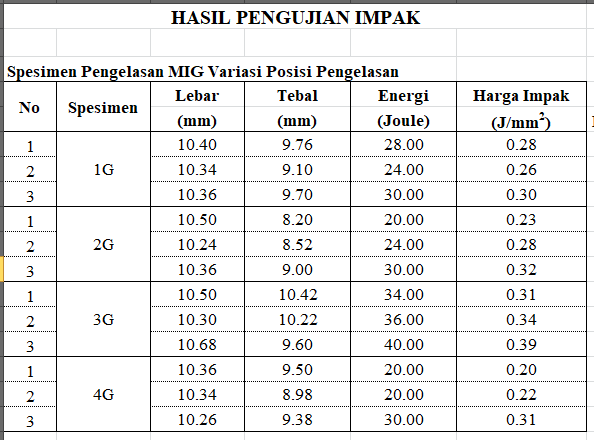
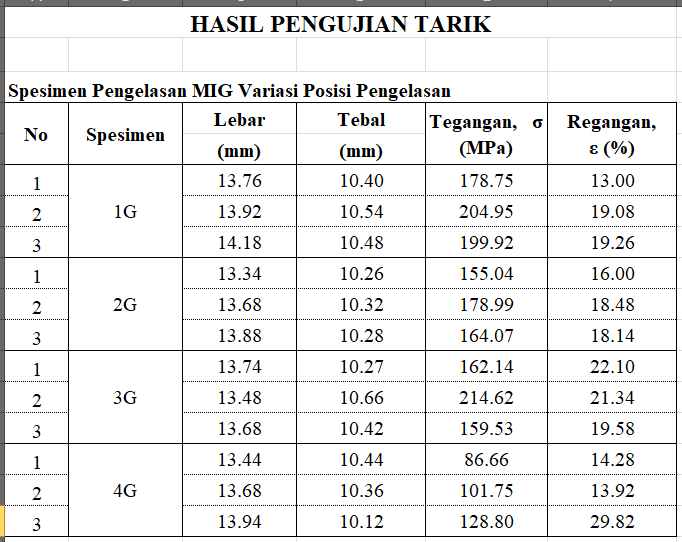
Aluminium 5083 pada kapal umumnya digunakan sebagai bahan baku pembuatan kapal aluminium khususnya pada bagian lambung. Pengelasan MIG(Metal Inert Gas) merupakan salah satu jenis pengelasan yang dapat diterapkan dalam pengelasan aluminium. Penelitian ini bertujuan untuk mengetahui hasil dari uji impak tarik , dan struktur mikrografi dari sambungan las jenis single v butt joint 60° dengan perbedaan posisi pengelasan pada Aluminium 5083. Dari penelitian ini dapat diketahui bahwa posisi pengelasan cukup berpengaruh terhadap hasil kekuatan dari sambungan las. Hasil penelitian menunjukkan bahwa kekuatan tegangan tarik rata-rata terbesar didapat pada pengelasan dengan posisi 1G sebesar 194,54 MPa, sedangkan regangan rata-rata terbesar didapat pada pengelasan dengan posisi 3G sebesar 21,01 %, Sedangkan modulus elastisitas rata-rata terbesar didapat pada pengelasan posisi 1G sebesar 11,62 GPa, dan hasil harga impak rata-rata terbesar didapat pada pengelasan dengan posisi 3G sebesar 0,35 J/mm2. Pada struktur mikro posisi pengelasan 1G memiliki hasil struktur mikro yang lebih rapat pada daerah HAZ(Heat Affected Zone) dan daerah pengelasan dibanding dengan posisi pengelasan 2G, 3G, dan 4G
korelasi skripsi pada komputasi Teknik
korelasi yang berhubungan dengan komputasi Teknik adalah dalam perhitungan hasil pengujian impak dan Tarik pada spesimen yang telah dilakukan pengujian. Komputasi Teknik juga berperan penting dalam penelitian saya karena hasil hitungan didapatkan dengan komputasi Teknik. Dalam pengerjaannya saya menggunakan Ms. Excel sebagai salah satu software komputasi yang saya gunakan. Karena setelah melakukan eksperimen pengujian, hanya mendapatkan angka mentah dalam berbentuk Joule pada pengujian impak dan Pmaks pada pengujian Tarik. Padahal perhitungan belum selesai sampai disitu dan masih berlanjut. Untuk pengujian impak hasil akhirnya menggunakan satuan harga impak yaitu joule/mm2 dan pengujian Tarik hasil akhirnya menggunakan satuan MPa.
istilah dalam komputasi Teknik
Istilah komputasi tentunya sudah tidak asing lagi. Begitu banyak dan beragam istilah-istilah yang kita dapat ketahui pada komputasi Teknik. Contohnya yaitu pada istilah yang saya jelaskan dibawah
1. Topik: stokastik (Isyroqi Al Ghifari) a. Definisi Yang dimaksud dengan stokastik menurut Oxford Dictionary (1993) menakrifkan proses stokastik sebagai suatu barisan kejadian yang memenuhi hukum-hukum peluang. Hull (1989, hlm.62) menyatakan bahwa setiap nilai yang berubah terhadap waktu dengan cara yang tidak tertentu (dalam ketidakpastian) dikatakan mengikuti proses stokastik.
b. Kapan dilakukan? Proses stokastik digunakan untuk memodelkan evolusi suatu sistem yang mengandung suatu ketidakpastian atau sistem yang dijalankan pada suatu lingkungan yang tidak dapat diduga, dan pada saat bersamaan model deterministik tidak lagi cocok dipakai untuk menganalisis sistem
c. Bagaimana melaksanakan stokastik? Proses stokastik dapat dikelompokkan berdasarkan jenis jenis ruang pada parameternya, ruang keadaannya, dan kaitan antara pengubah acak yang membentuk proses stokastik tersebut
d. Mengapa perlu stokastik? Proses stokastik diperlukan pada saat model deterministik tidak lagi cocok digunakan untuk menganalisis system
Project permodelan tugas akhir
Project tugas akhir penulis melakukan eksperimen pengujian impak dan tarik aluminium 5083 dengan pengelasan MIG variasi posisi pengelasan
Pertama tama yaitu melakukan pengelasan dengan MIG Pada saat pengelasan MIG dapat diketahui heat input yaitu
HI=(60 x E x I)/v
Dimana: HI = Heat Input (Joule/cm) I = Kuat Arus (Ampere) E = Tegangan Busur (volt) v = Kecepatan Las (cm/menit)
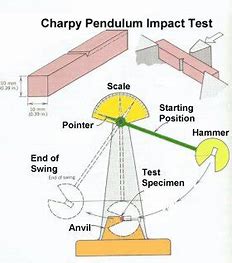
Pada pengujian impak diketahui sebagai berikut
Pergerakan pada pendulum impak dapat dketahui sebagai berikut
m = massa
g = gravitasi
r = jari jari pendulum
cos a = sudut awal pendulum
cos b = sudut akhir pendulum
Pada pengujian tarik diketahui berikut :
Stress (Tegangan Mekanis):
σ = F/A
Dimana:
F = gaya tarikan
A = luas penampang
Strain (Regangan):
ε = ΔL/L
Dimana:
ΔL = Pertambahan panjang
L = Panjang awal
Maka, hubungan antara stress dan strain dirumuskan:
E = σ/ε
Dimana:
E = Modulus Elastisitas
σ = Stress (Tegangan)
ε = Strain (Regangan)
Pertemuan Ke Empat 24 Februari 2020
SOAL QUIZ PERTEMUAN KE EMPAT
1. Tuliskan persamaan-persamaan matematik yang Anda pahami dalam kuliah Matematika Teknik Lanjut semester lalu !
2. Jelaskan makna fisik (teknik) dari persamaan No 1 !
3. Jelaskan cara penyelesaian pada persamaan No. 1 !
4. Terapkan (aplikasikan) pengetahuan/keterampilan analisis matematis Anda untuk menyusun model matematis project/kasus Komputasi Teknik !
5. Jelaskan metode yang akan Anda pakai untuk studi No. 4
Pengertian FEM, FVM, dan FDM
FEM adalah singkatan dari Finite Element Method, dalam bahasa Indonesia disebut Metode Elemen Hingga. Konsep paling dasar FEM adalah, menyelesaikan suatu problem dengan cara membagi obyek analisa menjadi bagian-bagian kecil yang terhingga. Bagian-bagian kecil ini kemudian dianalisa dan hasilnya digabungkan kembali untuk mendapatkan penyelesaian untuk keseluruhan daerah. Kata “finite atau terhingga” digunakan untuk menekankan bahwa bagian-bagian kecil tersebut tidak tak terhingga, seperti yang lazim digunakan pada metode integral analitik
FVM adalah singkatan dari Finite Volume Method yang artinya pendekatan yang umum digunakan dalam kode CFD. Persamaan yang mengatur diselesaikan melalui volume kontrol diskrit. Metode volume terbatas menyusun kembali persamaan diferensial parsial yang mengatur (biasanya persamaan Navier-Stokes) dalam bentuk konservatif, dan kemudian discretize persamaan baru. Hal ini menjamin konservasi fluks melalui volume kontrol tertentu. Yang terbatas menghasilkan persamaan volume yang mengatur persamaan.
FDM adalah singkatan dari Finite Difference Method atau Metode Beda Hingga, memiliki sejarah penting dan sederhana untuk program. Hal ini saat ini hanya digunakan dalam kode khusus beberapa. Modern Kode beda hingga menggunakan sebuah batas tertanam untuk menangani geometri yang kompleks, membuat kode-kode yang sangat efisien dan akurat. Cara lain untuk menangani geometri termasuk penggunaan tumpang tindih grid, dimana solusinya adalah interpolated di jaringan masing-masing
SKRIPSI
Judul : Analisa Kekuatan Impak, Tarik, dan Mikrografi Aluminium 5083 Akibat Pengelasan MIG (Metal Inert Gas) dengan Variasi Posisi Pengelasan
Aluminium 5083 pada kapal umumnya digunakan sebagai bahan baku pembuatan kapal aluminium khususnya pada bagian lambung. Pengelasan MIG(Metal Inert Gas) merupakan salah satu jenis pengelasan yang dapat diterapkan dalam pengelasan aluminium. Penelitian ini bertujuan untuk mengetahui hasil dari uji impak tarik , dan struktur mikrografi dari sambungan las jenis single v butt joint 60° dengan perbedaan posisi pengelasan pada Aluminium 5083. Dari penelitian ini dapat diketahui bahwa posisi pengelasan cukup berpengaruh terhadap hasil kekuatan dari sambungan las. Hasil penelitian menunjukkan bahwa kekuatan tegangan tarik rata-rata terbesar didapat pada pengelasan dengan posisi 1G sebesar 194,54 MPa, sedangkan regangan rata-rata terbesar didapat pada pengelasan dengan posisi 3G sebesar 21,01 %, Sedangkan modulus elastisitas rata-rata terbesar didapat pada pengelasan posisi 1G sebesar 11,62 GPa, dan hasil harga impak rata-rata terbesar didapat pada pengelasan dengan posisi 3G sebesar 0,35 J/mm2. Pada struktur mikro posisi pengelasan 1G memiliki hasil struktur mikro yang lebih rapat pada daerah HAZ(Heat Affected Zone) dan daerah pengelasan dibanding dengan posisi pengelasan 2G, 3G, dan 4G
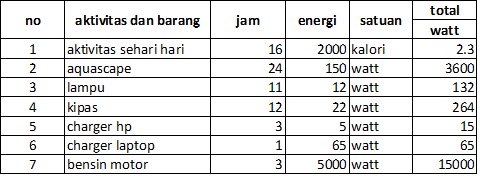
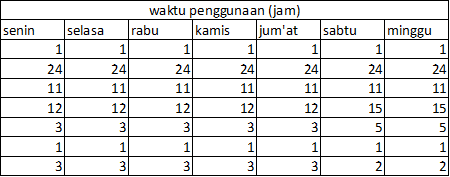
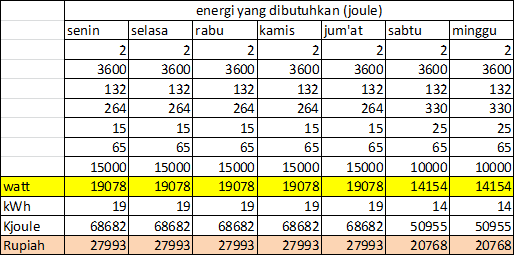
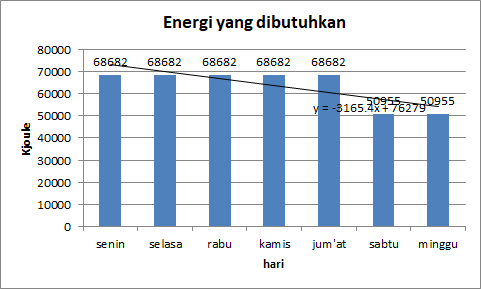
Optimasi Kebutuhan Energi Manusia
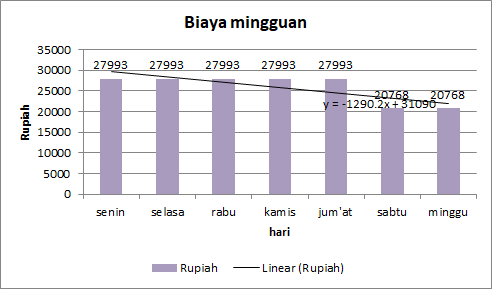
Pada pertemuan kemarin, membahas tentang kebutuhan kalori serta keinginan dalam kehidupan sehari hari. Untuk mengetahui berapa kebutuhan kalori dalam tubuh bisa menggunakan rumus basal metabolic rate (BMR). BMR adalah jumlah energi yang dikeluarkan tubuh selama satu hari dalam kondisi istirahat atau tidak beraktivitas berat. Rumus BMR menggunakan persamaan Harris Benedict, yang direvisi oleh Roza dan Shizgal pada tahun 1984, sebagai berikut:
- BMR Pria = 88.362 + (13.397 x berat badan [kg]) + (4.799 x tinggi badan [cm]) – (5.677 x umur)
- BMR Wanita = 447.593 + (9.247 x berat badan [kg]) + (3.098 x tinggi badan [cm]) – (4.33 x umur)
dibawah adalah beberapa hasil perhitungan kalori kebutuhan dalam sehari
Pertemuan ke enam 9 maret 2020
Rule of thumb komputasi Teknik
1. Initial Thinking (Menganalisis masalah, pada tahapan ini pengumpulan data dan survei dapat dilakukan untuk mengetahui kedepannya)
2. Develop Model Matematis
3. Simulasi (Menjalankan sebuah "angka" berdasarkan rumusan / eksekusi terhadap model)
4. Verifikasi (Solve the equation right. Menguji apakah tidak ada kesalahan numerik, ini termasuk bentuk dan jumlah mesh....)
5. Validasi (Solve the right equation. Menguji kebenaran dari model, dalam tahapan ini bisa di rasakan yang paling pertama adalah dengan perasaan oleh engineer apakah hasil dari validasi tepat atau tidak. Setelahnya dapat dilakukan perbandingan atau merujuk dari penelitian sebelumnya)
UTS Komputasi Teknik
UTS KOMPUTASI TEKNIK 2020.
1. Silahkan setiap mhs membuat video presentasi hasil belajar setiap minggu (baik pengetahuan (konsep/teori) dan keterampilan (menggunakan komputasi teknik).
2. Membuat laporan hasil tugas optimasi kebutuhan energi manusia.
3. Menyiapkan draft paper project komputasi teknik.
Jawaban
1. Untuk nomor ini saya menggunakan ANSYS sebagai media pembelajaran saya dalam komputasi Teknik. Karena saya baru masuk dalam dunia perangkat lunak dalam komputasi Teknik.
Berikut adalah video saya tentang pembelajaran tentang komputasi Teknik
2.Optimasi kebutuhan energi manusia.
Pada kali ini saya mencantumkan beberapa kebutuhan energi saya pada setiap harinya
3. Draft paper project komputasi Teknik
Pertemuan ke sekian
Pada ksesmpatan ini saya akan menampilkan video hasil pembelajaran serta pembelajaran yang sedikit berhubugan dengan project komputasi teknik. Yang nantinya akan berkesinambungan dengan mempelajari sedikit demi sedikit serta adanya penambahan beberapa keterampilan yang nantinya menghasilkan ilmu yang InsyaAllah bermanfaat untuk orang lain. Pada kesempatan ini video akan sedikit membahas tentang spesimen uji tarik yang nantinya akan diketahui stress serta strain dari spesimen tersebut
Pertemuan ke sekian
video draft project komputasi teknik
Quiz komputasi teknik
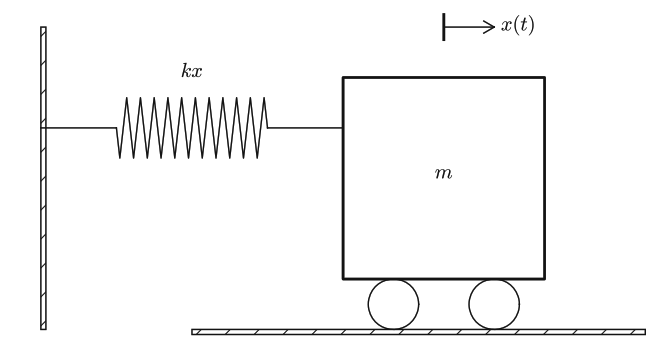
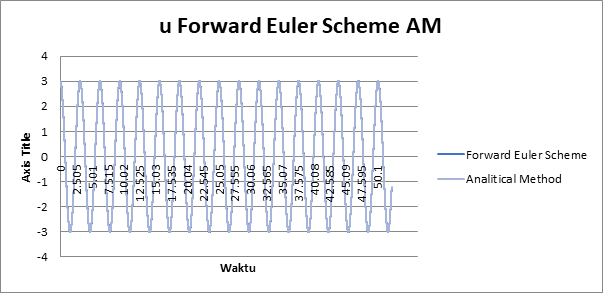
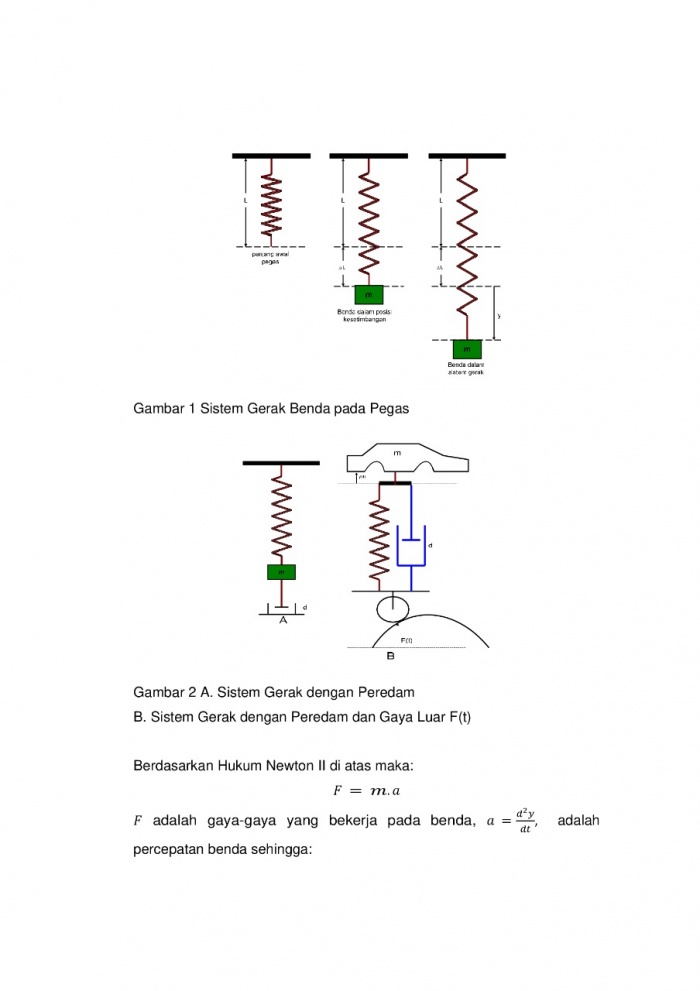
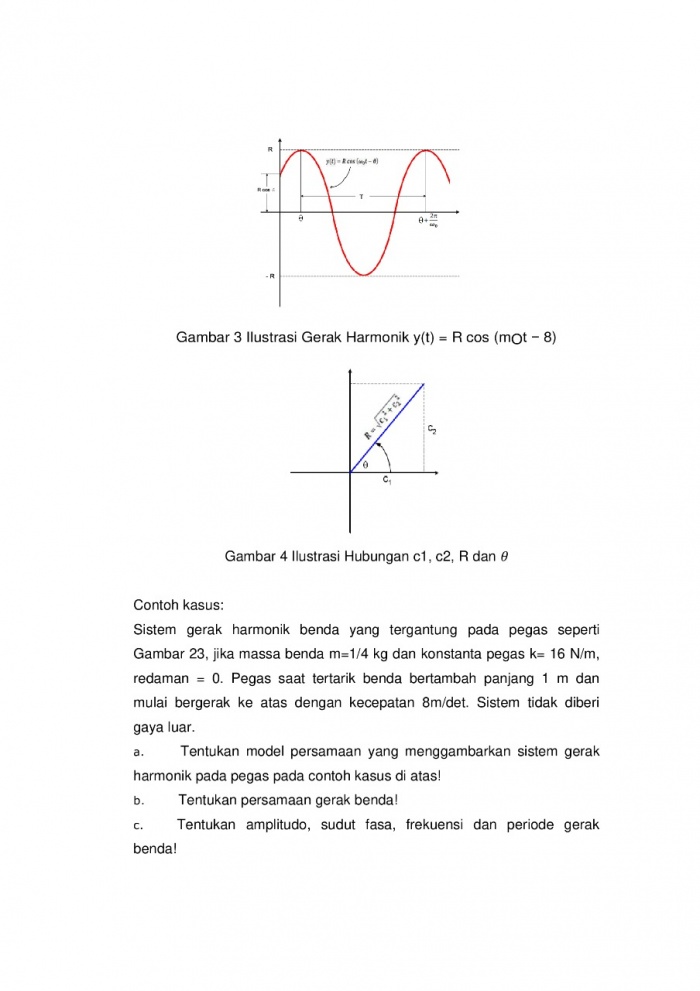
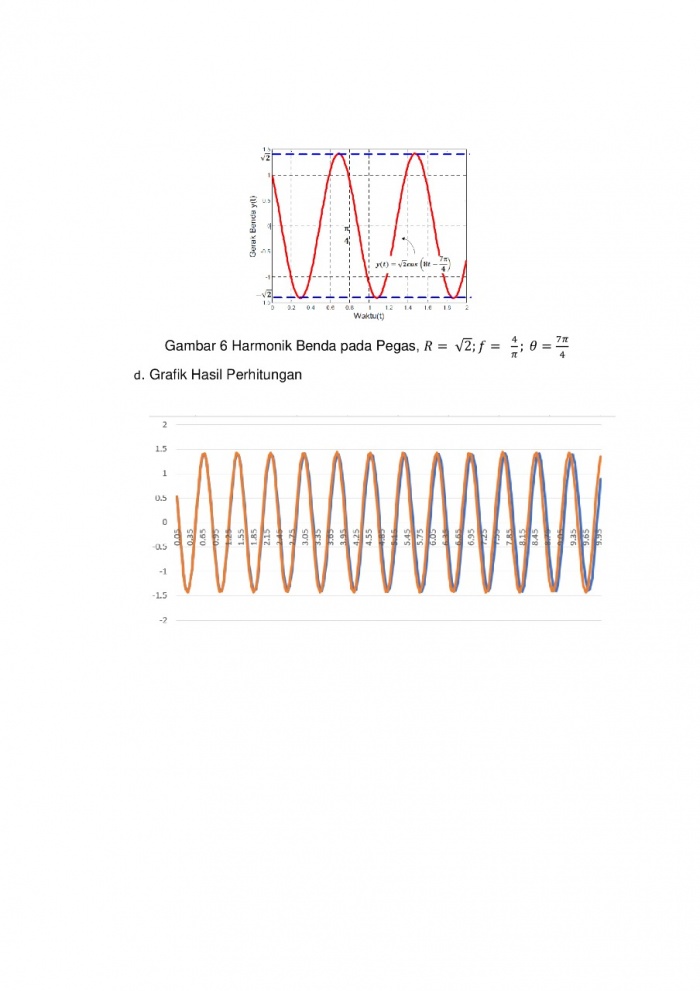
Oscillating One-dimensional Systems
• Pemikiran Awal Kasus yang dipelajari kali ini mengenai pergerakan bolak-balik benda satu dimensi. Suatu massa (m) yang dihubungkan dengan suatu pegas ditarik pada jarak tertentu (x) dan dilepaskan (kecepatan v awal = 0). Model ini menganggap tidak ada gesekan pada massa maupun pegas.
• Pemodelan Matematis Pada pemodelan matematis sesuai gambar diatas kita dapat menghitung gaya F = ma, dan F = -kx -kx = ma a + ω2x = 0 Jika perpindahan dari model diatas dibuat dalam bentuk lingkaran, maka kita dapat merepresentasikan perpindahan dengan u = u0 cos ωt dan v = v0 ω sin ωt • Perhitungan Numerik u’ = v v’ = -ω2u menghasilkan skema komputasi un+1 = un + ∆t vn vn+1 = vn - ∆t ω2un Pada skema Forward Euler kita dapat mengganti un pada persamaan kecepatan menjadi un+1 sesuai yang sudah dihitung pada time step sebelumnya sehingga persamaan menjadi un+1 = un + ∆t vn vn+1 = vn - ∆t ω2un+1
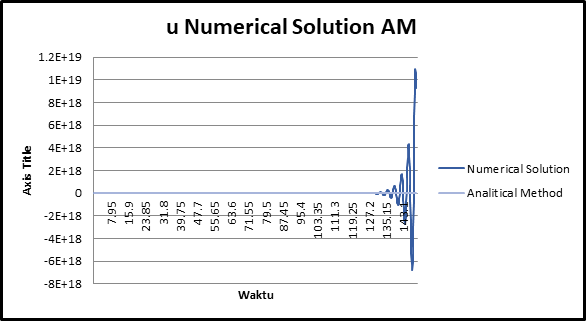
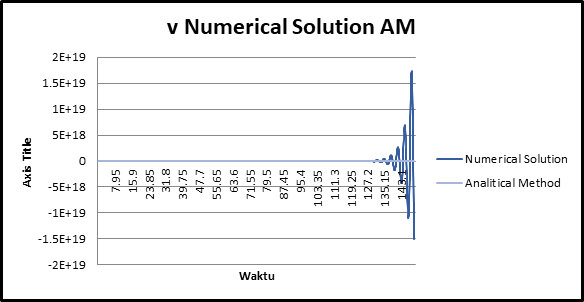
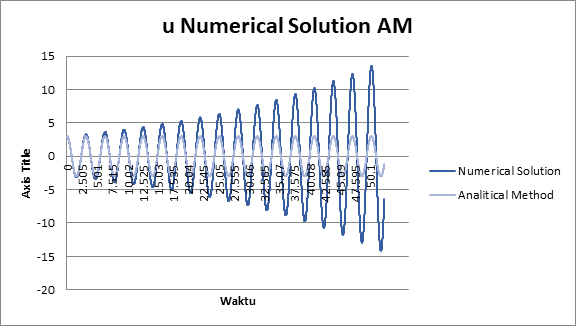
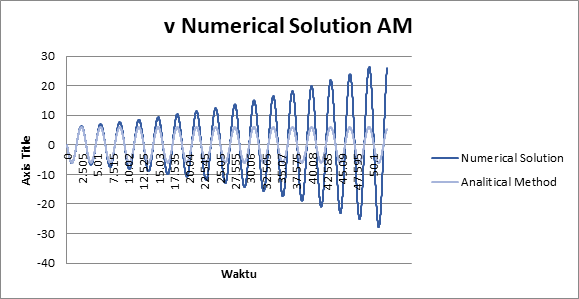
• Verifikasi Perbandingan Numerical Solution tanpa skema Forward Euler dengan Perhitungan Analisis
Time steps 0,15
Time steps 0,015
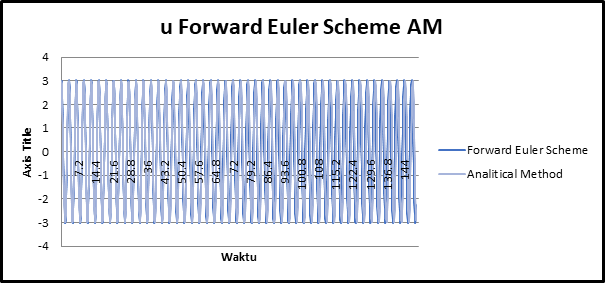
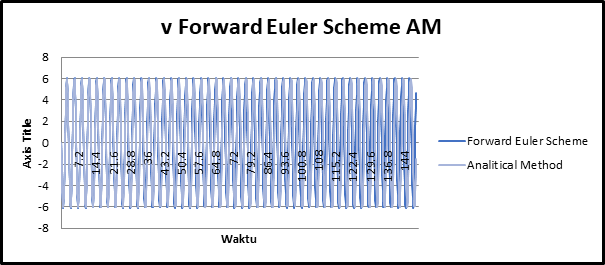
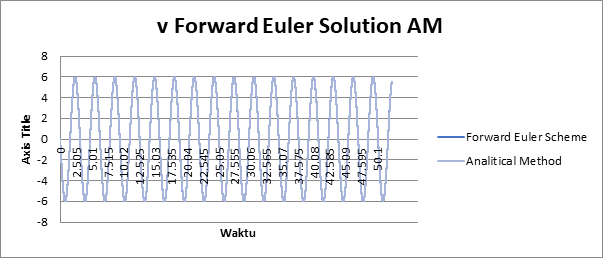
Perbandingan Numerical Solution memakai skema Forward Euler dengan Perhitungan Analisis
Time steps 0,15
Time Steps 0,015
Pembahasan Hasil Perhitungan Perhitungan Numerik yang dilakukan tanpa skema Forward Euler memiliki tingkat error yang semakin lama semakin tinggi, sedangkan perhitungan numerik dengan skema Forward Euler memiliki tingkat error yang lebih kecil dan stabil dibandingkan dengan perhitungan analitis. Parameter lain yang berpengaruh adalah time step atau biasa disebut time resolution, pada pemodelan excel kali ini digunakan time step 0,15 detik dan 0,015 detik. Time step yang lebih kecil (0,015 detik) menandakan resolusi sampel yang lebih baik sehingga tingkat error yang semakin kecil, sedangkan time step yang besar (0,15 detik) menandakan resolusi sampel kurang baik sehingga tingkat error kurang dibandingkan time step yang lebih kecil. Maka dari itu, penggunaan data time step yang lebih kecil dapat dijadikan pertimbangan dalam perhitungan karena menghasilkan error yang lebih kecil bila dibandingkan dengan data time step yang lebih besar. Serta penggunaan jumlah data dapat disesuaikan dalam perhitungan agar menghasilkan grafik yang nantinya dapat lebih enak untuk dipandang serta menjadikan nilai sampel yang lebih besar.
Pertemuan ke sekian
Pertemuan ke sekian
translate paper Simplified Finite Elements model to represent Mass-Spring structures in dynamic simulation karya Rúbia M. Bosse, André Teófilo Beck
Abstrak
Makalah ini menyajikan pendekatan langkah demi langkah, didaktik untuk membangun model elemen hingga yang disederhanakan (Finite Element/FE)mereproduksi hasil yang diperoleh dengan model mass-spring (MS) atau bangunan geser. Tujuan utamanya adalah untuk mengekspos keterbatasan masing-masing model, dan untuk memfasilitasi perbandingan antara hasil numerik yang diperoleh dengan model yang berbeda,sangat sering oleh penulis yang berbeda. Contoh aplikasi adalah sistem kontrol getaran, analisis model teoritis, mesin pemodelan komponen dan jaringan lunak. Makalah ini menyajikan hipotesis yang diperlukan untuk membangun hierarkis model, membahas pengaruh masing-masing asumsi / penyederhanaan dalam respons struktural. Dengan tujuan ini, komputer kode diimplementasikan untuk menyelesaikan struktur kerangka 2D di bawah beban dinamis dengan model pegas massal dan posisi model elemen hingga mempertimbangkan analisis geometrik nonlinier. Hasil penelitian menunjukkan bahwa hipotesis yang diajukan adalah cukup untuk mereproduksi dalam metode FE respon yang sama dari model MS mengalami impuls dan beban gempa.
1. PENDAHULUAN
Dua metodologi utama yang digunakan untuk mengevaluasi perilaku mekanik struktur seperti bangunan di bawah beban dinamis adalah model Mass-Spring (MS) dan model Finite Element (FE). Penerapan masing-masing teknik ini biasanya tergantung pada jenis struktur, keakuratan analisis yang diminta, dan kompleksitas struktur. Telah diketahui bahwa semua model menghadirkan ketidakpastian terkait kesetiaan untuk mewakili perilaku struktural yang nyata. Dalam hal ini, interpretasi kritis terhadap penyederhanaan dan keterbatasan model teknik diperlukan untuk analisis dan desain yang andal.
Secara umum, model massa-pegas memiliki pendekatan diskrit dan formulasi matematika sederhana. Massa terkonsentrasi dalam titik-massa dan terhubung satu sama lain dengan pegas linier yang mewakili kekuatan elastis internal yang bekerja di antara massa. Model MS sederhana karena menghasilkan sangat sedikit derajat kebebasan, di mana persamaan gerak dapat diselesaikan secara analitis dengan modal superposisi. Ini secara signifikan mengurangi waktu pemrosesan untuk analisis dinamis. Model massa-pegas populer karena secara konsep lebih sederhana dan lebih mudah diimplementasikan daripada model yang lebih konsisten secara fisik berdasarkan metode elemen hingga. Selain itu, model MS sangat fleksibel untuk perubahan topologi.
Formulasi ini biasanya diterapkan untuk mewakili struktur sebagai sistem kontrol getaran, bangunan dalam perilaku global, elemen mesin dan bahan jaringan lunak. Model MS juga sangat berlaku untuk melakukan analisis keandalan dan respon stokastik, di mana biaya komputasi merupakan masalah mendasar, karena struktur perlu dipecahkan secara berulang. Kelemahan utama dari model MS adalah bahwa mereka dianggap tidak tepat untuk memperkirakan perilaku mekanik struktur yang dapat dideformasi. Model MS mengabaikan persamaan konstitutif material, dan menghadirkan sejumlah derajat kebebasan yang mungkin terlalu kecil untuk jenis analisis tertentu.
Beberapa kemajuan telah dibuat dalam model MS untuk meningkatkan representasi realistis dari struktur yang dapat dideformasi. Beberapa penelitian mengusulkan metode baru untuk mendapatkan koefisien kekakuan pegas, yang lain telah menyarankan modifikasi model tradisional (Kuether dan Allen, 2012, Geethu et al., 2015), termasuk misalnya pegas nonlinear dan piezometrik dalam analisis sistem kontrol getaran (Harne, 2013), penggabungan pegas kontak kubik untuk mensimulasikan kehilangan kontak (Huajiang dan Guan, 2016) dan pemecah implisit cepat untuk model MS standar (Liu et al., 2013, Zheng et al., 2017)
Di sisi lain, metode elemen hingga (FE) berasal dari mekanika kontinum dan menjadi salah satu metode yang paling sering digunakan untuk memecahkan masalah sistem mekanik. Metode FE memerlukan penggunaan komputer secara intensif dan biaya komputasinya dapat menjadi penghalang untuk analisis skala besar. Namun, teknik ini mampu mensimulasikan sistem fisik yang kompleks, menyelesaikan masalah multi-dimensi dengan nonlinier (Dhatt, Touzot dan Legrançois, 2012).
Model FE mendiskritisasi struktur dalam elemen-elemen kecil untuk merepresentasikan perilaku berkelanjutan. Metode ini menggunakan pendekatan variabel yang tidak diketahui untuk mengubah persamaan diferensial parsial menjadi persamaan aljabar yang diselesaikan melalui metode numerik. Model FE cocok untuk mengevaluasi respons berbagai struktur, terutama karena undang-undang dasar material dipertimbangkan dalam formulasi matematika. Namun, kemajuan ini ada harganya: semakin halus modelnya, semakin kompleks solusinya, yang mengarah ke biaya komputasi yang besar.
Tantangan yang cukup besar di bidang metode FE adalah pertimbangan perpindahan besar dalam tubuh yang cacat. Upaya penelitian membahas pengembangan formulasi yang mempertimbangkan efek nonlinier dalam bahan konstitutif atau dalam kondisi batas (perpindahan atau rotasi besar). Dalam masalah perpindahan besar, deskripsi Total Lagrangian menunjukkan metode yang efisien untuk menyelesaikan masalah dinamis struktur padat, karena mempertimbangkan konfigurasi referensi yang unik dan tetap: matriks massa tetap konstan dan solusi keseimbangan dinamis diperoleh dengan lebih mudah. Solusi masalah yang mempertimbangkan analisis geometri nonlinear dengan deskripsi Total Lagrangian dapat diverifikasi dalam Mondkar dan Powell (1977), Wood dan Zienkiewicz (1977), Surana (1983), Coda dan Greco (2004). Pendekatan alternatif untuk merepresentasikan analisis nonlinier geometris menggunakan deskripsi Lagrangian total adalah model FE posisional. Dalam teknik ini, parameter nodal adalah koordinat nodal (posisi) dan dimungkinkan untuk menggunakan kinematika Reissner yang tepat dalam evaluasi perpindahan dan rotasi untuk struktur rangka. Contoh aplikasi dari formulasi ini dapat dilihat di Coda dan Paccola (2014), Reis dan Coda (2014), dan Siqueira dan Coda (2016, 2017).
Saat ini, dengan kemajuan teknik komputasi untuk meningkatkan waktu pemrosesan, model FE yang disempurnakan semakin dapat diterapkan untuk menyelesaikan masalah mekanis apa pun. Dalam makalah ini, kami bermaksud untuk mendefinisikan hipotesis yang berlaku untuk model FE untuk membuatnya mewakili hasil yang kompatibel dengan model massa-pegas dengan idealisasi kerangka geser. Ini juga merupakan tujuan untuk mengamati dan mengukur perbedaan yang disebabkan oleh hipotesis ini dalam respon struktur, mengevaluasi keuntungan dan keterbatasan masing-masing model untuk memperkirakan respon struktur yang terkena berbagai sumber beban dinamis.
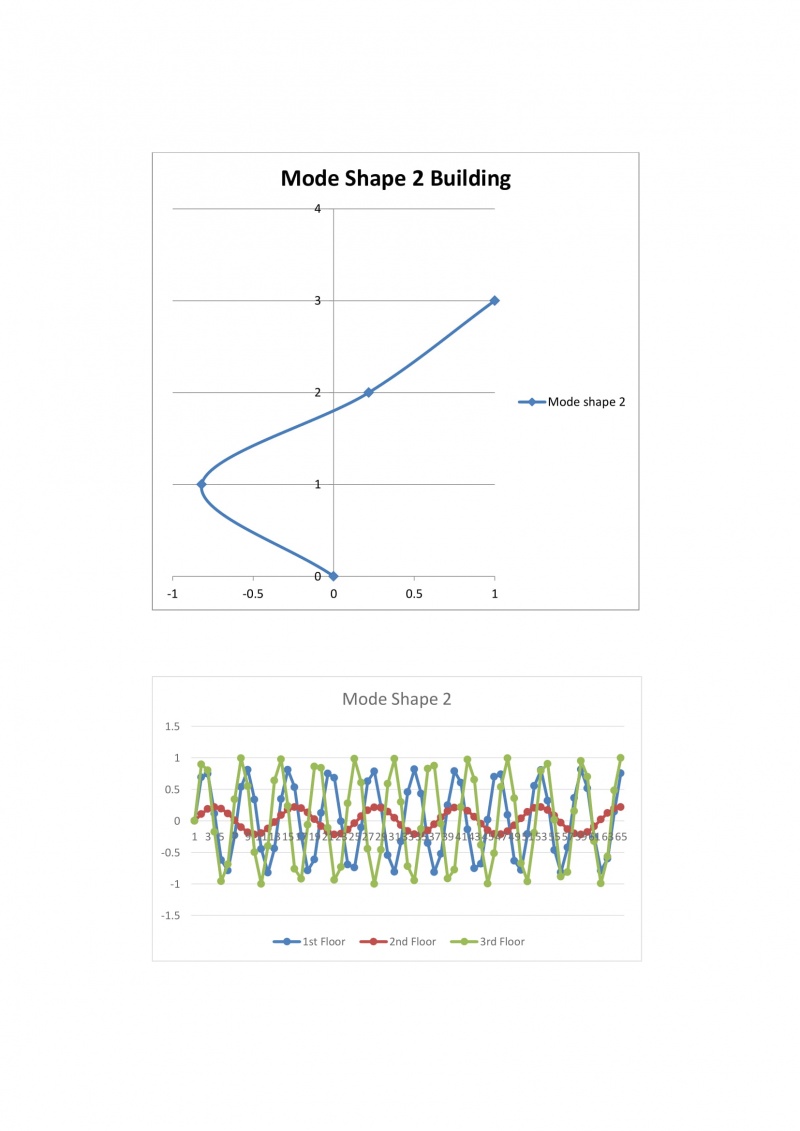
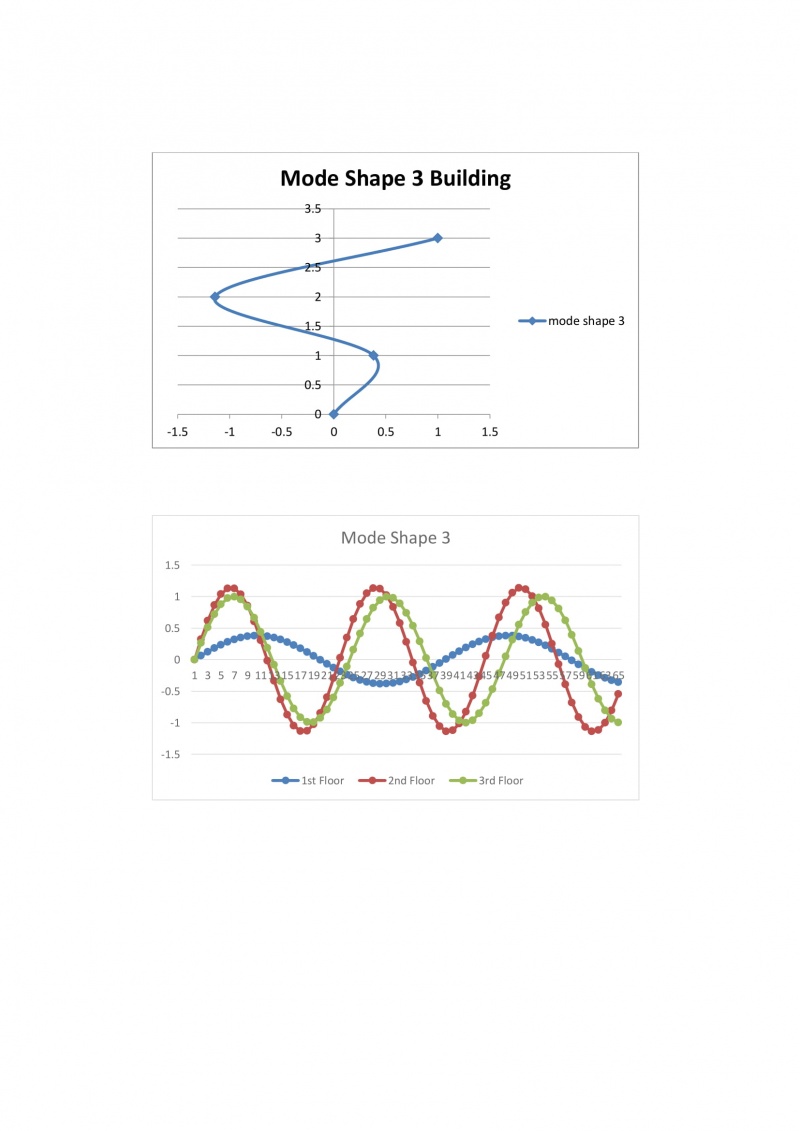
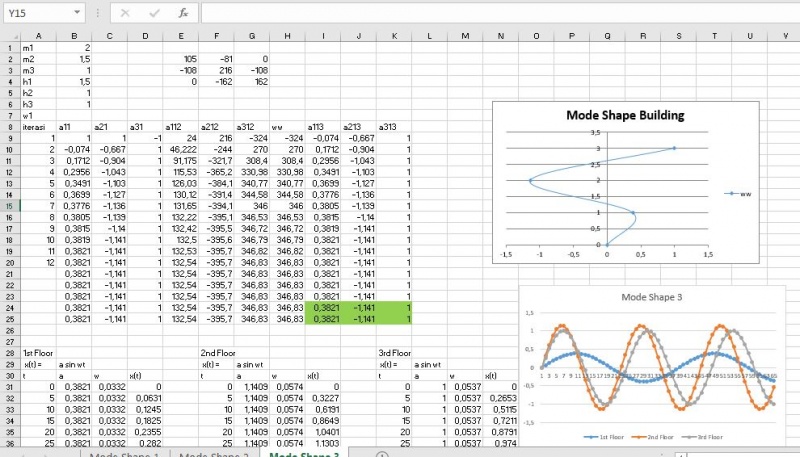
Untuk melakukan analisis ini, kode komputasi diterapkan untuk kedua model: model FE posisional dan model MS. Contoh-contoh yang disajikan dalam makalah ini berkaitan dengan struktur rangka yang tidak terbungkus yang dapat mewakili bangunan. Contoh 1 dan 2 memperlihatkan struktur satu dan lima lantai yang tereksitasi oleh gaya impuls. Contoh ketiga berkaitan dengan struktur yang sama dari contoh 2 yang bersemangat dengan catatan Gempa Bumi El Centro. Respons dalam domain waktu dan frekuensi dipelajari.
Pertemuan ke sekian
Isyroqi Al Ghifari - 1906324082 Selamat malam, semoga kita semua selalu diberi kesehatan dalam kondisi seperti ini. Kalian semua sahabat saya yang luar biasa, dari satu persamaan bisa dibahas secara menyeluruh dan mendalam. Dari rumus A1.v1=A2.v2 , dP = f L rho V^2 / 2 D , serta yang lebih kompleks seperti saudara adhika yaitu Turbulent Viscosity . du/dy . sqrt(L. pi . 4) / sqrt(Luas Area Pipa) = dp. Maka dari itu saya menjelaskan dimana kembali jika A adalah luasan dimana akan berpengaruh kepada kecepatan dan lainnya. Dari rumus yang dijelaskan oleh saudara Dieter dan saudari Desy serta dari sahabat- saya yang lainnya yg saya tidak bisa sebut satu per satu karena jumlahnya cukup banyak. Maka dari rumus A1.v1=A2.v2 dan dP = f L rho V^2 / 2 D yang sudah dijelaskan sebelum2nya, maka luasan sangat berpengaruh terhadap kecepatan serta pressure drop yang dihitung. Semakin besar luasan maka pressure drop akan semakin mengecil. Karena luasan berbanding terbalik dengan pressure drop. Sekian dari saya, semoga semua mendapat bonus nilai dan tidak ada yang dikurangi. AAMIIN
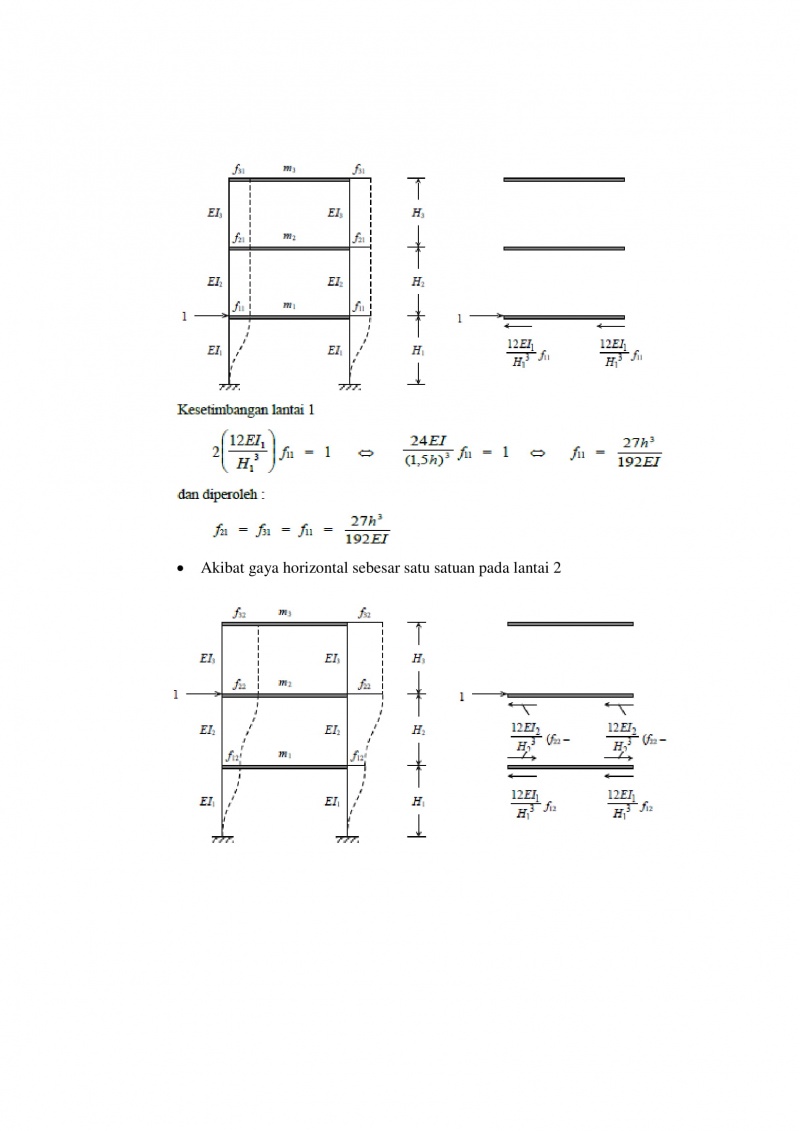
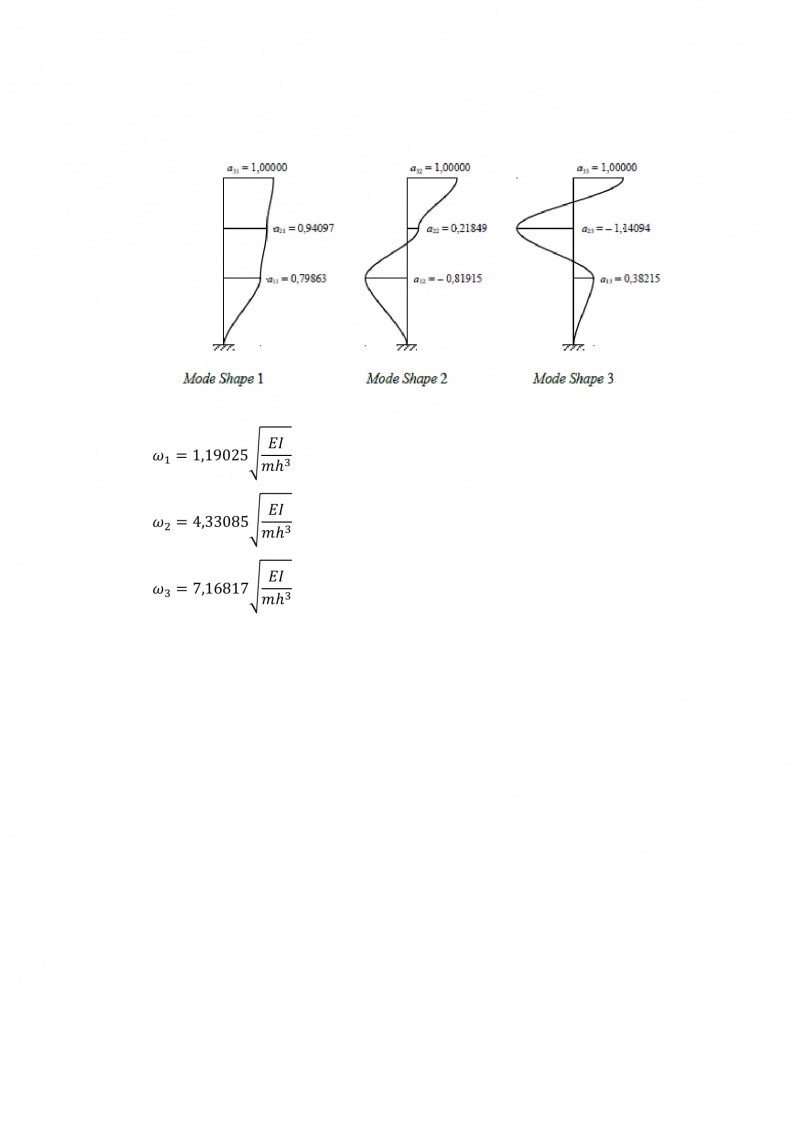
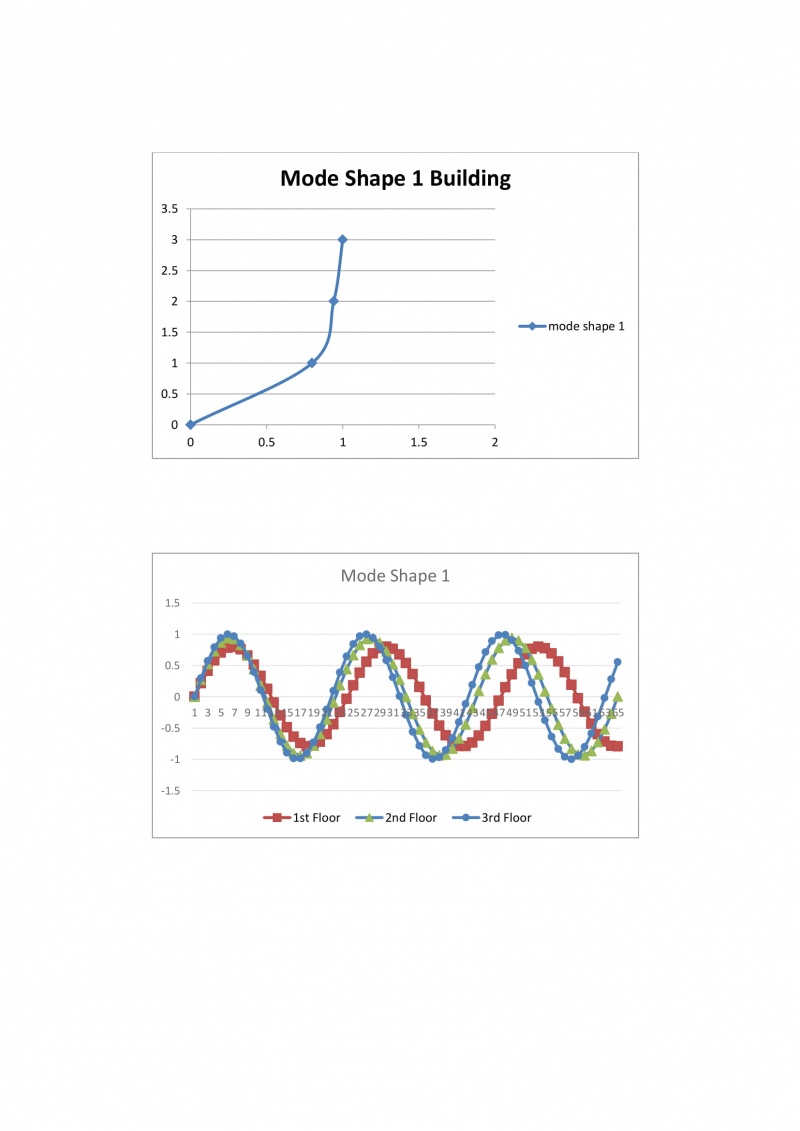
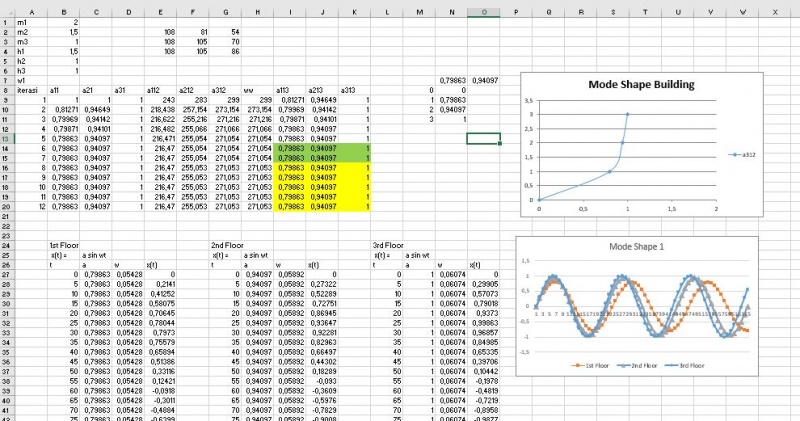
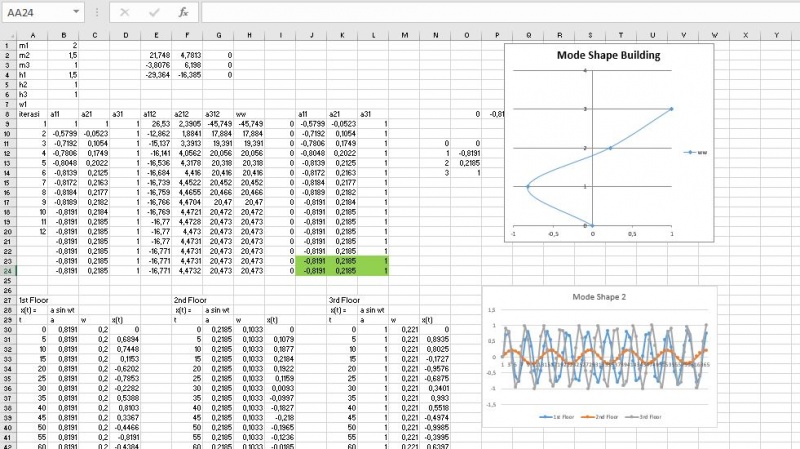
Sistem pada gedung bertingkat