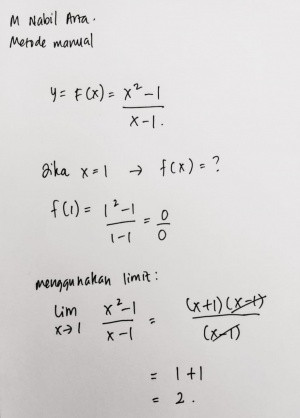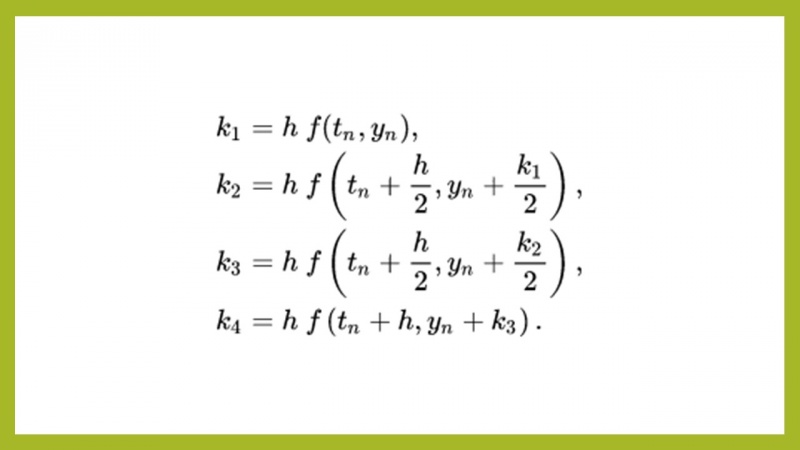Difference between revisions of "User:Mnabilarta"
Mnabilarta (talk | contribs) |
Mnabilarta (talk | contribs) |
||
| (16 intermediate revisions by the same user not shown) | |||
| Line 16: | Line 16: | ||
Email : thenabilarta@gmail.com | Email : thenabilarta@gmail.com | ||
| − | |||
| − | |||
| − | |||
| Line 28: | Line 25: | ||
Pertemuan pertama kelas metode numerik ini diisi oleh perkenalan dosen yang akan mengajar kelas metode numerik yaitu Dr. Ir. Ahmad Indra Siswantara dan Prof.Dr. Ir. Harinaldi, M.Eng. dilanjutkan oleh langsung membuat halaman pada wiki. | Pertemuan pertama kelas metode numerik ini diisi oleh perkenalan dosen yang akan mengajar kelas metode numerik yaitu Dr. Ir. Ahmad Indra Siswantara dan Prof.Dr. Ir. Harinaldi, M.Eng. dilanjutkan oleh langsung membuat halaman pada wiki. | ||
| − | Tugas 1 | + | Tugas 1 : Menentukan nilai f(x)= x^2-1/x-1 dengan x=1 |
| Line 36: | Line 33: | ||
| − | + | Menggunakan Phyton Spyder 3.7 | |
| Line 73: | Line 70: | ||
| − | + | Menggunakan kalkulator matrix didapatkan | |
| Line 84: | Line 81: | ||
| − | + | Perhitungan matrix menggunakan Phyton Spyder | |
| Line 95: | Line 92: | ||
Menyelesaikan soal yang berkaitan dengan GLBB gerak jatuh bebas di Phyton. | Menyelesaikan soal yang berkaitan dengan GLBB gerak jatuh bebas di Phyton. | ||
| + | |||
| + | |||
| + | [[File:Soalnbl2.jpeg|500px]] | ||
| + | |||
| + | |||
| + | Dengan menggunakan Phyton Spyder | ||
| + | |||
| + | |||
| + | [[File:Jawabannbltugas2.jpg|800px]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Tugas pertemuan kedua (3) : Power Point | ||
| + | |||
| + | Progres belajar metode numerik. | ||
| + | |||
| + | |||
| + | [[File:Lappembelajarannbl1.JPG|800px]] | ||
| + | |||
| + | |||
| + | [[File:Lappembelajarannbl2.JPG|800px]] | ||
| + | |||
| + | |||
| + | [[File:Lappembelajarannbl3.JPG|800px]] | ||
| + | |||
| + | |||
| + | ==Pertemuan Ketiga== | ||
| + | Semua rumus hanya berupa pendekatan karena tidak ada rumus atau simulasi yang akan sama dengan kejadian aslinya. | ||
| + | Permodelan diantaranya yaitu : prinsip konservasi massa, hukum newton (F = m.a), hukum konservasi energi. | ||
| + | |||
| + | Mencari modul matematis dari pegas yaitu gerakan bolak-balik. | ||
| + | |||
| + | Tugas Asistensi : PPT Laporan Asistensi | ||
| + | |||
| + | |||
| + | [[File:Pptassist1nbl1.JPG|800px]] | ||
| + | |||
| + | |||
| + | [[File:Pptassist1nbl2.JPG|800px]] | ||
| + | |||
| + | |||
| + | [[File:Pptassist1nbl3.JPG|800px]] | ||
| + | |||
| + | |||
| + | |||
| + | Tugas Aplikasi Runge-Kutta pada soal | ||
| + | |||
| + | |||
| + | [[File:Rungekuttanblsoal.jpg]] | ||
| + | |||
| + | |||
| + | [[File:Rungekuttanbljawab1.jpg|800px]] | ||
| + | |||
| + | |||
| + | ==Pertemuan Keempat== | ||
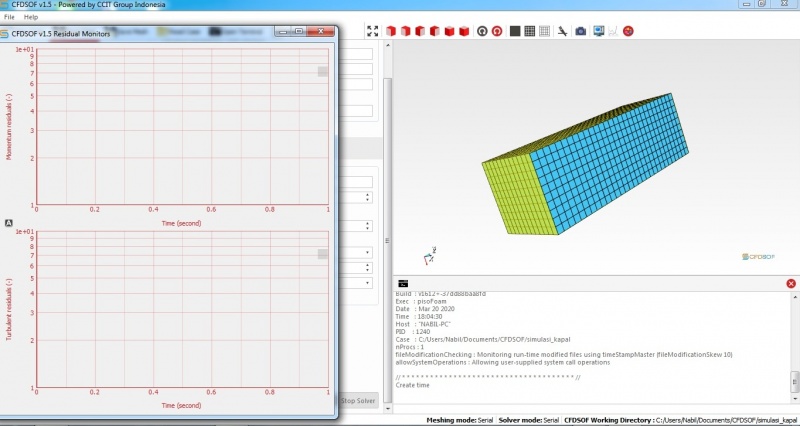
| + | Pada pertemuan keempat, Pak Da'i menjelaskan tentang rumus-rumus. Rumus-rumus hanya merupakan pendekatan jadi tidak bisa dianggap bahwa rumus akan sepenuhnya menyamai kondisi keadaan sesungguhnya. Selanjutnya diisi dengan asistensi dengan sebuah program CFD yaitu program yang mensimulasikan sebuah kapal selam yang berada di dalam laut. Program tersebut menghitung hubungan fluida dengan kapal selam tersebut dengan variabel seperti hambatan, turbulensi, dan semacamnya. | ||
| + | |||
| + | |||
| + | [[File:Imagenbl1.jpg|800px]] | ||
| + | |||
| + | |||
| + | [[File:Imagenbl2.jpg|800px]] | ||
| + | |||
| + | |||
| + | Saya sudah mengikuti contoh yang disediakan di tutorial dan mengambil salah satu contoh file obj kapal selam dari internet. Saya sudah melakukan langkah yang sama seperti yang dilakukan pada tutorial akan tetapi saya belum dapat menghasilkan penyelesaian yang sama. | ||
| + | |||
| + | Pada sesi Asistensi, kami ditugaskan untuk mengubah grafik yang didapat menjadi lebih dapat dihitung dengan menggunakan regresi. Regresi itu sendiri dilakukan pada pemrograman Phyton. | ||
| + | |||
| + | Tugas pertemuan keempat : resume | ||
| + | |||
| + | |||
| + | [[File:Pptassist2nbl1.JPG|800px]] | ||
| + | |||
| + | |||
| + | [[File:Pptassist2nbl2.JPG|800px]] | ||
| + | |||
| + | |||
| + | [[File:Pptassist2nbl3.JPG|800px]] | ||
| + | |||
| + | |||
| + | ==Pertemuan kelima== | ||
| + | Nilai merupakan ukuran performa dari seorang murid. | ||
| + | Tujuan dasar metode numerik adalah kemampuan menyelesaikan konsep dalam perhitungan sederhana. Pada zaman sekarang sudah ada tiga cara memecahkan sebuah kasus yaitu dengan teori, numerik, dan eksperimen. | ||
| + | |||
| + | Perbedaan antara Boundary dan Initial Value Problem. Pada Boundary Value Problem kita tidak mengetahui apa yang terjadi di dalam proses tapi kita tahu batas-batasannya yang dievaluasi setiap waktu. | ||
| + | |||
| + | Initial Value problem kita tahu sesaat sebelum proses akan dimulai dan hanya memiliki satu solusi yang unik. | ||
| + | |||
| + | Resume pertemuan kelima : resume | ||
| + | |||
| + | |||
| + | [[File:Pptassist3nbl1.JPG|800px]] | ||
| + | |||
| + | |||
| + | [[File:Pptassist3nbl2.JPG|800px]] | ||
| + | |||
| + | |||
| + | [[File:Pptassist3nbl3.JPG|800px]] | ||
| + | |||
| + | |||
| + | Tugas pertemuan kelima : Initial and bounday problem | ||
| + | |||
| + | Menggunakan metode RungeKutta untuk menemukan hasil dari persamaan differensial. | ||
| + | |||
| + | [[File:Rungekuttanbl5.png|800px]] | ||
| + | |||
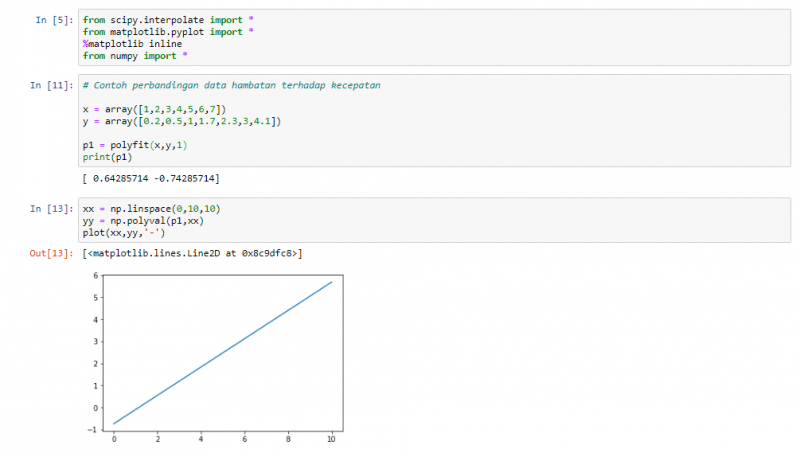
| + | Menggunakan regresi linear untuk menentukan hubungan antara hambatan dengan kecepatan kapal | ||
| + | |||
| + | [[File:Hambatan5nbl.png|800px]] | ||
| + | |||
| + | |||
| + | ==Pertemuan keenam== | ||
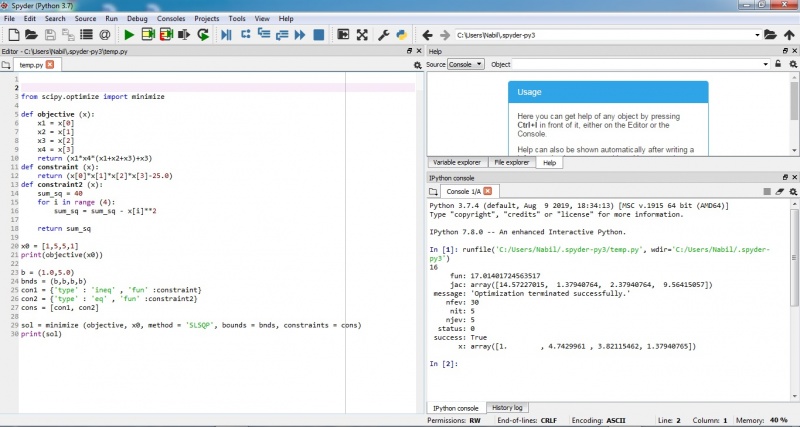
| + | Pertemuan keenam diisi oleh asisten dosen tentang optimasi. | ||
| + | |||
| + | Optimasi adalah suatu proses untuk mencapai hasil yang ideal atau optimasi (nilai efektif yang dapat dicapai). Optimasi dapat diartikan sebagai suatu bentuk mengoptimalkan sesuatu hal yang sudah ada, ataupun merancang dan membuat sesusatu secara optimal. | ||
| + | |||
| + | |||
| + | [[File:Pertemuan6nbl.jpg|800px]] | ||
| + | |||
| + | |||
| + | Tugas pertemuan keenam : Optimasi | ||
| + | |||
| + | |||
| + | [[File:Pertemuan6nbl2.jpg|800px]] | ||
| + | |||
| + | Tugas Video Optimasi | ||
| + | |||
| + | |||
| + | [[File:Videonblmetnum.mp4]] | ||
| + | |||
| + | |||
| + | ==Ujian Tengah Semester== | ||
| + | Berikut adalah link dari video ujian tengah semester metode numerik. | ||
| + | |||
| + | [https://www.youtube.com/watch?v=Yd-d7W8JIug video tugas ujian tengah semester metode numerik] | ||
Latest revision as of 23:02, 7 May 2020
Contents
Data Pribadi
Nama : M Nabil Arta
NPM : 1506734885
TTL : Jakarta, 18 Desember 1996
Jurusan : Teknik Perkapalan
Angkatan : 2015
Email : thenabilarta@gmail.com
Pengalaman Pemrograman
Kebetulan saya sudah menyelesaikan program skripsi tetapi masih ada mata kuliah yang belum selesai. Ketika skripsi, saya dibimbing dosen saya Pak Dr. Ir. Gunawan, M.Eng. untuk membuat sebuah program menggunakan bahasa C#. Program tersebut dibuat untuk memperkirakan tata letak komponen pada kamar mesin kapal seefisien mungkin.
Pertemuan Pertama
Pertemuan pertama kelas metode numerik ini diisi oleh perkenalan dosen yang akan mengajar kelas metode numerik yaitu Dr. Ir. Ahmad Indra Siswantara dan Prof.Dr. Ir. Harinaldi, M.Eng. dilanjutkan oleh langsung membuat halaman pada wiki.
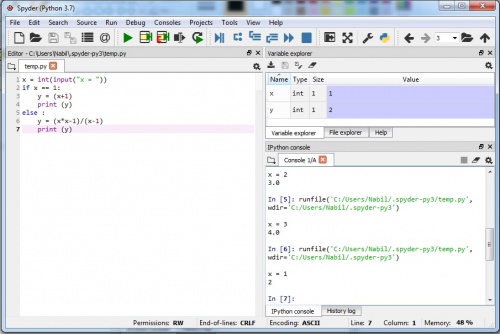
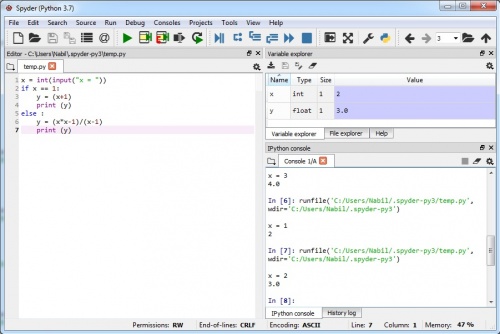
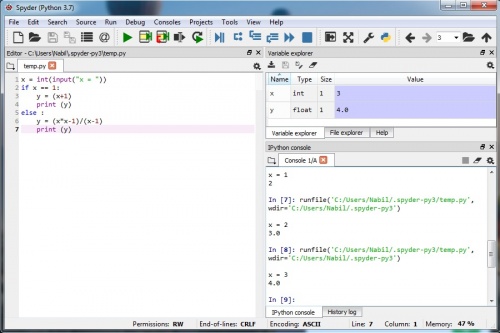
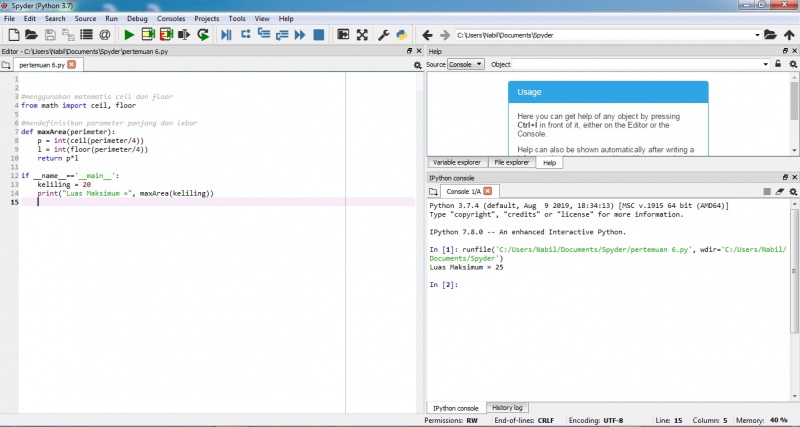
Tugas 1 : Menentukan nilai f(x)= x^2-1/x-1 dengan x=1
Menggunakan Phyton Spyder 3.7
Analisis:
Phyton terbukti dapat digunakan untuk menyelesaikan masalah perhitungan matematika sederhana. Penggunaan Phyton akan jauh lebih baik digunakan ketimbang perhitungan manual apabila melibatkan perhitungan yang banyak dan rumit. Akan tetapi, untuk dapat menyelesaikan persoalaan menggunakan Phyton, kita terlebih dahulu harus mempelajari bahasa pemrograman dari Phyton itu sendiri.
Pertemuan Kedua
Metode Numerik sangat baik untuk digunakan oleh mahasiswa atau orang-orang yang berkutat di ilmu pengetahuan karena kemampuannya menyelesaikan persoalan rumit apabila sudah mengerti bahasa pemrogramannya.
Ilmu metode numerik sangat menarik dan menyenangkan untuk dipelajari. Dengan mempelajari ilmu ini kita seharusnya semakin kagum dengan kebesaran Tuhan Yang Maha Esa. Diibaratkan seperti mencelupkan jari ke dalam lautan. Ketika jari kembali diangkat dari air, tetesan air dari jari tersebut adalah ilmu metode numerik dibandingkan dengan lautan yang merupakan ilmu pengetahuan sang pencipta.
Kita juga harus berjuang melawan KEM (Ketidaktahuan, Egois, dan Malas). Caranya adalah mendorong diri kita sendiri agar selalu menjadi pribadi yang lebih baik.
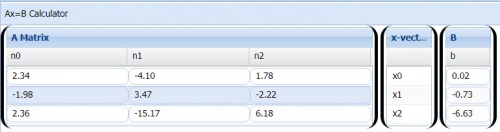
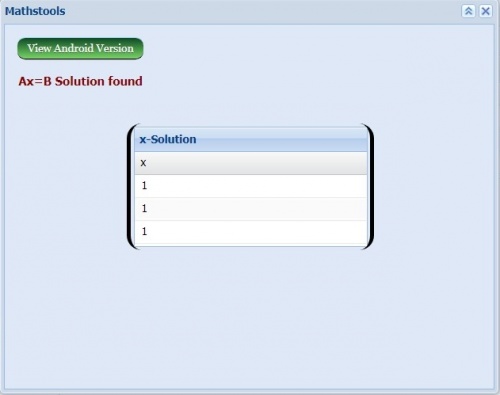
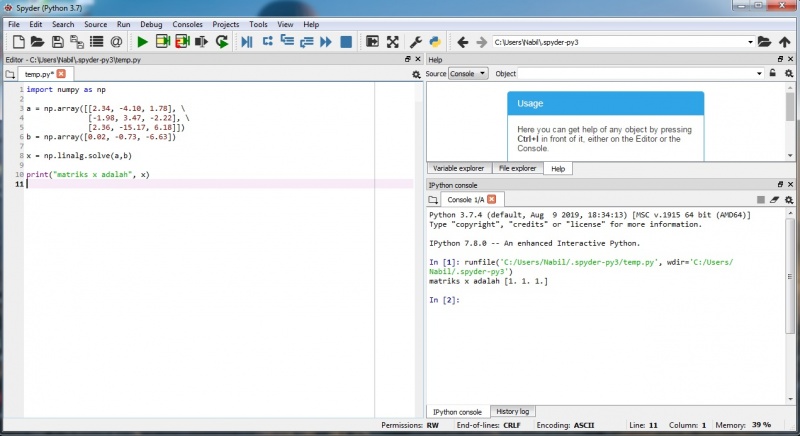
Tugas pertemuan kedua (1) : Penyelesaian matrix menggunakan Phyton
Tugas pertemuan kedua berkaitan dengan membahas soal tentang aljabar linear dan teori Newton Fisika diselesaikan dengan menggunakan Phyton.
Menggunakan kalkulator matrix didapatkan
Perhitungan matrix menggunakan Phyton Spyder
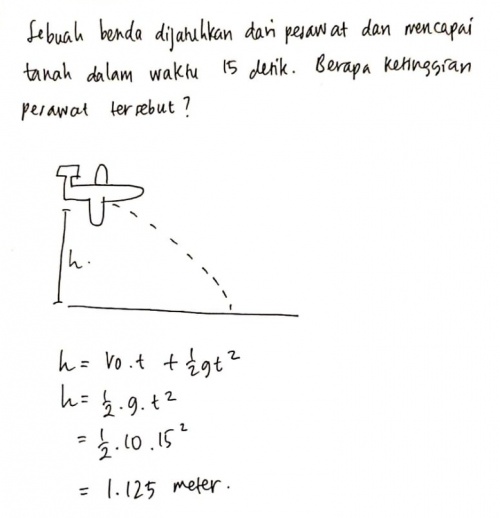
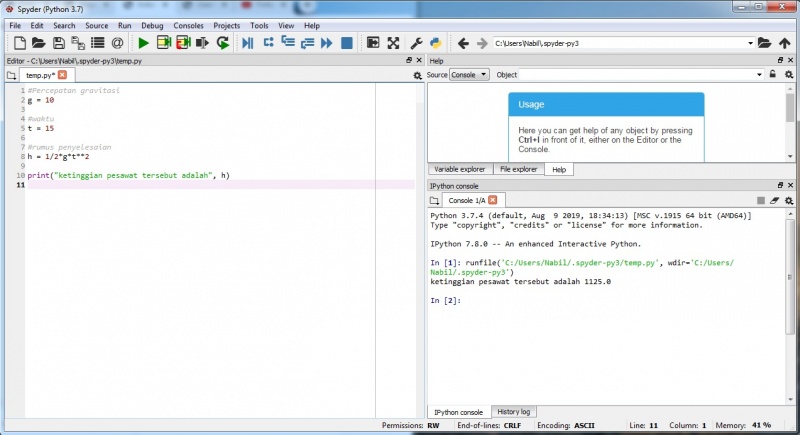
Tugas pertemuan kedua (2) : Initial Value Problem
Menyelesaikan soal yang berkaitan dengan GLBB gerak jatuh bebas di Phyton.
Dengan menggunakan Phyton Spyder
Tugas pertemuan kedua (3) : Power Point
Progres belajar metode numerik.
Pertemuan Ketiga
Semua rumus hanya berupa pendekatan karena tidak ada rumus atau simulasi yang akan sama dengan kejadian aslinya. Permodelan diantaranya yaitu : prinsip konservasi massa, hukum newton (F = m.a), hukum konservasi energi.
Mencari modul matematis dari pegas yaitu gerakan bolak-balik.
Tugas Asistensi : PPT Laporan Asistensi
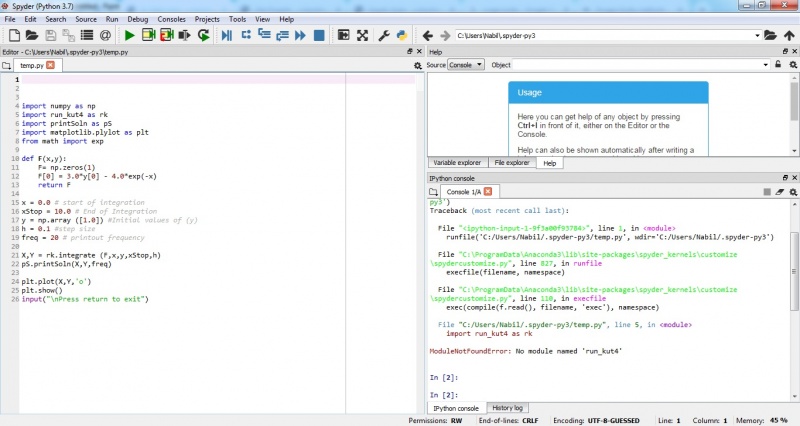
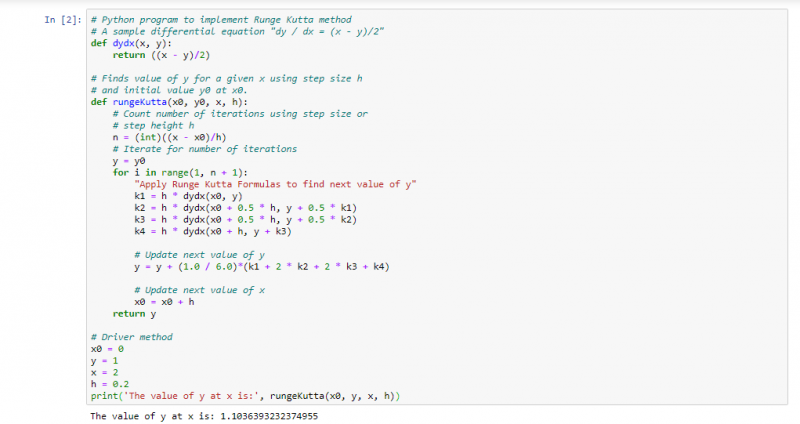
Tugas Aplikasi Runge-Kutta pada soal
Pertemuan Keempat
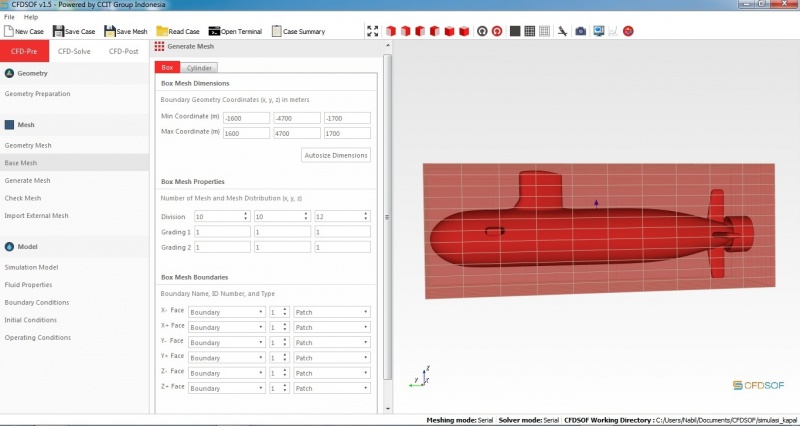
Pada pertemuan keempat, Pak Da'i menjelaskan tentang rumus-rumus. Rumus-rumus hanya merupakan pendekatan jadi tidak bisa dianggap bahwa rumus akan sepenuhnya menyamai kondisi keadaan sesungguhnya. Selanjutnya diisi dengan asistensi dengan sebuah program CFD yaitu program yang mensimulasikan sebuah kapal selam yang berada di dalam laut. Program tersebut menghitung hubungan fluida dengan kapal selam tersebut dengan variabel seperti hambatan, turbulensi, dan semacamnya.
Saya sudah mengikuti contoh yang disediakan di tutorial dan mengambil salah satu contoh file obj kapal selam dari internet. Saya sudah melakukan langkah yang sama seperti yang dilakukan pada tutorial akan tetapi saya belum dapat menghasilkan penyelesaian yang sama.
Pada sesi Asistensi, kami ditugaskan untuk mengubah grafik yang didapat menjadi lebih dapat dihitung dengan menggunakan regresi. Regresi itu sendiri dilakukan pada pemrograman Phyton.
Tugas pertemuan keempat : resume
Pertemuan kelima
Nilai merupakan ukuran performa dari seorang murid. Tujuan dasar metode numerik adalah kemampuan menyelesaikan konsep dalam perhitungan sederhana. Pada zaman sekarang sudah ada tiga cara memecahkan sebuah kasus yaitu dengan teori, numerik, dan eksperimen.
Perbedaan antara Boundary dan Initial Value Problem. Pada Boundary Value Problem kita tidak mengetahui apa yang terjadi di dalam proses tapi kita tahu batas-batasannya yang dievaluasi setiap waktu.
Initial Value problem kita tahu sesaat sebelum proses akan dimulai dan hanya memiliki satu solusi yang unik.
Resume pertemuan kelima : resume
Tugas pertemuan kelima : Initial and bounday problem
Menggunakan metode RungeKutta untuk menemukan hasil dari persamaan differensial.
Menggunakan regresi linear untuk menentukan hubungan antara hambatan dengan kecepatan kapal
Pertemuan keenam
Pertemuan keenam diisi oleh asisten dosen tentang optimasi.
Optimasi adalah suatu proses untuk mencapai hasil yang ideal atau optimasi (nilai efektif yang dapat dicapai). Optimasi dapat diartikan sebagai suatu bentuk mengoptimalkan sesuatu hal yang sudah ada, ataupun merancang dan membuat sesusatu secara optimal.
Tugas pertemuan keenam : Optimasi
Tugas Video Optimasi
Ujian Tengah Semester
Berikut adalah link dari video ujian tengah semester metode numerik.