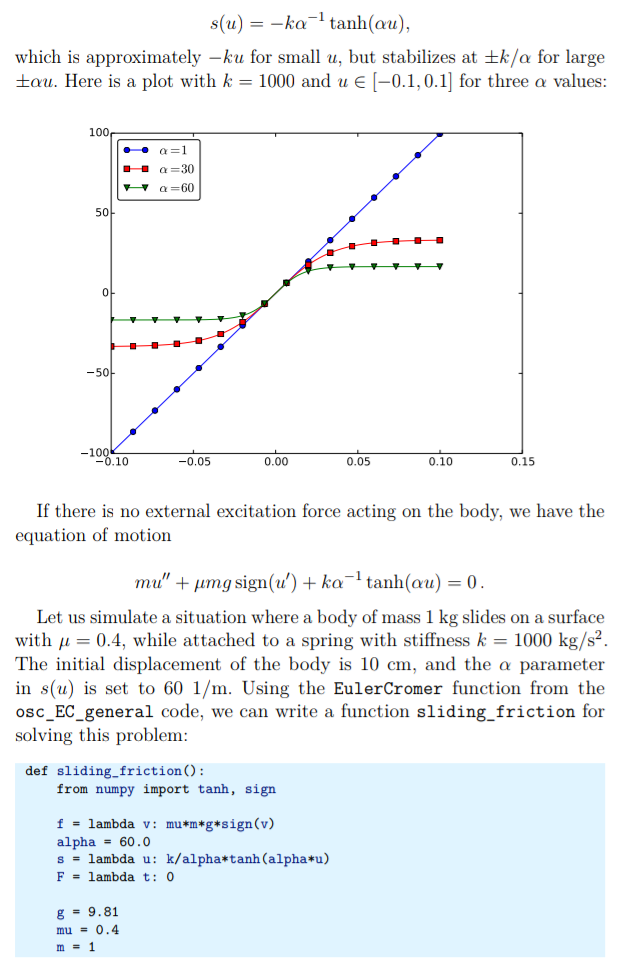
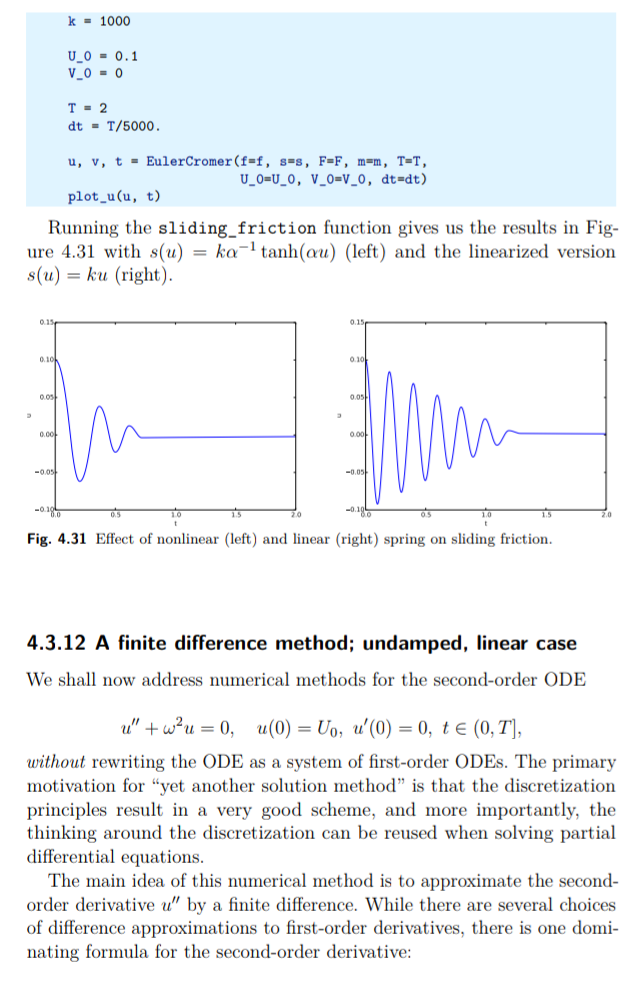
Difference between revisions of "Oscillating one-dimensional systems"
m (Reverted edits by Surya94aji (talk) to last revision by Ahmadzikri.engineer) |
(→4.3.1 Penurunan Model yang Sederhana) |
||
| Line 81: | Line 81: | ||
Banyak sistem keteknikan (''engineering'') berkaitan dengan osilasi, dan persamaan diferensial merupakan kunci utama untuk memahami, memprediksi, dan mengontrol osilasi. Kita mulai dengan model paling sederhana yang berkaitan dengan dinamika penting dari sistem osilasi. suatu benda dengan massa m melekat/dikaitkan pada pegas dan bergerak sepanjang garis tanpa gesekan, lihat Gambar 4.15 untuk sketsa (''rolling wheels'' menunjukkan “tidak ada gesekan”). Ketika pegas diregangkan (atau dikompresi), gaya pegas menarik (atau mendorong) bodi (penampang m) kembali dan bekerja "melawan" gerakan. Lebih tepatnya, misalkan x (t) adalah posisi bodi pada sumbu x, dimana bodi bergerak. Pegas tidak direntangkan ketika x= 0, sehingga gaya adalah nol, dan x= 0 karenanya posisi keseimbangan bodi. Gaya pegas adalah -kx, dimana k adalah konstanta yang diukur. Kami berasumsi bahwa tidak ada gaya lain (mis., Tidak ada gesekan). Hukum Newton ke-2 F=ma kemudian memiliki F=-kx dan a=x ̈ , | Banyak sistem keteknikan (''engineering'') berkaitan dengan osilasi, dan persamaan diferensial merupakan kunci utama untuk memahami, memprediksi, dan mengontrol osilasi. Kita mulai dengan model paling sederhana yang berkaitan dengan dinamika penting dari sistem osilasi. suatu benda dengan massa m melekat/dikaitkan pada pegas dan bergerak sepanjang garis tanpa gesekan, lihat Gambar 4.15 untuk sketsa (''rolling wheels'' menunjukkan “tidak ada gesekan”). Ketika pegas diregangkan (atau dikompresi), gaya pegas menarik (atau mendorong) bodi (penampang m) kembali dan bekerja "melawan" gerakan. Lebih tepatnya, misalkan x (t) adalah posisi bodi pada sumbu x, dimana bodi bergerak. Pegas tidak direntangkan ketika x= 0, sehingga gaya adalah nol, dan x= 0 karenanya posisi keseimbangan bodi. Gaya pegas adalah -kx, dimana k adalah konstanta yang diukur. Kami berasumsi bahwa tidak ada gaya lain (mis., Tidak ada gesekan). Hukum Newton ke-2 F=ma kemudian memiliki F=-kx dan a=x ̈ , | ||
| + | |||
| + | -kx = mẍ | ||
| + | |||
| + | Yang dapat ditulis sebagai | ||
| + | |||
| + | ẍ + w2x = 0 | ||
| + | |||
| + | Dengan w = (yang sangat umum) | ||
| + | |||
| + | Persamaan (4.42) adalah persamaan diferensial ordo kedua, dan karenanya kita membutuhkan dua kondisi awal, satu pada posisi x (0) dan satu lagi pada kecepatan x’(0). Disini kita memilih benda pada keadaan diam, namun bergerak dari posisi kesetimbangannya yaitu: | ||
| + | |||
| + | x(0) = X0, x’(0) = 0 | ||
| + | |||
| + | Solusi yang tepat dari persamaan (4.42) dengan kondisi awal ini adalah x(t) = X0 cos wt. Ini akan menjadi sangat mudah untuk diverifikasi dengan mensubstitusikan ke persamaan (4.42) dan mengecek kondisi awalnya. Solusi ini menyatakan bahwa sistem pegas-massa (spring-mass) berosilasi bolak-balik sebagaimana yang dijelaskan oleh kurva cosinus. | ||
== Artikel 1 Hasil diskusi : judul .. == | == Artikel 1 Hasil diskusi : judul .. == | ||
Revision as of 14:52, 10 April 2020
Contents
[hide]Studi kasus dan Terjemahan
Ref. Linge S, Langtangen HP, Programming for Computations - A Gentle Introduction to Numerical Simulations with Python
Terjemahan
4.3.1 Penurunan Model yang Sederhana
Banyak sistem keteknikan (engineering) berkaitan dengan osilasi, dan persamaan diferensial merupakan kunci utama untuk memahami, memprediksi, dan mengontrol osilasi. Kita mulai dengan model paling sederhana yang berkaitan dengan dinamika penting dari sistem osilasi. suatu benda dengan massa m melekat/dikaitkan pada pegas dan bergerak sepanjang garis tanpa gesekan, lihat Gambar 4.15 untuk sketsa (rolling wheels menunjukkan “tidak ada gesekan”). Ketika pegas diregangkan (atau dikompresi), gaya pegas menarik (atau mendorong) bodi (penampang m) kembali dan bekerja "melawan" gerakan. Lebih tepatnya, misalkan x (t) adalah posisi bodi pada sumbu x, dimana bodi bergerak. Pegas tidak direntangkan ketika x= 0, sehingga gaya adalah nol, dan x= 0 karenanya posisi keseimbangan bodi. Gaya pegas adalah -kx, dimana k adalah konstanta yang diukur. Kami berasumsi bahwa tidak ada gaya lain (mis., Tidak ada gesekan). Hukum Newton ke-2 F=ma kemudian memiliki F=-kx dan a=x ̈ ,
-kx = mẍ
Yang dapat ditulis sebagai
ẍ + w2x = 0
Dengan w = (yang sangat umum)
Persamaan (4.42) adalah persamaan diferensial ordo kedua, dan karenanya kita membutuhkan dua kondisi awal, satu pada posisi x (0) dan satu lagi pada kecepatan x’(0). Disini kita memilih benda pada keadaan diam, namun bergerak dari posisi kesetimbangannya yaitu:
x(0) = X0, x’(0) = 0
Solusi yang tepat dari persamaan (4.42) dengan kondisi awal ini adalah x(t) = X0 cos wt. Ini akan menjadi sangat mudah untuk diverifikasi dengan mensubstitusikan ke persamaan (4.42) dan mengecek kondisi awalnya. Solusi ini menyatakan bahwa sistem pegas-massa (spring-mass) berosilasi bolak-balik sebagaimana yang dijelaskan oleh kurva cosinus.