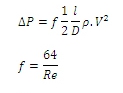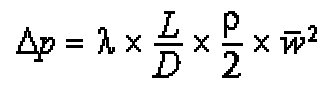Difference between revisions of "Mizan Eryandhika Guntorozi"
m |
|||
| Line 121: | Line 121: | ||
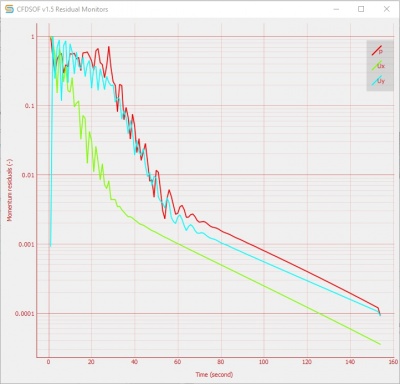
[[File:CFDSOF3_Mizan.jpg|400px|thumb|center|Berikut adalah residual monitor yang muncul]] | [[File:CFDSOF3_Mizan.jpg|400px|thumb|center|Berikut adalah residual monitor yang muncul]] | ||
| + | |||
[[File:CFDSOF7_Mizan.jpg|400px|thumb|center|Berikut adalah grafik dan tampilan pada Paraview]] | [[File:CFDSOF7_Mizan.jpg|400px|thumb|center|Berikut adalah grafik dan tampilan pada Paraview]] | ||
| − | == Pertemuan 2: Hukum Konservasi dan Vektor Aliran== | + | == Pertemuan 2: Hukum Konservasi dan Vektor Velocity Aliran== |
| − | '''Pertemuan 2: Hukum Konservasi dan Vektor Aliran; Rabu, 1 April 2020''' | + | '''Pertemuan 2: Hukum Konservasi dan Vektor Velocity Aliran; Rabu, 1 April 2020''' |
Pertemuan 2 dilaksanakan melalui aplikasi zoom pada hari tanggal Rabu, 1 April 2020 pada pukul 13.10 sampai dengan 15.02. Pertemuan 2 diisi oleh Pak Ahmad Indra Siswanto atau Pak DAI dan juga dilanjutkan oleh Pak Muhammad Hilman Gumelar Syafei atau Mas Edo selaku asisten dosen Pak Ahmad Indra Siswanto atau Pak DAI. Pertemuan 2 ini diawali dengan pemaparan materi dimana Pak DAI membahas tentang '''"Hukum Konservasi"''' yang dibagi menjadi tiga, yaitu Hukum Konservasi Massa, Konservasi Momentum dan Konservasi Energi seperti berikut: | Pertemuan 2 dilaksanakan melalui aplikasi zoom pada hari tanggal Rabu, 1 April 2020 pada pukul 13.10 sampai dengan 15.02. Pertemuan 2 diisi oleh Pak Ahmad Indra Siswanto atau Pak DAI dan juga dilanjutkan oleh Pak Muhammad Hilman Gumelar Syafei atau Mas Edo selaku asisten dosen Pak Ahmad Indra Siswanto atau Pak DAI. Pertemuan 2 ini diawali dengan pemaparan materi dimana Pak DAI membahas tentang '''"Hukum Konservasi"''' yang dibagi menjadi tiga, yaitu Hukum Konservasi Massa, Konservasi Momentum dan Konservasi Energi seperti berikut: | ||
1. Konservasi massa adalah apabila dalam suatu sistem massa total mengalami perubahan secara total artinya berubah terhadap jarak/ruang dan waktu, maka perubahan tersebut dapat diimplementasikan atau diasumsikan sama dengan 0. | 1. Konservasi massa adalah apabila dalam suatu sistem massa total mengalami perubahan secara total artinya berubah terhadap jarak/ruang dan waktu, maka perubahan tersebut dapat diimplementasikan atau diasumsikan sama dengan 0. | ||
| − | + | '''dm/dt = 0''' | |
2. Konservasi Momentum adalah apabila dalam suatu sistem kecepatan dan momentum berubah terhadap jarak/ruang dan waktu, maka perubahan tersebut dapat diimplementasikan dengan sigma F atau total gaya yang terjadi. | 2. Konservasi Momentum adalah apabila dalam suatu sistem kecepatan dan momentum berubah terhadap jarak/ruang dan waktu, maka perubahan tersebut dapat diimplementasikan dengan sigma F atau total gaya yang terjadi. | ||
| − | + | '''M. dV/dt = sigma''' | |
| − | 3. Konservasi Energi adalah apabila dalam suatu sistem energi total mengalami perubahan secara total artinya berubah terhadap jarak/ruang dan waktu, maka perubahan energi tersebut dapat diimplementasikan sebagai W atau kerja dan energi panas atau Q. | + | 3. Konservasi Energi adalah apabila dalam suatu sistem energi total mengalami perubahan secara total artinya berubah terhadap jarak/ruang dan waktu, maka perubahan energi tersebut dapat diimplementasikan sebagai W atau kerja dan energi panas atau Q. |
| − | + | '''dE/dt = W+Q''' | |
| − | |||
Dengan catatan: | Dengan catatan: | ||
| Line 157: | Line 157: | ||
Contoh Perhitungan Fluida terhadap Benda adalah kipas angin yang menggerakan fluida disekitarnya, kemudian muncul ''concern'' berapa daya yg diperlukan kipas angin untuk menggerakan fluida tersebut? Daya yang diperlukan kipas angin terjadi di dalam kipas angin tersebut dimana kipas angin merupakan suatu sistem. | Contoh Perhitungan Fluida terhadap Benda adalah kipas angin yang menggerakan fluida disekitarnya, kemudian muncul ''concern'' berapa daya yg diperlukan kipas angin untuk menggerakan fluida tersebut? Daya yang diperlukan kipas angin terjadi di dalam kipas angin tersebut dimana kipas angin merupakan suatu sistem. | ||
| − | + | '''Kemudian, Pak DAI menegaskan disitulah kenapa kita melakukan pendekatan volume bukan sistem.''' | |
| + | |||
| + | Pada pertemuan-2 kali ini, juga dijelaskan kembali pertanyaan yang sudah di lempar sebelumnya di pertemuan-1, yaitu konsep entrance region, entrance length dan fully develop flow pada aliran pipa seperti pada gambar di bawah ini. | ||
| + | |||
| + | [[File:fluida_mizan.jpg|400px|thumb|center|https://sbainvent.com/fluid-mechanics/fully-developed-flow/]] | ||
Selanjutnya, pertemuan dilanjutkan oleh Mas Edo dengan lemparan pertanyaan oleh Pak DAI. Mas Edo di minta untuk menuntun mahasiswa untuk kembali menggunakan aplikasi CFDSOF untuk kemudian mempelajari vektor aliran atas pertanyaan berikut ini: | Selanjutnya, pertemuan dilanjutkan oleh Mas Edo dengan lemparan pertanyaan oleh Pak DAI. Mas Edo di minta untuk menuntun mahasiswa untuk kembali menggunakan aplikasi CFDSOF untuk kemudian mempelajari vektor aliran atas pertanyaan berikut ini: | ||
| Line 163: | Line 167: | ||
[[File:pertanyaan_pertemuan2_mizan.jpg|400px|thumb|center|Pertanyaan yang mengacu pada pengerjaan CFDSOF]] | [[File:pertanyaan_pertemuan2_mizan.jpg|400px|thumb|center|Pertanyaan yang mengacu pada pengerjaan CFDSOF]] | ||
| − | Hal pertama yang dilakukan adalah, mereview ulang teknik-teknik pengerjaan CFDSOF pada Pertemuan 1: Aliran Viskos | + | Hal pertama yang dilakukan adalah, mereview ulang teknik-teknik pengerjaan CFDSOF pada Pertemuan 1: Aliran Viskos, Lalu Mas Edo membantu kami mahasiswa/i untuk mengerjakan permasalahan tersebut. |
| + | |||
| + | '''Jawaban''' untuk bentuk vektor kecepatan yang terjadi pada persoalan diatas adalah sebagai berikut, dengan menggunakan persamaan: | ||
| + | |||
| + | '''μ = 1/2.ρ.V^2''' | ||
| + | |||
| + | Dengan catatan: | ||
| + | |||
| + | ρ = Densitas fluida (g/cm^3 atau kg/m^3 | ||
| + | |||
| + | v = Kecepatan rata-rata fluida di dalam pipa (m/s atau cm/s) | ||
| + | |||
| + | μ = Viskositas (Pa) | ||
| + | |||
| + | Berikut ini, adalah '''grafik kecepatan dan tekanan''' yang didapatkan: | ||
| + | |||
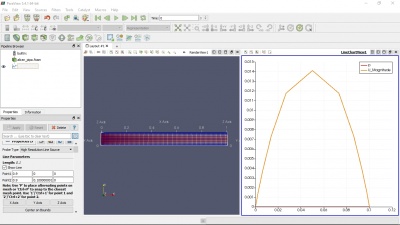
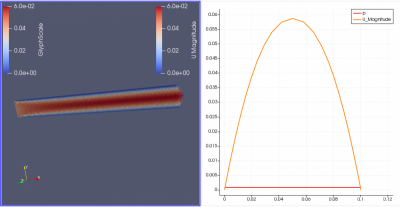
| + | [[File:lampiran_mizan_vector velocity.png|400px|thumb|center|Jawaban untuk soal poin a1 dan b1 (V=0,01 m/s dan μ=4x10^-5)]] | ||
| + | |||
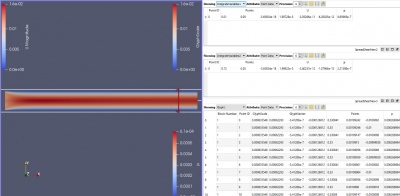
| + | [[File:lampiran_mizan_vector velocity_b.png|400px|thumb|center|Jawaban untuk soal poin a2 (V=0,01 m/s dan μ=10^-5)]] | ||
| + | |||
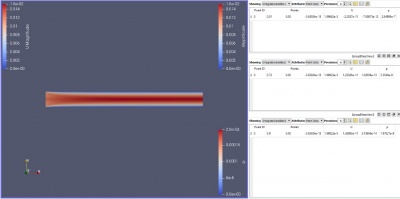
| + | [[File:lampiran_mizan_vector velocity_c.png|400px|thumb|center|Jawaban untuk soal poin b2 (V=0,04 m/s dan μ=4x10^-5)]] | ||
| + | |||
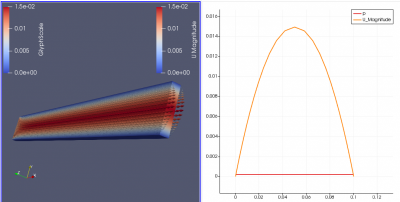
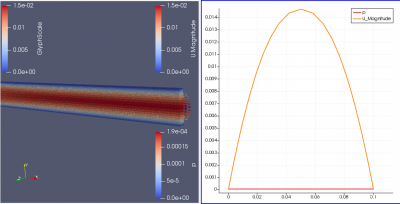
| + | Berikut ini, adalah '''perbandingan perubahan kecepatan''' yang terjadi: | ||
| + | |||
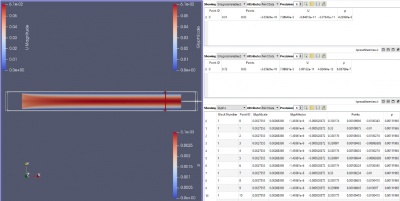
| + | [[File:lampiran_mizan_vector velocity_d.jpg|400px|thumb|center|Jawaban untuk soal poin a1 dan b1 (V=0,01 m/s dan μ=4x10^-5)]] | ||
| + | |||
| + | [[File:lampiran_mizan_vector velocity_e.jpg|400px|thumb|center|Jawaban untuk soal poin a2 (V=0,01 m/s dan μ=10^-5)]] | ||
| + | |||
| + | [[File:lampiran_mizan_vector velocity_f.jpg|400px|thumb|center|Jawaban untuk soal poin b2 (V=0,04 m/s dan μ=4x10^-5)]] | ||
Revision as of 12:18, 7 April 2020
Contents
Pendahuluan
بِسْمِ اللهِ الرَّحْمَنِ الرَّحِيْمِ
السَّلاَمُ عَلَيْكُمْ وَرَحْمَةُ اللهِ وَبَرَكَاتُهُ
Perkenalkan, nama saya Mizan Eryandhika Guntorozi atau yang biasa dipanggil Mizan, saya merupakan mahasiswa S1 Paralel Teknik Mesin Universitas Indonesia. Berikut adalah biodata diri saya dan juga catatan-catatan saya mengenai Perkuliahan Jarak Jauh(PJJ) mata kuliah Mekanika Fluida sampai dengan Ujian Akhir Semester(UAS). Catatan tersebut meliputi tugas yang diberikan pada setiap pertemuan juga progress pembelajaran saya setiap diadakan pertemuan. Saya berharap page ini dapat memberikan manfaat bagi siapapun yang membaca. Terimakasih.
Biodata diri
Nama: Mizan Eryandhika Guntorozi
NPM: 1806181823
Fakultas / Program Studi: Teknik / S1 Paralel Teknik Mesin
Pertemuan 1: Aliran Viskos
Pertemuan 1: Aliran Viskos ; Selasa, 31 Maret 2020
Pertemuan 1 dilaksanakan melalui aplikasi zoom pada hari tanggal Selasa, 31 Maret 2020 pada pukul 13.30 sampai dengan 15.20. Pertemuan 1 diisi oleh Pak Muhammad Hilman Gumelar Syafei atau yang akrab dipanggil Mas Edo selaku asisten dosen Pak Ahmad Indra Siswanto atau Pak DAI. Pertemuan 1 ini diawali dengan pemaparan materi "Aliran Viskos" dimana Mas Edo membahas Reynolds Number.
Reynolds Number adalah perbandingan suatu inersia fluida dengan dinding pipa yang menghasilkan suatu gesekan. Gesekan tadi menghambat laju aliran fluida di dalam pipa yang dapat pula disebut sebagai viskositas. Jadi Reynolds Number itu adalah perbandingan inersia atau badan fluida dengan viskositas pada pipa. Dimana, semakin besar Reynolds Number suatu fluida maka semakin Turbulen suatu Aliran Fluida, begitu pula jika semakin kecil Reynolds Number suatu fluida maka semakin Laminar suatu Aliran Fluida. Hal ini akan saya bahas berikutnya.
Re = ρ v D / μ
Dengan catatan:
Re = Reynolds Number
ρ = Densitas fluida (g/cm^3 atau kg/m^3
v = Kecepatan rata-rata fluida di dalam pipa (m/s atau cm/s)
D = Diameter dalam pipa (m atau cm)
μ = Viskositas (Pa)
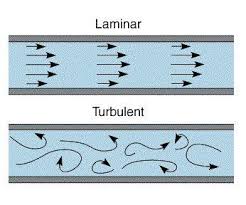
Kemudian, dari pernyataan Reynolds Number tadi, kita dapat concern mengenai Jenis-jenis Aliran suatu fluida dimana Mas Edo juga membahas hal tersebut yaitu Aliran Laminar dan Aliran Turbulen.
Aliran Laminar adalah aliran fluida yang bergerak dengan kondisi lapisan-lapisan yang membentuk garis-garis alir dan tidak berpotongan satu sama lain. Alirannya relatief mempunyai kecepatan rendah dan fluidanya bergerak sejajar
Aliran Turbulen adalah aliran fluida yang partikel-partikelnya bergerak secara acak dan tidak stabil dengan kecepatan relatif tinggi yang saling interaksi satu sama lain. Akibat dari hal tersebut garis alir antar partikel fluidanya saling berpotongan.
Dengan catatan:
- Aliran Laminar terjadi apabila Reynolds Number kurang dari 2200 Re < 2200
- Aliran Transisi terjadi apabila Reynolds Number sama dengan 2200 Re = 2200
- Aliran Turbulent terjadi apabila Reynolds Number lebih dari 2200 Re > 2200
Lalu, dari hal-hal yang telah di bahas tadi, maka memicu pertanyaan seperti berikut:
Pertanyaan:
1. Apa itu entrance region/aliran masuk?
2. Apa itu fully developed flow/aliran berkembang sempurna?
3. Apa itu entrance length?
4. Apa pengaruh viskositas? dan pengaruh pressure drop dalam pipa?
5. Bagaimana cara menghitung pressure drop suatu aliran dalam laminar/turbulen?
Jawaban:
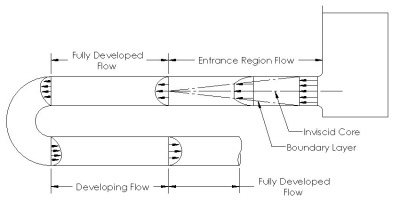
1. Entrance Region atau aliran masuk adalah area pintu masuk saluran fluida sesuai pada gambar yang diberikan. Entrance Region adalah bagian saluran di mana kecepatan dan/atau suhu tidak sepenuhnya berkembang. Entrance Region juga hanya bergantung pada kondisi awal atau kondisi masuknya fluida ke dalam pipa di mana lapisan batas meningkat hingga mengisi seluruh bagian melintang pipa.
2. Fully Developed Flow atau aliran berkembang sempurna adalah fase setelah selesainya fluida melewati Entrance Region. Dimana aliran ini terjadi ketika efek viskos atau efek gesekan fluida dengan dinding pipa akibat tegangan geser, yang kemudian menciptakan profil kecepatan yang berkembang sepenuhnya. Fully Developed Flow ini terjadi ketika fluida berjalan melalui pipa yang penampangnya lurus. Selain itu, kecepatan fluida untuk Fully Developed Flow titik tercepatnya adalah di garis tengah pipa.
3. Entrance length adalah jarak yang ditempuh aliran fluida setelah memasuki pipa tepat sebelum aliran berkembang sepenuhnya atau dapat disebut juga jarak ketika aliran masuk Entrance Region sampai sebelum masuk ke Fully Developed Flow.
4. Semakin meningkat densitas dan viskositas maka rata-rata kecepatan fluida semakin rendah. Hal tersebut mengacu kepada Pressure Drop yang merupakan penurunan tekanan dari satu titik di dalam sistem. Semakin meningkat viskositas dan semakin menurun densitas maka kondisi Fully Developed Flow semakin cepat tercapai di dalam suatu pipa horizontal.
5. Untuk Aliran Laminar:
Dengan Catatan:
Re = Reynolds Number
v = Kecepatan Aliran
D = Diameter Pipa
V = Kinematika Viskositas
λ = Koefisien Gesekan Pipa
Untuk Aliran Turbulen:
Dengan Catatan:
Δp = Pressure Drop
λ = Koefisien Gesekan Pipa
L = Panjang Pipa
D = Diameter Pipa
p = Kepadatan
v = Kecepatan aliran
Pertemuan dilanjutkan dengan tutorial cara menggunakan aplikasi CFDSOF. CFDSOF ini merupakan aplikasi untuk melakukan simulasi aliran fluida dalam suatu media. Tutorial CFDSOF yang dipimpin oleh Mas Edo ini cukup jelas. Beliau menjelaskan cara menggunakan aplikasi ini dengan baik dan benar. Aplikasi CFDSOF ini juga cukup membantu para pengguna untuk menggambarkan simulasi aliran fluida serta membantu perhitungan untuk selanjutnya diaplikasikan di lapangan. CFDSOF ini juga cukup fleksibel apabila pengguna ingin membuat simulasi dalam bentuk box atau dalam bentuk cylinder dan kemudian dapat diatur dimensinya sesuai yang pengguna inginkan.
Pada CFDSOF kami diajarkan untuk membuat simulasi aliran laminar dengan mengaplikasikan aliran viscous pada CFDSOF. Pertama-tama, hal yang dilakukan adalah menentukan wall, inflow, outflow pada tampilan bidang xyz. Kemudian menentukan mesh pada bidang xyz, menentukan boundary dan terakhir melakukan simulasi dengan menekan tombol pada solver dan dapat dilihat hasilnya seperti pada Lampiran dibawah.
Lampiran
Pertemuan 2: Hukum Konservasi dan Vektor Velocity Aliran
Pertemuan 2: Hukum Konservasi dan Vektor Velocity Aliran; Rabu, 1 April 2020
Pertemuan 2 dilaksanakan melalui aplikasi zoom pada hari tanggal Rabu, 1 April 2020 pada pukul 13.10 sampai dengan 15.02. Pertemuan 2 diisi oleh Pak Ahmad Indra Siswanto atau Pak DAI dan juga dilanjutkan oleh Pak Muhammad Hilman Gumelar Syafei atau Mas Edo selaku asisten dosen Pak Ahmad Indra Siswanto atau Pak DAI. Pertemuan 2 ini diawali dengan pemaparan materi dimana Pak DAI membahas tentang "Hukum Konservasi" yang dibagi menjadi tiga, yaitu Hukum Konservasi Massa, Konservasi Momentum dan Konservasi Energi seperti berikut:
1. Konservasi massa adalah apabila dalam suatu sistem massa total mengalami perubahan secara total artinya berubah terhadap jarak/ruang dan waktu, maka perubahan tersebut dapat diimplementasikan atau diasumsikan sama dengan 0.
dm/dt = 0
2. Konservasi Momentum adalah apabila dalam suatu sistem kecepatan dan momentum berubah terhadap jarak/ruang dan waktu, maka perubahan tersebut dapat diimplementasikan dengan sigma F atau total gaya yang terjadi.
M. dV/dt = sigma
3. Konservasi Energi adalah apabila dalam suatu sistem energi total mengalami perubahan secara total artinya berubah terhadap jarak/ruang dan waktu, maka perubahan energi tersebut dapat diimplementasikan sebagai W atau kerja dan energi panas atau Q.
dE/dt = W+Q
Dengan catatan:
d = differensial total
dho = differensial parsial
Pak DAI kemudian bertanya bahwa pada mata kuliah Mekanika Fluida concern yang ada adalah menganalisis gerakan fluida terhadap benda atau sebaliknya gerakan benda terhadap fluida?
Pertanyaan tersebut dapat dijawab sebagai berikut:
-Perhitungan Benda terhadap Fluida
Contoh Peritungan Benda terhadap Fluida adalah aerodinamika, kemudian muncul concern apa akibat yang terjadi jika mobil melewati angin?. Jawab, yang terjadi adalah pada akhirnya terjadi hambatan oleh angin yang menghambat laju dari mobil. Disini, yang kita amati adalah fluida di sekitar mobil yaitu (volume control disekitar mobil).
-Perhitungan Fluida terhadap Benda
Contoh Perhitungan Fluida terhadap Benda adalah kipas angin yang menggerakan fluida disekitarnya, kemudian muncul concern berapa daya yg diperlukan kipas angin untuk menggerakan fluida tersebut? Daya yang diperlukan kipas angin terjadi di dalam kipas angin tersebut dimana kipas angin merupakan suatu sistem.
Kemudian, Pak DAI menegaskan disitulah kenapa kita melakukan pendekatan volume bukan sistem.
Pada pertemuan-2 kali ini, juga dijelaskan kembali pertanyaan yang sudah di lempar sebelumnya di pertemuan-1, yaitu konsep entrance region, entrance length dan fully develop flow pada aliran pipa seperti pada gambar di bawah ini.
Selanjutnya, pertemuan dilanjutkan oleh Mas Edo dengan lemparan pertanyaan oleh Pak DAI. Mas Edo di minta untuk menuntun mahasiswa untuk kembali menggunakan aplikasi CFDSOF untuk kemudian mempelajari vektor aliran atas pertanyaan berikut ini:
Hal pertama yang dilakukan adalah, mereview ulang teknik-teknik pengerjaan CFDSOF pada Pertemuan 1: Aliran Viskos, Lalu Mas Edo membantu kami mahasiswa/i untuk mengerjakan permasalahan tersebut.
Jawaban untuk bentuk vektor kecepatan yang terjadi pada persoalan diatas adalah sebagai berikut, dengan menggunakan persamaan:
μ = 1/2.ρ.V^2
Dengan catatan:
ρ = Densitas fluida (g/cm^3 atau kg/m^3
v = Kecepatan rata-rata fluida di dalam pipa (m/s atau cm/s)
μ = Viskositas (Pa)
Berikut ini, adalah grafik kecepatan dan tekanan yang didapatkan:
Berikut ini, adalah perbandingan perubahan kecepatan yang terjadi: