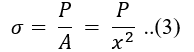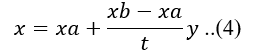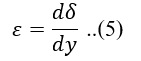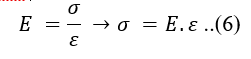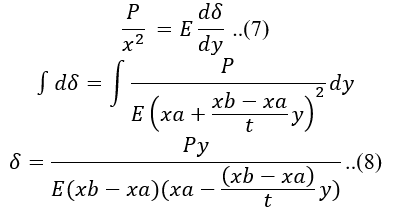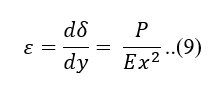Difference between revisions of "Tugas 2 ismail"
Ismailbagus (talk | contribs) (Jawaban) |
Ismailbagus (talk | contribs) (→Dijawab) |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 50: | Line 50: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">Gambar 2. Free body diagram pondasi</div> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;">Gambar 2. Free body diagram pondasi</div> | ||
| + | |||
| + | Sehingga tegangan normal yang diterima oleh pondasi dapat dirumuskan sebagai berikut: | ||
| + | |||
| + | [[file:Pers_3_-_ismail.png|center]] | ||
| + | |||
| + | dengan A adalah luas permukaan pondasi dan x adalah sisi permukaan pondasi. Sedangkan x merupakan fungsi dari y, yaitu: | ||
| + | |||
| + | [[file:WINWORD_2019-02-18_19-39-33.png|center]] | ||
| + | |||
| + | |||
| + | Adanya gaya aksial yang diterima pondasi membuat terjadinya regangan pada pondasi tersebut. Persamaan regangan pada pondasi dapat dirumuskan sebagai berikut: | ||
| + | |||
| + | [[file:WINWORD_2019-02-18_19-41-14.png|center]] | ||
| + | |||
| + | dimana, δ adalah ''displacement''. | ||
| + | |||
| + | |||
| + | Hukum Hooke menjelaskan bahwa rasio tegangan dan regangan disebut sebagai modulus elastisitas, persamaannya adalah: | ||
| + | |||
| + | [[file:WINWORD_2019-02-18_19-41-59.png|center]] | ||
| + | |||
| + | Substitusi persamaan (3), (5) dan (6) didapatkan persamaan untuk ''displacement'': | ||
| + | |||
| + | [[file:WINWORD_2019-02-18_19-44-05.png|center]] | ||
| + | |||
| + | Dengan cara yang sama, substitusi persamaan (5) dan (7) didapatkan persamaan untuk regangan sebagai berikut: | ||
| + | |||
| + | [[file:WINWORD_2019-02-18_19-44-54.png|center]] | ||
| + | |||
| + | ---- | ||
| + | |||
| + | ====Komputasi dengan EES==== | ||
| + | Persamaan yang telah didapat, yaitu tegangan (persamaan (3)), regangan (persamaan (8)) dan displacement (9), kemudian dibawa ke software pembantu EES. Adapun script yang digunakan adalah: | ||
| + | |||
| + | m=100 | ||
| + | g=9.87 | ||
| + | E=20*10^9 | ||
| + | xa=0.5 | ||
| + | xb=1 | ||
| + | t=0.7 | ||
| + | n=15 | ||
| + | F=m*g | ||
| + | P=F/4 | ||
| + | Posisi[1]=0 | ||
| + | duplicate i=1,15 | ||
| + | Posisi[i+1]=Posisi[i]+0.05 | ||
| + | Tegangan[i]=P/((xa+((xb-xa)/t)*Posisi[i])^2) | ||
| + | Regangan[i]=P/(E*((xa+((xb-xa)/t)*Posisi[i])^2)^2) | ||
| + | Displacement[i]=(P*posisi[i])/(E*(xb-xa)*(xa-(((xb-xa)/t)*Posisi[i]))) | ||
| + | End | ||
| + | |||
| + | Dari hasil simulasi didapatkan hasil sebagai berikut: | ||
| + | |||
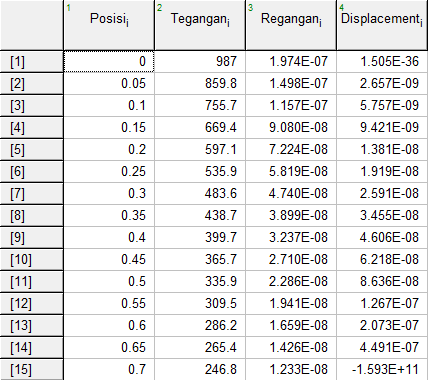
| + | Tabel 1. Hasil Perhitungan Menggunakan EES | ||
| + | |||
| + | [[file:EES_2019-02-18_07-07-53.png|center]] | ||
| + | |||
| + | ---- | ||
Latest revision as of 19:48, 18 February 2019
Contents
Soal
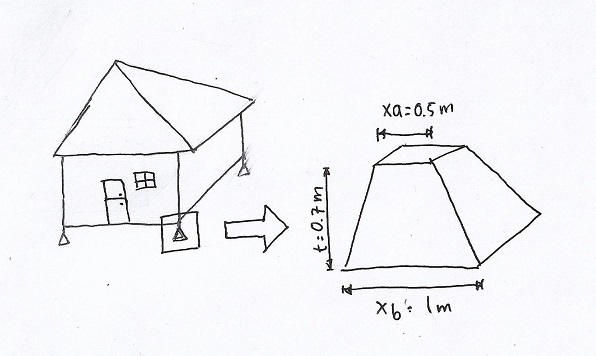
Bila diketahui rumah panggung berbentuk persegi empat dengan massa 100 kg, memiliki 4 pondasi di setiap ujung titik rumah. Bila diketahui pondasi berbentuk piramida sama kaki dengan sisi alas atas 0.5 m, sisi alas bawah 1 m, tinggi piramida 0.7 m, dan modulus elastisitas beton 20 x 109 Pa. Hitung displacement (δ), regangan (ε), dan tegangan (σ) pada pondasi!
Jawaban
Diketahui
- m = 100 kg
- xa = 0.5 m
- xb = 1 m
- t = 0.7 m
- E = 20 x 109 Pa
Asumsi
- g = 9.87 m/s^2
- gaya hanya mengarah ke satu arah (sumbu y/aksial)
- beton homogen
- beban yang diberikan oleh rumah panggung terhadap pondasi sama rata
Dijawab
Analisis
Pertama, dicari beban yang dimiliki oleh rumah panggung,
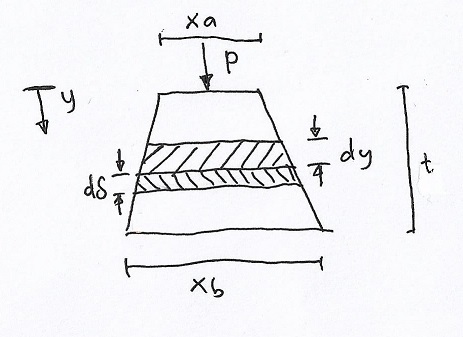
Karena beban yang diberikan terhadap pondasi sama rata, maka gaya yang diterima oleh satu pondasi adalah,
Sehingga tegangan normal yang diterima oleh pondasi dapat dirumuskan sebagai berikut:
dengan A adalah luas permukaan pondasi dan x adalah sisi permukaan pondasi. Sedangkan x merupakan fungsi dari y, yaitu:
Adanya gaya aksial yang diterima pondasi membuat terjadinya regangan pada pondasi tersebut. Persamaan regangan pada pondasi dapat dirumuskan sebagai berikut:
dimana, δ adalah displacement.
Hukum Hooke menjelaskan bahwa rasio tegangan dan regangan disebut sebagai modulus elastisitas, persamaannya adalah:
Substitusi persamaan (3), (5) dan (6) didapatkan persamaan untuk displacement:
Dengan cara yang sama, substitusi persamaan (5) dan (7) didapatkan persamaan untuk regangan sebagai berikut:
Komputasi dengan EES
Persamaan yang telah didapat, yaitu tegangan (persamaan (3)), regangan (persamaan (8)) dan displacement (9), kemudian dibawa ke software pembantu EES. Adapun script yang digunakan adalah:
m=100 g=9.87 E=20*10^9 xa=0.5 xb=1 t=0.7 n=15 F=m*g P=F/4 Posisi[1]=0 duplicate i=1,15 Posisi[i+1]=Posisi[i]+0.05 Tegangan[i]=P/((xa+((xb-xa)/t)*Posisi[i])^2) Regangan[i]=P/(E*((xa+((xb-xa)/t)*Posisi[i])^2)^2) Displacement[i]=(P*posisi[i])/(E*(xb-xa)*(xa-(((xb-xa)/t)*Posisi[i]))) End
Dari hasil simulasi didapatkan hasil sebagai berikut:
Tabel 1. Hasil Perhitungan Menggunakan EES