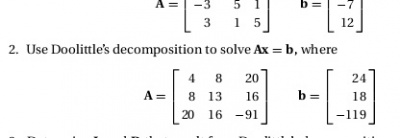Difference between revisions of "Sultan alif zidane"
Sultan.alif (talk | contribs) (→Pertemuan 2 Tanggal 14 Februari 2020) |
Sultan.alif (talk | contribs) (→Pertemuan 2 Tanggal 14 Februari 2020) |
||
| Line 65: | Line 65: | ||
== Pertemuan 2 Tanggal 14 Februari 2020 == | == Pertemuan 2 Tanggal 14 Februari 2020 == | ||
| − | + | Melawan KEM (Ketidaktahuan, Egois, Malas) | |
Ilmu itu ibaratkan mencelup jari kelingking di lautan luas, lalu tarik kembali dan akan ada tetesan. Maka tetesan itu ibarat ilmu kita di luasnya lautan ilmu. | Ilmu itu ibaratkan mencelup jari kelingking di lautan luas, lalu tarik kembali dan akan ada tetesan. Maka tetesan itu ibarat ilmu kita di luasnya lautan ilmu. | ||
| Line 82: | Line 82: | ||
| − | '''Initial Value | + | '''Initial Value Problem''' |
Revision as of 17:35, 14 February 2020
Sultan Alif Zidane merupakan salah seorang mahasiswa teknik perkapalan FTUI angkatan 2018. Sultan Alif Zidane biasa juga dipanggil sebagai Sultan. Sultan berasal dari kota Depok dan tinggal di kota tersebut sejak lahir.
Contents
Biodata
Nama: Sultan Alif Zidane
Tempat Lahir: Bogor
Usia: 19 Tahun
Alamat: Perumahan PGRI Blok E1/no:2, Cilodong, Depok, Jawa Barat
Jenis kelamin: Laki-laki
Agama: Islam
Kewarganegaraan: Indonesia
email: sultanalif2503@gmail.com
Pengalaman Programming
Sultan Alif Zidane tidak memiliki pengalaman dalam hal advance programming, dan belum pernah mencoba sesuatu mengenai advance programming. Namun dalam penggunaan beberapa aplikasi dalam hal pendidikan sudah beberapa kali menggunakan seperti MaxSurf ataupun Excel. Selain itu untuk bidang komputer, sultan hanya dapat menggunakan aplikasi tanpa melakukan pengembangan dalam suatu aplikasi. Bahkan laman ini merupakan laman pertama yang sultan buat, sultan belum pernah membuat blog atau hal semacamnya. Sehingga dapat dikatakan sultan masih menjadi pengguna dan belum mencapai titik menguasai.
Link Tugas
Tugas 1 Metnum Sultan Alif Zidane
Tugas 1 Metode Numerik
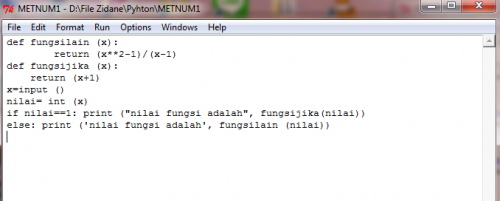
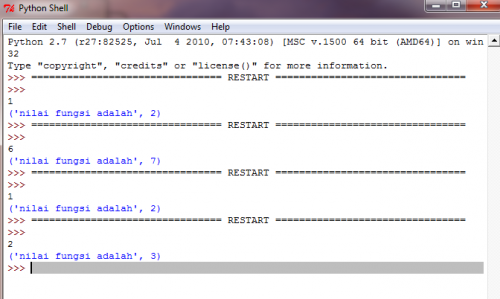
Selesaikan persamaan F(x)=(x^2-1)/(x-1)jika x=1
- Perhitungan Manual
Saat melakukan menggunakan perhitungan manual digunakan metode limit untuk mendapatkan jawaban yang tepat. Karena jika disubtitusi langsung akan mendapat jawaban 0/0 yang mana bukan merupakan penyelesaian dari persamaan matematik tersebut.
- Perhitungan menggunakan Komputer
Dari hasil perhitungan menggunakan komputer juga didapatkan hasil yang sama. Namun dalam prosesnya diperlukan perintah yang khusus dan spesifik. Sehingga perlu dilakukan pendalaman lebih lanjut dalam penggunaannya. Untuk cara menggunakan aplikasi pyhton sendiri dapat dipelajari di internet atau buku-buku yang ada.
Proses menghitung menggunkan aplikasi pyhton:
1. mengetik rumusan awal yaitu: def namafungsi (variabel):
2. dilanjut dengan mengetik return (fungsi secara matematis) untuk memasukan nilai variabel ke fungsi
3. mengetik kemungkinan fungsi lain, dalam hal ini fungsi yang diperoleh dari hasil limit.
4. mengetik nilai yang akan diinput ke dalam persamaan, dengan menggunakan integer agar dapat memasukan nilai menggunakan bilangan dan bukan kata-kata
5. memaasukan rumusan kemungkinan hasil yang diperoleh dari kedua persamaaan. dimana jika nilai yang dimasukan sama dengan 1 maka akan digunakan rumus yang diperoleh dari hasil limit.
Pertemuan 2 Tanggal 14 Februari 2020
Melawan KEM (Ketidaktahuan, Egois, Malas)
Ilmu itu ibaratkan mencelup jari kelingking di lautan luas, lalu tarik kembali dan akan ada tetesan. Maka tetesan itu ibarat ilmu kita di luasnya lautan ilmu.
metode numerik dapat digunakan untuk menyelesaikan masalah-masalah matematis.
setelah membaca ebook Numerical Methods in Engineering with Python 3, ada soal yang membuat saya tertarik dari ebook adalah soal no 2 dari problem set 2.2 System of Linear Algebraic Equations. Soal tersebut menjelaskan mengenai doolitle's decomposition dimana Ax=b, saya memilih soal ini karena saya tertarik mengenai metode numerik dalam penyelesaian persoalan dalam persamaan AlJabar.
Sumber gambar: Kiusalaas, Jaan. 2013. Numerical Methods in Engineering with Python 3. Cambridge: Cambridge University Press.
Initial Value Problem