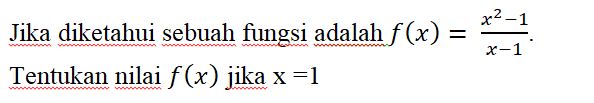Arief Muhammad Allydito

alt text

Arief Muhammad Allydito, lahir di Jakarta pada 4 Mei 20 tahun yang lalu. Saat ini merupakan mahasiswa semester empat jurusan Teknik Perkapalan Fakultas Teknik Universitas Indonesia angkatan 2018. Bersamaan dengan saya menulis, diperkenalkan pula salah satu Mata Kuliah di semester empat ini. Metode Numerik.

Merupakan mahasiswa yang berasal dari DKI Jakarta yang memiliki ketertarikan cukup tinggi terhadap membaca artikel.

Pada mata kuliah Metode Numerik ini, saya hanya mengetahui tentang sedikit dari bermacam-macam bahasa pemrograman. Hingga saat ini saya tidak pernah mempunyai pengalaman menggunakan bahasa pemrograman apapun, tetapi saya cukup memahami cara kerja dasar dari sebuah komputer dan internet. Swelama empat semester berjalan, saya cukup familiar dengan software Ms. Excel karena beberapa mata kuliah menggunakannya untuk membantu perhitungan. Kemudian saya juga cukup mengenal software design MaxSurf dan AutoCAD, karena di mata kuliah Tugas Merancang Kapal cukup sering digunakan.

Tugas Metode Numerik 1

alt text

Jika menggunakan metode manual, ketika nilai x di substitusi, hasilnya adalah "Tidak Terdefinisi". Kemudian jika menggunakan metode limit, didapati nilai x = 2

alt text

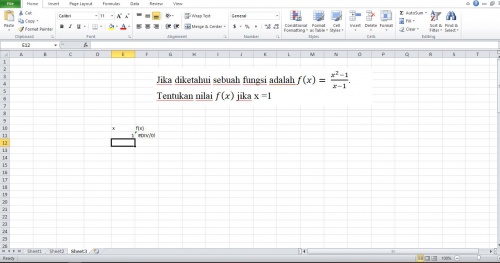
Dengan menggunakan metode perhitungan dengan Ms. Excel, ketika nilai x langsung di substitusikan ke fungsi, hasilnya pun juga menjadi "Tidak Terdefinisikan"

alt text

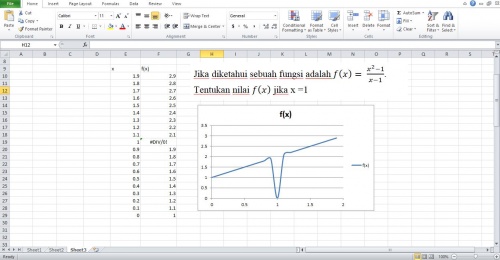
Tetapi, dengan menggunakan pendekatan limit. Hasilnya akan menuju ke sebuah nilai. Dengan memasukknya nilai x mulai dari 1.9 hingga 0 didapati bahwa nilai nya menuju ke "2" dari dengan pendekatan dari sisi kanan serta sisi kiri. Hasil akan lebih presisi jika dimasukkan lebih banyak variabel x.

alt text