Difference between revisions of "Tugas 1 Muhammad Attaritsabitsah Gibran"
(Created page with "== Cara Manual == File:METNUM TUGAS1 MANUAL MUHAMMAD ATTARITSABITSAH GIBRAN.png.jpg === Komentar === Pada masalah yang diberikan (persamaan matematika), saya menganalisa...") |
(→Cara Manual) |
||
| Line 1: | Line 1: | ||
== Cara Manual == | == Cara Manual == | ||
| − | [[File:METNUM TUGAS1 MANUAL MUHAMMAD ATTARITSABITSAH GIBRAN.png.jpg]] | + | [[File:METNUM TUGAS1 MANUAL MUHAMMAD ATTARITSABITSAH GIBRAN.png.jpg|600px]] |
=== Komentar === | === Komentar === | ||
| Line 6: | Line 6: | ||
Hal tersebut berarti nilai x=1 tidak memiliki hasil secara pasti. Bila digambarkan dalam grafik maka dilambangkan dengan lingkaran kosong. Yang berarti nilai tidak terdefinisi. Akan tetapi, kita selalu bisa mencari nilai terdekat dari nilai x=1. Nilai terdekat tersebut bisa saja sebelum atau sesudah x=1. Maka nilai x akan diganti dengan nilai terdekat tersebut. Konsep ini adalah konsep Limit. Dalam hal ini Limit f(x) degan nilai x mendekati 1. | Hal tersebut berarti nilai x=1 tidak memiliki hasil secara pasti. Bila digambarkan dalam grafik maka dilambangkan dengan lingkaran kosong. Yang berarti nilai tidak terdefinisi. Akan tetapi, kita selalu bisa mencari nilai terdekat dari nilai x=1. Nilai terdekat tersebut bisa saja sebelum atau sesudah x=1. Maka nilai x akan diganti dengan nilai terdekat tersebut. Konsep ini adalah konsep Limit. Dalam hal ini Limit f(x) degan nilai x mendekati 1. | ||
| + | |||
| + | == Cara Komputasi == | ||
| + | |||
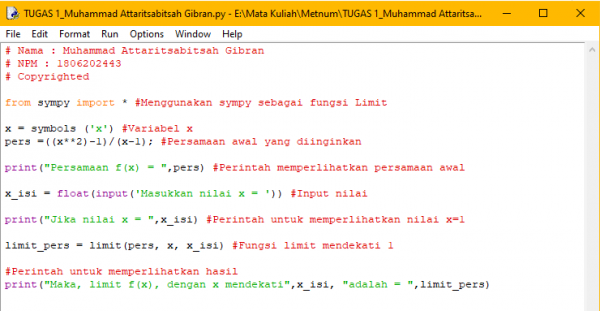
| + | === Python Code === | ||
| + | [[File:METNUM TUGAS1 MUHAMMAD ATTARITSABITSAH GIBRAN.png|600px]] | ||
| + | |||
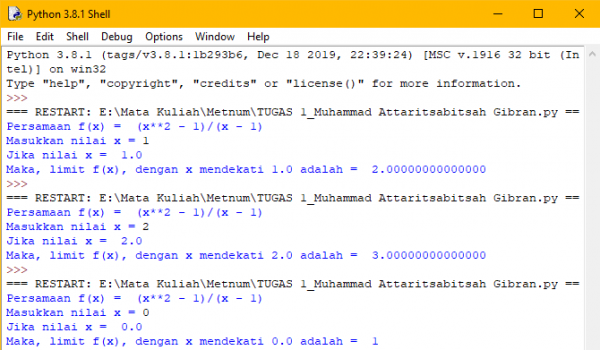
| + | === Hasil Run === | ||
| + | [[File:METNUM TUGAS1 2 MUHAMMAD ATTARITSABITSAH GIBRAN.png|600px]] | ||
| + | |||
| + | === Komentar === | ||
== Komputasi == | == Komputasi == | ||
Revision as of 17:17, 13 February 2020
Contents
Cara Manual
Komentar
Pada masalah yang diberikan (persamaan matematika), saya menganalisa persamaan tersebut. Pertama-tama, saya harus selalu memastikan persamaan tersebut dengan cara substitusi langsung. Dalam hal ini, bila substitusi x dengan nilai yang diminta (x=1), maka akan menghasilkan nilai tidak terdefinisi yaitu 0/0.
Hal tersebut berarti nilai x=1 tidak memiliki hasil secara pasti. Bila digambarkan dalam grafik maka dilambangkan dengan lingkaran kosong. Yang berarti nilai tidak terdefinisi. Akan tetapi, kita selalu bisa mencari nilai terdekat dari nilai x=1. Nilai terdekat tersebut bisa saja sebelum atau sesudah x=1. Maka nilai x akan diganti dengan nilai terdekat tersebut. Konsep ini adalah konsep Limit. Dalam hal ini Limit f(x) degan nilai x mendekati 1.