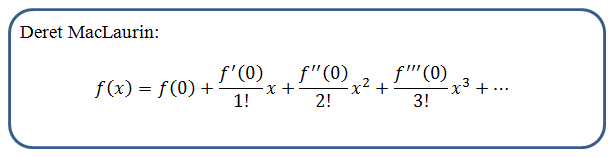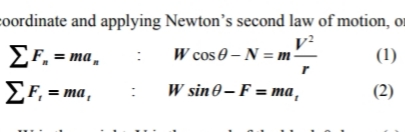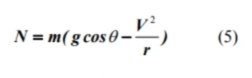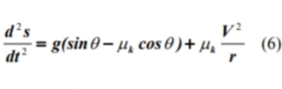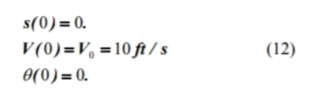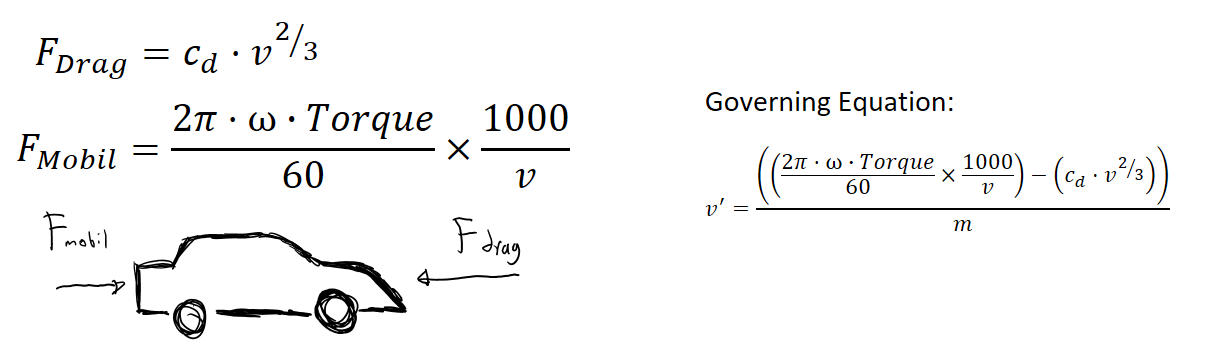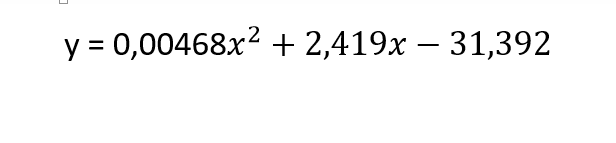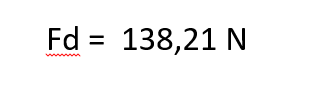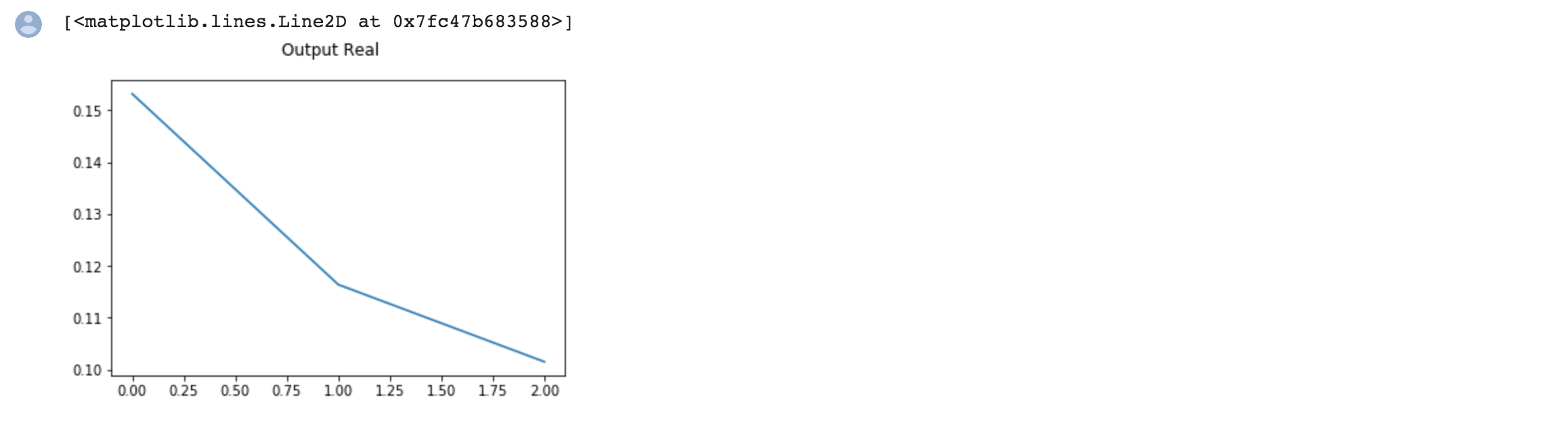Difference between revisions of "Dimas Fahrul Rozi"
| (24 intermediate revisions by the same user not shown) | |||
| Line 119: | Line 119: | ||
Dalam contoh model, kami mengusulkan untuk mengevaluasi posisi, kecepatan dan waktu di mana blok 1 pound meninggalkan permukaan permukaan silinder tempat slide. Blok diasumsikan memiliki kecepatan awal V0 di bagian atas silinder dan tunduk pada gaya gesek kendala koefisien kinetik gesekan, μk (Lihat Gambar 1). Untuk mencapai solusi numerik yang stabil, kami mengasumsikan, tanpa kehilangan keumuman, kecepatan awal spesifik 10 ft / s untuk blok dan mempertimbangkan koefisien gesekan kinetik antara blok dan permukaan menjadi nol dalam satu kasus dan 0,2 dalam lainnya . Jari-jari silinder, r = 5 ft | Dalam contoh model, kami mengusulkan untuk mengevaluasi posisi, kecepatan dan waktu di mana blok 1 pound meninggalkan permukaan permukaan silinder tempat slide. Blok diasumsikan memiliki kecepatan awal V0 di bagian atas silinder dan tunduk pada gaya gesek kendala koefisien kinetik gesekan, μk (Lihat Gambar 1). Untuk mencapai solusi numerik yang stabil, kami mengasumsikan, tanpa kehilangan keumuman, kecepatan awal spesifik 10 ft / s untuk blok dan mempertimbangkan koefisien gesekan kinetik antara blok dan permukaan menjadi nol dalam satu kasus dan 0,2 dalam lainnya . Jari-jari silinder, r = 5 ft | ||
| − | [[File:soal permasalahan. | + | [[File:soal---permasalahan.jpg]] |
Gambar 2 menunjukkan tubuh bebas dan diagram respons inersia dari blok, θ derajat dari atas silinder. | Gambar 2 menunjukkan tubuh bebas dan diagram respons inersia dari blok, θ derajat dari atas silinder. | ||
| − | [[File:gambar 2.jpg]] | + | [[File:gambar---2.jpg]] |
Mengadopsi jalur koordinat dan menerapkan hukum gerak kedua Newton, maka akan memperoleh: | Mengadopsi jalur koordinat dan menerapkan hukum gerak kedua Newton, maka akan memperoleh: | ||
| − | [[File:gambar 3.jpg]] | + | [[File:gambar---3.jpg]] |
Di mana m adalah massa, W adalah bobot, V adalah kecepatan blok θ derajat dari atas, r adalah jari-jari silinder, N adalah gaya normal permukaan, F adalah gaya gesek permukaan dan dan pada adalah komponen normal dan tangensial dari akselerasi blok, masing-masing. Namun: | Di mana m adalah massa, W adalah bobot, V adalah kecepatan blok θ derajat dari atas, r adalah jari-jari silinder, N adalah gaya normal permukaan, F adalah gaya gesek permukaan dan dan pada adalah komponen normal dan tangensial dari akselerasi blok, masing-masing. Namun: | ||
| − | [[File:gambar 4.jpg]] | + | [[File:gambar---4.jpg]] |
Di mana s adalah jalur yang dilalui oleh blok pada permukaan silinder. Memecahkan untuk N dari persamaan (1), akan memperoleh | Di mana s adalah jalur yang dilalui oleh blok pada permukaan silinder. Memecahkan untuk N dari persamaan (1), akan memperoleh | ||
| − | [[File:gambar 5.jpg]] | + | [[File:gambar---5.jpg]] |
subtitusi N dari (5) menjadi (3), dan hasilnya bersama dengan (4) menjadi (2), seseorang mendapat: | subtitusi N dari (5) menjadi (3), dan hasilnya bersama dengan (4) menjadi (2), seseorang mendapat: | ||
| − | [[File:gambar 6.jpg]] | + | [[File:gambar---6.jpg]] |
Kecepatan blok dapat dinyatakan sebagai: | Kecepatan blok dapat dinyatakan sebagai: | ||
| − | [[File:gambar 7.jpg]] | + | [[File:gambar---7.jpg]] |
subtitusi (7) menjadi (6), dan mengatur ulang (8), seseorang tiba pada bentuk persamaan gerak yang mengatur sebagai: | subtitusi (7) menjadi (6), dan mengatur ulang (8), seseorang tiba pada bentuk persamaan gerak yang mengatur sebagai: | ||
| − | [[File:gambar 8.jpg]] | + | [[File:gambar---8.jpg]] |
dan subjek pada kondisi awal | dan subjek pada kondisi awal | ||
| − | [[File:gambar 9.jpg]] | + | [[File:gambar---9.jpg]] |
Masalah yang dihadapi jelas merupakan sistem otonom kebebasan tingkat tunggal (karena s = rθ ) dan, oleh karena itu, harus diatur oleh dua persamaan keadaan orde pertama. Namun, kami merumuskan masalah dengan cara saat ini dengan menggunakan persamaan 9-11 untuk mendapatkan solusi numerik secara terpisah untuk posisi sudut dan lengkung blok. Blok meninggalkan permukaan silinder ketika tidak ada kontak dengannya (N = 0) dan, pada saat yang sama, ketika laju perubahan gaya normal sehubungan dengan θ adalah negatif. Ketika N = 0, persamaan (5) menjadi: | Masalah yang dihadapi jelas merupakan sistem otonom kebebasan tingkat tunggal (karena s = rθ ) dan, oleh karena itu, harus diatur oleh dua persamaan keadaan orde pertama. Namun, kami merumuskan masalah dengan cara saat ini dengan menggunakan persamaan 9-11 untuk mendapatkan solusi numerik secara terpisah untuk posisi sudut dan lengkung blok. Blok meninggalkan permukaan silinder ketika tidak ada kontak dengannya (N = 0) dan, pada saat yang sama, ketika laju perubahan gaya normal sehubungan dengan θ adalah negatif. Ketika N = 0, persamaan (5) menjadi: | ||
| − | [[File:gambar 10.jpg]] | + | [[File:gambar---10.jpg]] |
Dalam pendekatan ini kami memperkirakan variabel dan turunannya dalam persamaan (9), (10), dan (11) sebagai berikut: | Dalam pendekatan ini kami memperkirakan variabel dan turunannya dalam persamaan (9), (10), dan (11) sebagai berikut: | ||
| − | [[File:gambar 11.jpg]] | + | [[File:gambar---11.jpg]] |
Satu juga mendekati kecepatan blok sebagai nilai kecepatan rata-rata pada waktu t dan t + ∆t sebagai: | Satu juga mendekati kecepatan blok sebagai nilai kecepatan rata-rata pada waktu t dan t + ∆t sebagai: | ||
| − | [[File:gambar 12.jpg]] | + | [[File:gambar---12.jpg]] |
Substitusi (14) dan (15) menjadi (9), (10), dan (11), akan memperoleh: | Substitusi (14) dan (15) menjadi (9), (10), dan (11), akan memperoleh: | ||
| − | [[File:gambar 13.jpg]] | + | [[File:gambar---13.jpg]] |
Memecahkan untuk variabel, kecepatan, posisi dan sudut θ pada waktu t dari persamaan (16), sekarang didapat di persamaan diferensial yang mengatur | Memecahkan untuk variabel, kecepatan, posisi dan sudut θ pada waktu t dari persamaan (16), sekarang didapat di persamaan diferensial yang mengatur | ||
| − | [[File:gambar 14.jpg]] | + | [[File:gambar---14.jpg]] |
Untuk memeriksa hasil simulasi, kami mempelajari solusi yang tepat untuk persamaan diferensial yang mengatur gerak untuk kasus tanpa gesekan (μk = 0). Dalam hal itu, mengatur persamaan diferensial gerak berkurang menjadi: | Untuk memeriksa hasil simulasi, kami mempelajari solusi yang tepat untuk persamaan diferensial yang mengatur gerak untuk kasus tanpa gesekan (μk = 0). Dalam hal itu, mengatur persamaan diferensial gerak berkurang menjadi: | ||
| − | [[File:gambar 15.jpg]] | + | [[File:gambar---15.jpg]] |
subjek pada kondisi awal (12) dan kondisi (13). Ini dapat diselesaikan dengan teknik dasar. Menggunakan persamaan (19) dan aturan rantai, persamaan (18) ditulis sebagai | subjek pada kondisi awal (12) dan kondisi (13). Ini dapat diselesaikan dengan teknik dasar. Menggunakan persamaan (19) dan aturan rantai, persamaan (18) ditulis sebagai | ||
| − | [[File:gambar 16.jpg]] | + | [[File:gambar---16.jpg]] |
Setelah substitusi V dari kondisi (13) ke (21) kita sampai pada sudut di mana blok meninggalkan permukaan silinder: | Setelah substitusi V dari kondisi (13) ke (21) kita sampai pada sudut di mana blok meninggalkan permukaan silinder: | ||
| − | |||
Yang pada substitusi dari (22) menjadi (13), kami memperoleh | Yang pada substitusi dari (22) menjadi (13), kami memperoleh | ||
| − | [[File:gambar 18.jpg]] | + | [[File:gambar---18.jpg]] |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''Pseudocode''' | ||
| + | |||
| + | |||
| + | |||
| + | MATLAB Function rkgen to Implement Runge-Kutta Integration Method | ||
| + | |||
| + | % Fourth Order Runge Kutta Method for Solving Simultaneous first order | ||
| + | % Differential Equations | ||
| + | |||
| + | function[tvals,yvals]= rkgen(f,tspan,startval,step) | ||
| + | |||
| + | % Creating Coefficient Vectors | ||
| + | b=[ ];d=[ ]; | ||
| + | b=[1/6 1/3 1/3 1/6]; d =[0 0.5 0.5 1]; | ||
| + | |||
| + | % Indicating the Number of Time Steps and Initial values | ||
| + | steps = (tspan(2) -tspan(1))/step +1; | ||
| + | y=startval; t=tspan(1); | ||
| + | yvals=startval; tvals=tspan(1); | ||
| + | |||
| + | % Calculating k1, k2, k3, and k4 for j=2:steps | ||
| + | k(1,:) = step*feval(f,t,y); | ||
| + | for i=2:4 | ||
| + | if (i==2 | i==3) | ||
| + | cc=0.5; | ||
| + | else | ||
| + | cc=1; | ||
| + | end | ||
| + | k(i,:)= step*feval(f, t+step*d(i),y+(cc*k(i-1,:))'); | ||
| + | |||
| + | end | ||
| + | |||
| + | % Updating Function Values and Time | ||
| + | y1 = y+(b*k)'; | ||
| + | t1=t +step; | ||
| + | tvals=[tvals, t1]; | ||
| + | yvals = [yvals, y1]; | ||
| + | t = t1; y =y1; | ||
| + | end | ||
| + | |||
| + | |||
| + | == Tugas 1 Governing equation == | ||
| + | |||
| + | Berikut ini adalah governing equation dari mobil yang ber gerak | ||
| + | |||
| + | [[File:mobilmobil.png]] | ||
| + | [[File:mobil1mobil.png]] | ||
| + | [[File:mobil2mobil.png]] | ||
| + | |||
| + | '''Pseudocode''' | ||
| + | |||
| + | memasukkan nilai variabel yang diperlukan | ||
| + | |||
| + | g= float(9.8) #gravitational_acceleration | ||
| + | |||
| + | cd=eval(input("drag coefficient: ")) | ||
| + | |||
| + | myu= float(input("koefisien gesek dinamis: ")) | ||
| + | |||
| + | v0=eval(input("initial velocity (m/s): ")) | ||
| + | |||
| + | m=eval(input("mass (kg): ")) | ||
| + | |||
| + | a=eval(input("acceleration (m/s^2): ")) | ||
| + | |||
| + | vt=eval(input("top speed (m/s): ")) | ||
| + | |||
| + | semua dibagi m | ||
| + | |||
| + | fgesek=g*myu | ||
| + | |||
| + | fdrag=(cd*vt**(3/2))/m | ||
| + | |||
| + | ft=a | ||
| + | |||
| + | atot=ft-fdrag-fgesek | ||
| + | |||
| + | t=(vt-v0)/atot | ||
| + | |||
| + | print("waktu mobil untuk mencapai top speed: ",t, "detik") | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Tugas 1 Kelompok== | ||
| + | 1)Abraham theodorus | ||
| + | 2)Dimas fahrul rozi | ||
| + | 3) Muhammad Ichsan | ||
| + | |||
| + | membuat presentasi pengaplikasian top speed dengan python | ||
| + | |||
| + | |||
| + | [[File:dimastugas.mp4]] | ||
| + | |||
| + | '''Pseudocode''' | ||
| + | |||
| + | memasukkan nilai variabel yang diperlukan | ||
| + | |||
| + | g= float(9.8) #gravitational_acceleration | ||
| + | |||
| + | cd=eval(input("drag coefficient: ")) | ||
| + | |||
| + | myu= float(input("koefisien gesek dinamis: ")) | ||
| + | |||
| + | v0=eval(input("initial velocity (m/s): ")) | ||
| + | |||
| + | m=eval(input("mass (kg): ")) | ||
| + | |||
| + | a=eval(input("acceleration (m/s^2): ")) | ||
| + | |||
| + | vt=eval(input("top speed (m/s): ")) | ||
| + | |||
| + | semua dibagi m | ||
| + | |||
| + | fgesek=g*myu | ||
| + | |||
| + | fdrag=(cd*vt**(3/2))/m | ||
| + | |||
| + | ft=a | ||
| + | |||
| + | atot=ft-fdrag-fgesek | ||
| + | |||
| + | t=(vt-v0)/atot | ||
| + | |||
| + | print("waktu mobil untuk mencapai top speed: ",t, "detik") | ||
| + | |||
| + | |||
| + | == Runge Kutta, selasa 5 November 2019 == | ||
| + | |||
| + | Metode Runge-Kutta | ||
| + | Persamaan Diferensial Biasa (PDB) adalah persamaan yang melibatkan satu atau lebih turunan fungsi satu peubah. Solusi dari PDB adalah fungsi tertentu yang memenuhi persamaan tersebut. Berikut beberapa contoh PDB : | ||
| + | Penyelesaian PDB dengan metode deret Taylor tidak praktis karena metode tersebut membutuhkan perhitungan turunan f(x, y). Lagipula, tidak semua fungsi mudah dihitung turunannya, terutama bagi fungsi yang bentuknya rumit. Semakin tinggi orde metode deret Taylor, semakin tinggi turunan fungsi yang harus dihitung. Karena pertimbangan ini, metode deret Taylor yang berorde tinggi pun tidak dapat dapat diterima dalam masalah praktek. | ||
| + | Metode Runge-Kutta adalah alternatif lain dari metode deret Taylor yang tidak membutuhkan perhitungan turunan. Metode ini berusaha mendapatkan derajat ketelitian yang lebih tinggi, dan sekaligus menghindarkan keperluan mencari turunan yang lebih tinggi dengan jalan mengevaluasi fungsi f(x, y) pada titik terpilih dalam setiap selang langkah [CON80]. Metode Runge-Kutta adalah metode PDB yang paling popuper karena banyak dipakai dalam praktek. | ||
| + | |||
| + | [[File:Gov equation.png]] | ||
| + | |||
| + | Bentuk umum metoda Range-Kutta orde-n ialah: | ||
| + | |||
| + | yr+1 = yr + a1k1 + a2k2 + ... + an kn | ||
| + | |||
| + | |||
| + | dengan a1, a2, ..., an adalah tetapan, dan | ||
| + | |||
| + | k1 = hf (xr , yr) | ||
| + | |||
| + | k2 = hf (xr + p1h, yr + q11k1) | ||
| + | |||
| + | k3 = hf (xr + p2h, yr + q21k1 + q22k2) | ||
| + | |||
| + | kn = hf (xr + pn-1h, yr + qn-1,1 k1 + qn-1,2 k2 + ... + qn-1, n-1 kn-1) | ||
| + | |||
| + | Nilai ai, pi, qij dipilih sedemikian rupa sehingga meminimumkan galat per langkah, dan persamaan (P.8.24) akan sama dengan metode deret Taylor dari orde setinggi mungkin. | ||
| + | |||
| + | Galat per langkah metode Runge-Kutta orde-n : O(hn+1) | ||
| + | |||
| + | Galat longgokan metode Runge-Kutta orde-n : O(hn) | ||
| + | |||
| + | Orde metode = n | ||
| + | |||
| + | import math | ||
| + | |||
| + | import cmath | ||
| + | |||
| + | m= float(input("massa mobil: ")) | ||
| + | |||
| + | Cd= float(input("Koefisien Drag Udara: ")) | ||
| + | |||
| + | Myu= float(input("koefisien gesek dinamis: ")) | ||
| + | |||
| + | F = float(input("Engine's Force: ")) | ||
| + | |||
| + | g= float(9.18) #gravitational_acceleration | ||
| + | |||
| + | N = float(m*g) #Normal_Force | ||
| + | |||
| + | V0 = float(0) #inital_speed_value2 | ||
| + | |||
| + | t0 = float(0) #initial time_value | ||
| + | |||
| + | H = 1 #step_size | ||
| + | |||
| + | Error = float(100) | ||
| + | |||
| + | print ("data data runge kutta: ") | ||
| + | |||
| + | def Va(t0, V0): | ||
| + | return ((F)-(Cd*V0**(2/3)-Myu*N)/m) | ||
| + | while(Error>0.0005): | ||
| + | k1 = Va(t0, V0) | ||
| + | k2 = Va(t0 + 0.5, V0 + k1*0.5) | ||
| + | k3 = Va(t0 + 0.5, V0 + k2*0.5) | ||
| + | k4 = Va(t0 + 1, V0 + k3) | ||
| + | V1 = V0 + (1/6)*(k1 + 2*k2 + 3*k3 + k4) | ||
| + | Error = ((V1 - V0) / V1) | ||
| + | V0 = V1 | ||
| + | t1 = t0 + H | ||
| + | t0 = t1 | ||
| + | print (V1) | ||
| + | print ("") | ||
| + | print ("kecepatan max mobil merupakan: ", V1) | ||
| + | print ("waktu ke top speed: ", t0) | ||
| + | == Mencari nilai drag mobil,(selasa, 12 November 2019) == | ||
| + | |||
| + | |||
| + | '''Drag force''' | ||
| + | |||
| + | (Gaya hambat) | ||
| + | |||
| + | Dalam dinamika fluida, gaya hambat (yang kadang-kadang disebut hambatan fluida atau seretan) adalah | ||
| + | gaya yang menghambat pergerakan sebuah benda padat melalui sebuah fluida ( cairan atau gas). | ||
| + | Bentuk gaya hambat yang paling umum tersusun dari sejumlah gaya gesek, | ||
| + | yang bertindak sejajar dengan permukaan benda, plus gaya tekanan, | ||
| + | yang bertindak dalam arah tegak lurus dengan permukaan benda. | ||
| + | Bagi sebuah benda padat yang bergerak melalui sebuah fluida, | ||
| + | gaya hambat merupakan komponen dari aerodinamika gaya resultan atau gaya dinamika fluida | ||
| + | yang bekerja dalam arahnya pergerakan. | ||
| + | Komponen tegak lurus terhadap arah pergerakan ini dianggap sebagai gaya angkat. | ||
| + | Dengan begitu gaya hambat berlawanan dengan arah pergerakan benda, | ||
| + | dan dalam sebuah kendaraan yang digerakkan mesin diatasi dengan gaya dorong. | ||
| + | |||
| + | '''Parameter meshing''' | ||
| + | |||
| + | Parameter meshing yang kami gunakan pada CFDSOF: | ||
| + | |||
| + | [[File:tugastugas11.png]] | ||
| + | |||
| + | '''Check mesh quality''' | ||
| + | |||
| + | [[File:111111tugas.png]] | ||
| + | |||
| + | '''FLuida properties''' | ||
| + | |||
| + | [[File:123tug.png]] | ||
| + | |||
| + | '''Dragforce in paraview''' | ||
| + | |||
| + | kami mengawali pengambilan data kecepatan | ||
| + | dari kecepatan 20m/s hingga 80m/s. | ||
| + | dalam pengambilan data kecepatan | ||
| + | kami melakukan dengan kenaikan 5 m/s | ||
| + | maka akan didapat sebagai berikut: | ||
| + | |||
| + | [[File:tugastugas.png]] | ||
| + | |||
| + | '''Hasil data dan plotting curve''' | ||
| + | |||
| + | Dalam hasil data dan plotting ini | ||
| + | kami menggunakan hubungan drag force dengan kecepatan. | ||
| + | setiap kecepatan mobil akan di plotting | ||
| + | dan dilakukan curve fitting | ||
| + | |||
| + | [[File:curvefittingkel9rev.png]] | ||
| + | |||
| + | hasil curve fitting yang kami lakukan di excel menunjukkan | ||
| + | bahwa kurva antara kecepatan terhadap gaya drag menunjukkan | ||
| + | hubungan berupa persamaan polinominal dalam hal ini merupakan polinimial pangkat 2. | ||
| + | menurut kami hasil curve fitting ini cukup akurat, karena nilai R kuadrat mendekati 1. | ||
| + | |||
| + | karena kkecepatan dan drag force sesuai dengan persamaan berikut maka | ||
| + | |||
| + | [[File:ininiini.png]] | ||
| + | |||
| + | |||
| + | Sehingga | ||
| + | |||
| + | [[File:inini2.png]] | ||
| + | |||
| + | karena kecepatan pada tugas pertama nilai kecepatan = 40 m/s | ||
| + | maka nilai drag forcenya adalah | ||
| + | |||
| + | [[File:edietdoeloeniech.png]] | ||
| + | |||
| + | |||
| + | == Optimasi aerodinamika (selasa, 19 November 2019) == | ||
| + | |||
| + | Prosedur perancangan airfoil dengan menerapkan metode panel telah disusun. Pada prosedur ini geometri airfoil dibangkitkan menggunakan transformasi Joukowski. Dengan transformasi ini bentuk airfoil dapat diperoleh dengan mentransformasikan bentuk lingkaran dengan koordinat titik pusat tertentu. Adapun analisis karakteristik aerodinamikanya dilakukan dengan menggunakan metode panel dimana aliran dianggap bersifat tak viskos (inviscid) dan tak mampat (incompressible). Pada penelitian ini efek viskositas dikaji dengan menerapkan metode interaksi viskos-tak viskos. Untuk keperluan tersebut analisis lapisan batas (boundary layer) dilakukan untuk mendapatkan tebal perpindahan (displacement thickness). Informasi tebal perpindahan ini selanjutnya digunakan untuk update geometri airfoil. Langkah berikutnya adalah optimasi guna mendapatkan geometri airfoil yang mempunya rasio gaya angkat terhadap gaya hambat maksimum yang paling maksimum dengan koordinat titik pusat lingkaran sebagai variabel perancangan. Sebagai pengoptimum (optimizer) digunakan optimasi based gradient methods (fmincon) dan Algoritma Genetika (GA) Dari kedua metode tersebut akan dibandingkan hasilnya pada bilangan Reynold tertentu. Dari hasil yang diperoleh menunjukkan bahwa analisis karakteristik aerodinamika menggunakan metode panel dengan melibatkan interaksi viskos-tak viskos memberikan hasil yang cukup akurat terhadap hasil eksperimen. Sekalipun secara umum hasil optimasi yang diperoleh juga cukup baik akan tetapi memerlukan validasi dan variasi lebih lanjut | ||
| + | |||
| + | |||
| + | == optimasi minimum aerodinamik, (selasa, 26 september 2019) == | ||
| + | |||
| + | '''Airfoil''' | ||
| + | |||
| + | Airfoil merupakan suatu struktur aerodinamika yang banyak digunakan baik pada sayap pesawat | ||
| + | maupun mesin - mesin fluida seperti pompa, kompresor, dan turbin. | ||
| + | Airfoil pada sayap pesawat digunakan untuk mengangkat badan pesawat. | ||
| + | Perbedaan tekanan antara bagian atas dan bawah airfoil menyebabkan pesawat mendapat gaya angkat | ||
| + | |||
| + | |||
| + | '''Airfoil yang diteliti''' | ||
| + | |||
| + | 1. Tipe airfoil yang digunakan adalah airfoil NACA 0012. | ||
| + | 2. Fluida kerja yang digunakan adalah udara yang mengalir secara steady flow, incompressible, viscous, dan uniform pada aliran freestream inlet. | ||
| + | 3. Simulasi dilakukan pada kondisi adiabatik. | ||
| + | 4. Penelitian tidak mengikutsertakan analisa bahan yang diguanakan. | ||
| + | 5. Airfoil merupakan benda tegar yang tidak berdeformasi. | ||
| + | |||
| + | '''Karakteristik airfoil''' | ||
| + | |||
| + | Karakteristik aerodinamika yang meliputi: | ||
| + | a. Total lift coefficient (Cl) | ||
| + | b. Total drag coefficient (Cd) | ||
| + | |||
| + | |||
| + | '''Pembuatan airfoil di Inventor''' | ||
| + | |||
| + | [[File:tugaskuy.png]] | ||
| + | |||
| + | '''Pemindahan airfoil dari inventor ke CFD Sof''' | ||
| + | |||
| + | [[File:tugaskuy1.png]] | ||
| + | |||
| + | '''Proses Meshing pada CFD Sof''' | ||
| + | |||
| + | [[File:tugaskuy2.png]] | ||
| + | |||
| + | '''Penghitungan force drag and force lift di paraview''' | ||
| + | |||
| + | [[File:tugaskuy3.png]] | ||
| + | |||
| + | '''Hasil grafik angle vs gaya drag''' | ||
| + | |||
| + | [[File:tugaskuy4.png]] | ||
| + | |||
| + | '''Hasil grafik angle vs gaya lift''' | ||
| + | |||
| + | [[File:tugaskuy5.png]] | ||
| + | |||
| + | '''grafik angle vs Cd''' | ||
| + | |||
| + | [[File:tugaskuy6.png]] | ||
| + | |||
| + | '''grafik angle vs Cl''' | ||
| + | |||
| + | [[File:tugaskuy7.png]] | ||
| + | |||
| + | |||
| + | '''Optimasi''' | ||
| + | |||
| + | #!/usr/bin/env python | ||
| + | # coding: utf-8 | ||
| + | |||
| + | # In[11]: | ||
| + | |||
| + | |||
| + | import numpy as np | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | |||
| + | def calc_drag(x):#drag | ||
| + | x1 = x[0] | ||
| + | drag = 0.000000001*x1**6-0.0000003*x1**5+0.00003*x1**4-0.0008*x1**3-0.0002*x1**2+0.4312*x1+2.7716 | ||
| + | return drag | ||
| + | |||
| + | def calc_lift(x): #lift | ||
| + | x1 = x[0] | ||
| + | lift = -0.00000001*x1**5-0.000002*x1**4+0.0004*x1**3-0.0147*x1**2+0.0705*x1+5.313 | ||
| + | return lift | ||
| + | |||
| + | def objective(x): #volume yang diminimalkan | ||
| + | return calc_drag(x) | ||
| + | |||
| + | def constraint1(x): #variable SUDUT yang meminimalkan persamaan garis drag | ||
| + | return 90 - calc_drag(x) | ||
| + | def constraint2(x): #variable SUDUT yang meminimalkan persamaan garis lift | ||
| + | return 90 - calc_lift(x) | ||
| + | |||
| + | con1=({'type':'ineq','fun':constraint1}) | ||
| + | con2=({'type':'ineq','fun':constraint2}) | ||
| + | cons = (con1,con2) | ||
| + | |||
| + | x1_guess = 50 | ||
| + | |||
| + | x0 = np.array([x1_guess]) | ||
| + | |||
| + | sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True}) | ||
| + | |||
| + | xopt = sol.x | ||
| + | forceopt = -sol.fun | ||
| + | |||
| + | dragopt = calc_drag(xopt) # drag optimal | ||
| + | liftopt = calc_lift(xopt) # lift optimal | ||
| + | |||
| + | print ('sudut optimal = '+str(-xopt[0])) | ||
| + | print ('total force optimal = '+str(forceopt)) | ||
| + | print ('drag force optimal = '+str(-dragopt)) | ||
| + | print ('lift force optimal = '+str(liftopt)) | ||
| + | |||
| + | |||
| + | # In[10]: | ||
| + | |||
| + | |||
| + | import nump as np | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | |||
| + | def calc_drag(x):#drag | ||
| + | x1 = x[0] | ||
| + | drag = 0.000000001*x1**6-0.0000003*x1**5+0.00003*x1**4-0.0008*x1**3-0.0002*x1**2+0.4312*x1+2.7716 | ||
| + | return drag | ||
| + | |||
| + | def calc_lift(x): #lift | ||
| + | x1 = x[0] | ||
| + | lift = -0.00000001*x1**5-0.000002*x1**4+0.0004*x1**3-0.0147*x1**2+0.0705*x1+5.313 | ||
| + | return lift | ||
| + | |||
| + | def objective(x): #volume yang diminimalkan | ||
| + | return calc_lift(x) | ||
| + | |||
| + | def constraint1(x): #variable SUDUT yang meminimalkan persamaan garis drag | ||
| + | return 90 - calc_drag(x) | ||
| + | def constraint2(x): #variable SUDUT yang meminimalkan persamaan garis lift | ||
| + | return 90 - calc_lift(x) | ||
| + | |||
| + | con1=({'type':'ineq','fun':constraint1}) | ||
| + | con2=({'type':'ineq','fun':constraint2}) | ||
| + | cons = (con1,con2) | ||
| + | |||
| + | x1_guess = 50 | ||
| + | |||
| + | x0 = np.array([x1_guess]) | ||
| + | |||
| + | sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True}) | ||
| + | |||
| + | xopt = sol.x | ||
| + | forceopt = -sol.fun | ||
| + | |||
| + | dragopt = calc_drag(xopt) # drag optimal | ||
| + | liftopt = calc_lift(xopt) # lift optimal | ||
| + | |||
| + | print ('sudut optimal = '+str(xopt[0])) | ||
| + | print ('total force optimal = '+str(-forceopt)) | ||
| + | print ('drag force optimal = '+str(dragopt)) | ||
| + | print ('lift force optimal = '+str(liftopt)) | ||
| + | |||
| + | |||
| + | # In[ ]: | ||
| + | |||
| + | |||
| + | |||
| + | '''Hasil optimasi''' | ||
| + | |||
| + | Hasil optimasi minimum Fd/Fl = -0,29198 | ||
| + | |||
| + | |||
| + | == Neural network(selasa,3 Desember 2019) == | ||
| + | |||
| + | ada pertemuan ini, beberapa kelompok mempresentasikan mengenai optimasi airfoil yang mereka lakukan. Kemudian dijelaskan mengenai neural network yaitu sebuah jaringan neuron yang berfungsi seperti otak manusia, dimana setelah dilatih dapat memprediksi hal-hal. | ||
| + | |||
| + | ANN Adalah sistem pembelajaran terawasi yang dibangun dari sejumlah besar elemen sederhana, yang disebut neuron atau perceptron. Setiap neuron dapat membuat keputusan sederhana, dan memberi makan keputusan itu ke neuron lain, yang diorganisasikan dalam lapisan yang saling berhubungan. | ||
| + | |||
| + | Jika kita tidak menerapkan fungsi Aktivasi maka sinyal output hanya akan menjadi fungsi linier sederhana. Fungsi linier hanyalah polinomial satu derajat. | ||
| + | |||
| + | Contoh dari fungsi Aktivasi, yaitu : | ||
| + | |||
| + | - Sigmoid | ||
| + | |||
| + | - Tanh | ||
| + | |||
| + | - ReLu | ||
| + | |||
| + | - LeakyReLu | ||
| + | |||
| + | - SoftMax | ||
| + | |||
| + | '''Backpropagation''' | ||
| + | Backpropagation adalah algoritma pembelajaran untuk memperkecil tingkat error dengan cara menyesuaikan bobotnya berdasarkan perbedaan output dan target yang diinginkan. Backpropagation juga merupakan sebuah metode sistematik untuk pelatihan multilayer. | ||
| + | |||
| + | Secara umum algoritmanya terdiri dari tiga langkah utama, yaitu : | ||
| + | |||
| + | - Pengambilan input | ||
| + | |||
| + | - Penelusuran error | ||
| + | |||
| + | - Penyesuaian bobot | ||
| + | |||
| + | Langkah pertama untuk membangun ANN: | ||
| + | |||
| + | 1. Mengimport Library yang dibutuhkan | ||
| + | [[File:ANNLIB.png]] | ||
| + | |||
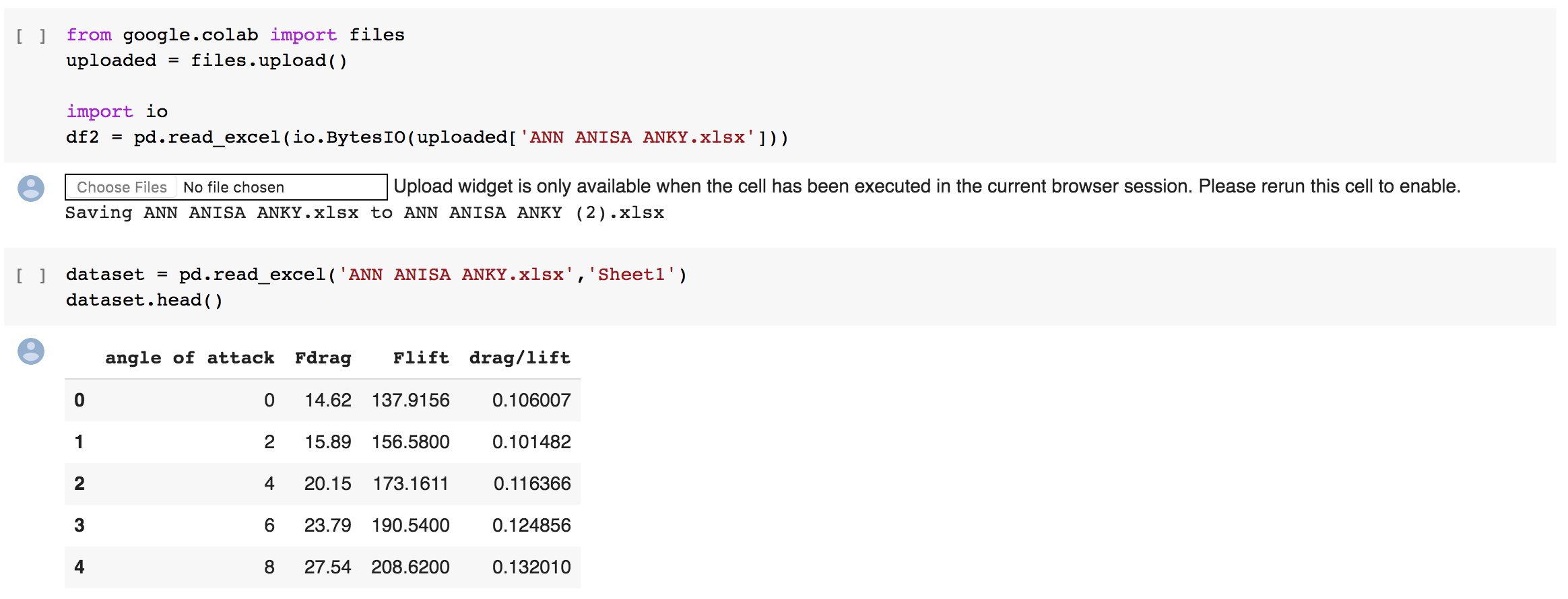
| + | 2. Mengupload file excel yang berisi data drag dan lift airfoil | ||
| + | [[File:Fileexcel1.png]] | ||
| + | [[File:Fileexcel2.png]] | ||
| + | |||
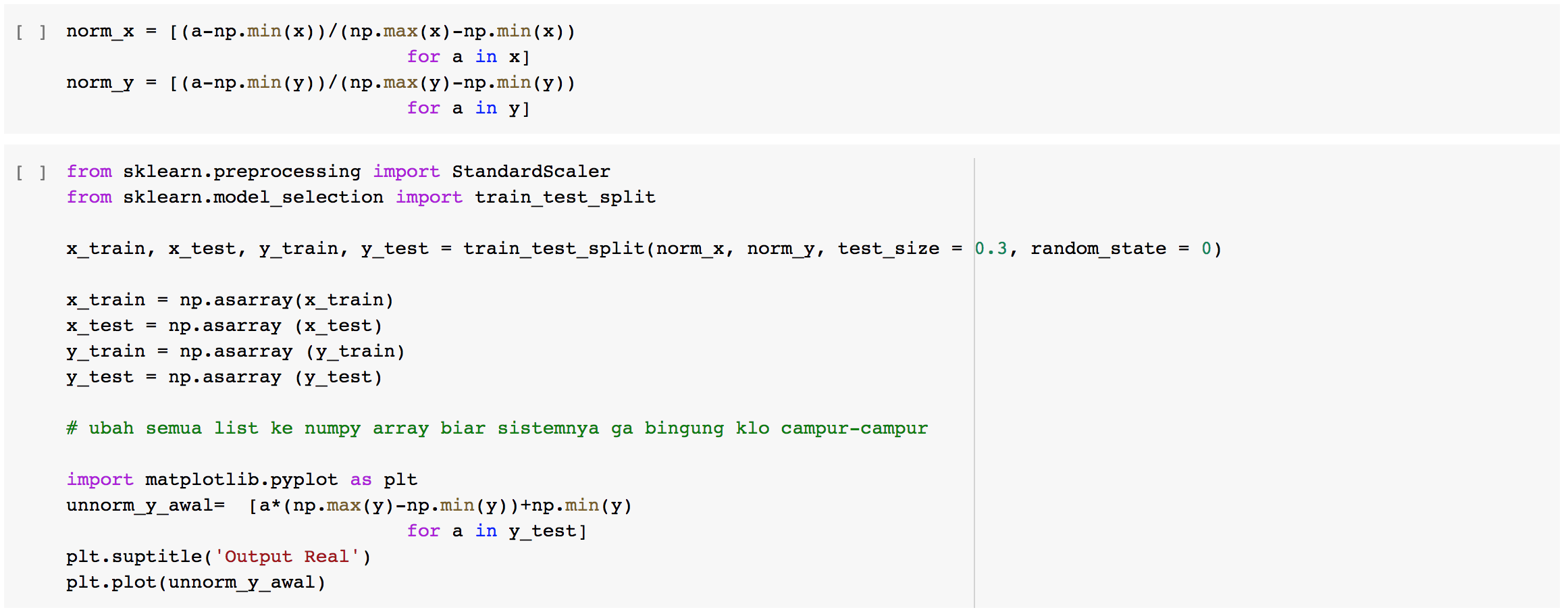
| + | 3. Normalisasi agar matrixnya tidak terlalu besar | ||
| + | [[File:Normalisasi1.png]] | ||
| + | [[File:Normalisasi2.png]] | ||
| + | |||
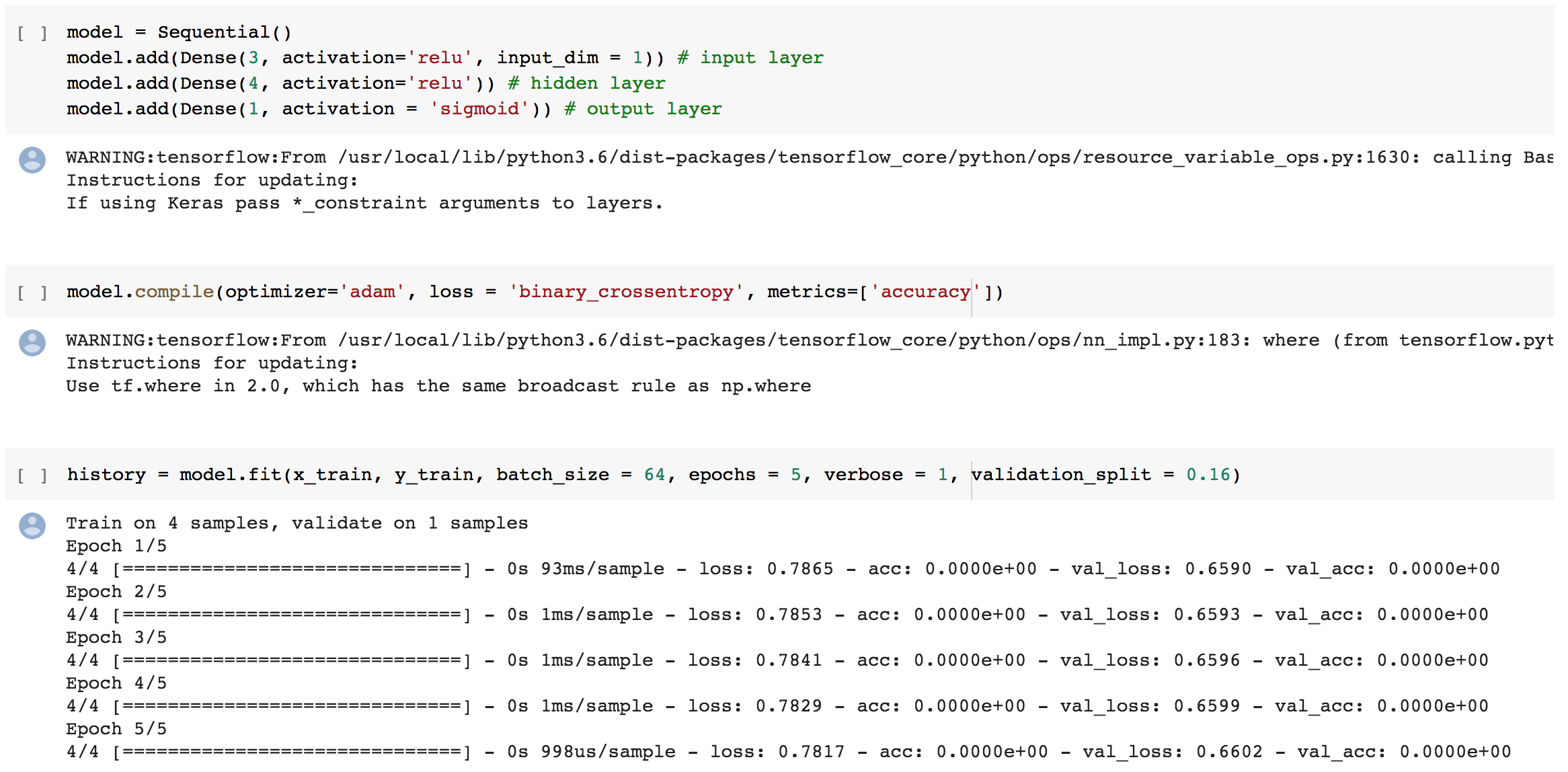
| + | 4. Membuat ANN | ||
| + | [[File:Membuat ann.png]] | ||
| + | |||
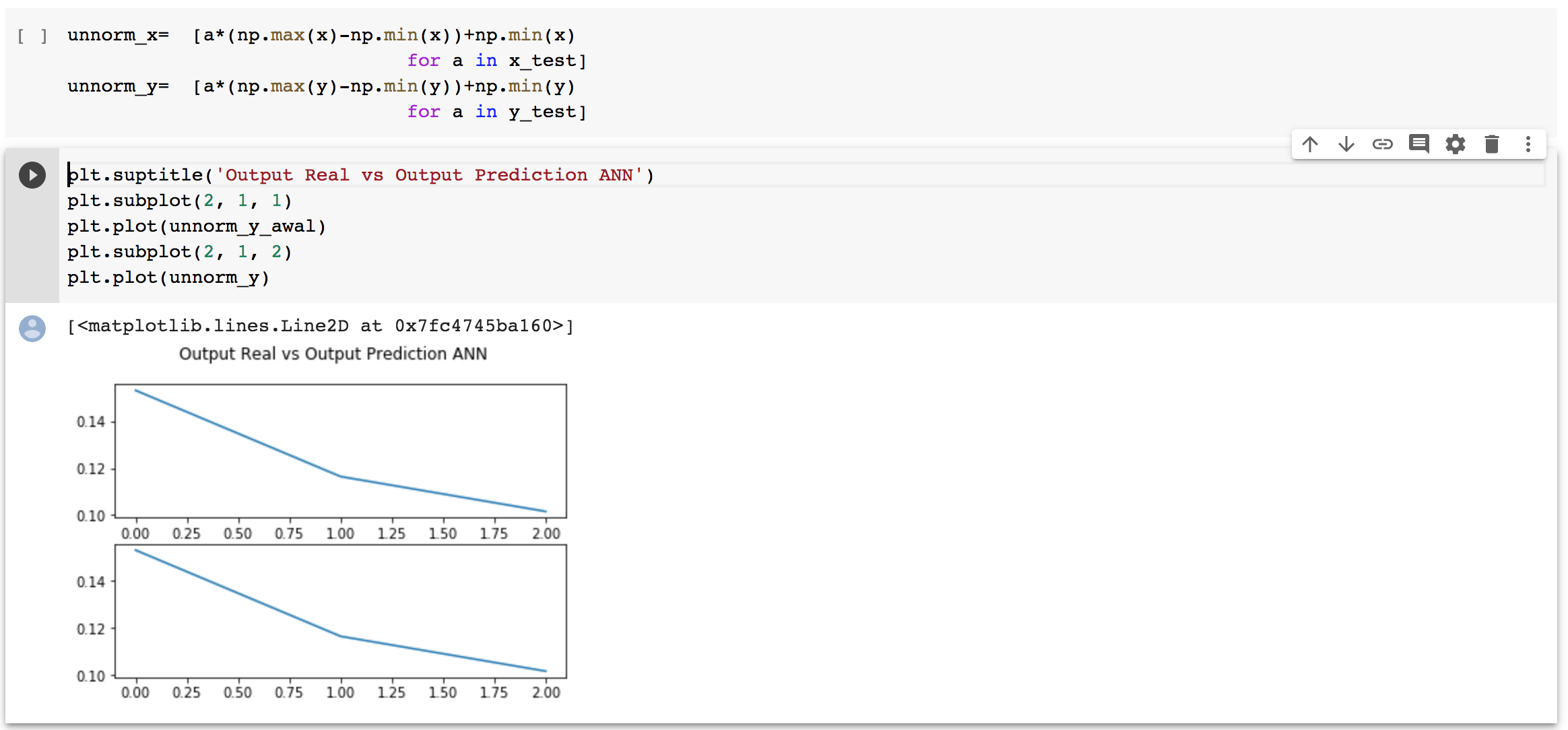
| + | 5. Unnormalize untuk mendapatkan nilai sebenarnya | ||
| + | [[File:Unnormalize.png]] | ||
Latest revision as of 09:20, 30 December 2019
Contents
- 1 Profil
- 2 Selasa, 3 September 2019
- 3 Selasa, 11 September 2019
- 4 selasa,17 September 2019
- 5 selasa,29 Oktober 2019
- 6 Tugas 1
- 7 Tugas 1 Governing equation
- 8 Tugas 1 Kelompok
- 9 Runge Kutta, selasa 5 November 2019
- 10 Mencari nilai drag mobil,(selasa, 12 November 2019)
- 11 Optimasi aerodinamika (selasa, 19 November 2019)
- 12 optimasi minimum aerodinamik, (selasa, 26 september 2019)
- 13 Neural network(selasa,3 Desember 2019)
Profil
Nama : Dimas fahrul rozi
NPM : 1706986340
Program studi : Teknik mesin
Selasa, 3 September 2019
Pertama merupakan penjelassan dari metode numerik Metode Numerik adalah teknik yang digunakan untuk memformulasikan persoalan matematika sehingga dapat dipecahkan dengan operasi perhitungan biasa (+, – , / , *).
Metode Numerik dapat menjadi solusi dalam permasalahan perhitungan matematika yang tidak dapat diselesaikan dengan Metode Analitik. Metode Analitik atau Metode Exact adalah teknik yang digunakan pada sejumlah persoalan yang terbatas dan menghasilkan solusi exact atau solusi sejati.
Dalam peranan Komputer pada Metode Numerik :
Perhitungan dalam metode numerik berupa operasi aritmatika dan dilakukan berulang kali, sehingga dengan adanya komputer dapat mempercepat proses perhitungan tanpa menghasilkan kesalahan. Dengan komputer kita dapat mencoba berbagai kemungkinan solusi yang terjadi akibat perubahan beberapa parameter. Solusi yang diperoleh juga dapat ditingkatkan ketelitiannya dengan mengubah nilai parameter.
Kemudian Deret taylor dan Deret Mclaurin.
Deret taylor Deret Taylor dalam matematika adalah representasi fungsi matematika sebagai jumlahan tak hingga dari suku-suku yang nilainya dihitung dari turunan fungsi tersebut di suatu titik. Deret ini dapat dianggap sebagai limit polinomial Taylor.
Deret Maclaurin
Deret MacLaurin merupakan suatu fungsi f(x) yang memiliki turunan f'(x), f”(x), f”'(x), dan seterusnya yang kontinyu dalam interval I dan a, x I maka untuk x disekitar a yaitu |x – a| < , f(x) dapat diekspansi kedalam Deret Taylor
Dengan menggunakan deret taylor dan deret maclaurin kami mencari nilai x=phi/7
Selasa, 11 September 2019
Di pertemuan kedua kami di ajarkan tentang pseucode
Pengertian Pseudocode
adalah sebuah kode yang digunakan untuk menulis sebuah algoritma dengan cara yang bebas yang tidak terikat dengan bahasa pemrograman tertentu.
Pseudo-code berisikan langkah-langkah untuk menyelesaikan suatu permasalahan [hampir sama dengan algoritma], hanya saja bentuknya sedikit berbeda dari algoritma.
Pseudo-code menggunakan bahasa yang hampir menyerupai bahasa pemrograman. Selain itu biasanya pseudo-code menggunakan bahasa yang mudah dipahami secara universal dan juga lebih ringkas dari pada algoritma.
Pseudo berarti imitasi dan code berarti kode yang dihubungkan dengan instruksi yang ditulis dalam bahasa komputer (kode bahasa pemrograman). Apabila diterjemahkan secara bebas, maka pseudocode berarti tiruan atau imitasi dari kode bahasa pemrograman.
Pada dasarnya, pseudocode merupakan suatu bahasa yang memungkinkan programmer untuk berpikir terhadap permasalahan yang harus dipecahkan tanpa harus memikirkan syntax dari bahasa pemrograman yang tertentu. Tidak ada aturan penulisan syntax di dalam pseudocode. Jadi pseudocode digunakan untuk menggambarkan logika urut-urutan dari program tanpa memandang bagaimana bahasa pemrogramannya. Walaupun pseudocode tidak ada aturan penulisan syntax, di dalam buku ini akan diberikan suatu aturan-aturan penulisan syntax yang cukup sederhana agar pembaca dapat lebih mudah dalam mempelajari algoritma-algoritma yang ada di dalam buku ini. Pseudocode yang ditulis di dalam buku ini akan menyerupai (meniru) syntax-syntax dalam bahasa Pascal. Namun dibuat sesederhana mungkin sehingga tidak akan ada kesulitan bagi pembaca untuk memahami algoritma-algoritma dalam buku ini walaupun pembaca belum pernah mempelajari bahasa Pascal. Contoh algoritma menentukan bilangan terbesar dari tiga bilangan yang ditulis dalam bentuk pseudocode bergaya buku ini.
selasa,17 September 2019
Turunan numerik
Turunan numerik ialah menentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel Dalam melakukan perhitungan turunan metode numerik, intinya kita sangat dianjurkan untuk menggunakan alat hitung baik kalkulator maupun komputer. Kenapa ?, karena kita akan berurusan dengan angka yang memiliki banyak koma. Kemudian kita juga mendapat data-data berupa nilai-nilai suatu titik (nilai x dan y(f(x)). Kemudian kita akan mengidentifikasi metode yang akan kita gunakan berdasarakan data yang ada atau nilai yang akan kita cari.
Metode yang kita gunakan ada 3, yaitu beda maju, beda mundur, dan beda pusat. Tetapi rumus yang digunakan berbeda untuk rumus turunan ke-1 dan ke-2. Perlu diingatkan juga bahwa jarak antar titik yang akan digunakan dalam perhitungan haruslah sama.
Turunan ke-1.
Metode Beda Maju :
Untuk metode beda maju intinya berdasarkan grafik berikut :
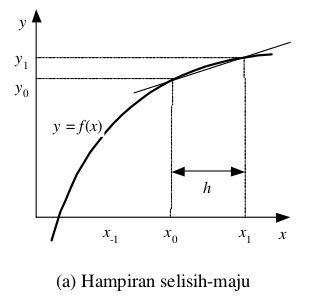 Nah, pada grafik berikut, diibaratkan kita mencari nilai turunan pertama di titik x0 atau f’(x0). Maka kita bisa mencari nilai turunannya dengan rumus berikut :
Nah, pada grafik berikut, diibaratkan kita mencari nilai turunan pertama di titik x0 atau f’(x0). Maka kita bisa mencari nilai turunannya dengan rumus berikut :
f’(x0) = f(x1)-f(x0)/(x1-x0).
Nah, untuk x1-x0 biasanya sering dikenal dengan h (selisih antara dua buah titik terdekat) *aturan h berlaku untuk semua metode.
2. Metode Beda Mundur
Bisa diperhatikan terlebih dahulu grafiknya :
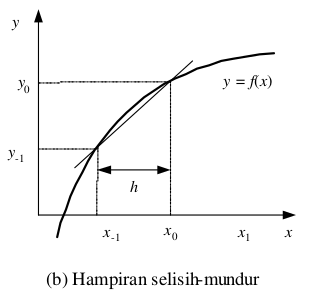 Pada grafik berikut, dengan menggunakan metode beda mundur. Kita bisa mencari nilai dari f’(x0) menggunakan rumus berikut :
Pada grafik berikut, dengan menggunakan metode beda mundur. Kita bisa mencari nilai dari f’(x0) menggunakan rumus berikut :
f’(x0) = f(x0)-f(x-1)/(x0-x-1)
3. Metode beda pusat Bisa diperhatikan terlebih dahulu grafik berikut :
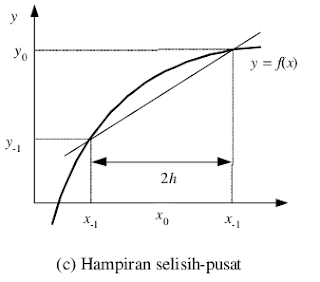 Untuk rumus beda pusat sendiri adalah sebagai berikut :
Untuk rumus beda pusat sendiri adalah sebagai berikut :
f’(x0) = f(x+1)-f(x-1)/(x+1-x-1)
selasa,29 Oktober 2019
Pengenalan phyton IDE
IDE (Integrated Development Environment) adalah program komputer sebagai lingkungan pengembangan aplikasi atau program komputer yang mempunyai beberapa fasilitas yang dibutuhkan dalam pembangunan perangkat lunak (Software).Tujuan dari IDE yaitu untuk menyediakan semua utilitas yang dibutuhkan untuk membangun perangkat lunak. Menjadi seorang programmer diharuskan untuk mengetahui berbagai Integrated Development Environment untuk pembangunan perangkat lunak. Selain itu, IDE merupakan sebuah perangkat lunak aplikasi yang memberikan fasilitas kepada programmer komputer pada saat membuat program. Biasanya IDE terdiri dari source code editor build automation tools dan debugger sebuah IDE, atau secara umum bisa diterjemahkan sebagai Lingkungan Pengembangan Terpadu, setidaknya memiliki fasilitas seperti :
1)Editor, fasilitas ini diperuntukan menuliskan kode atau fungsi-fungsi yang bisa diterjemahkan oleh mesin komputer sebagai kode programming. 2)Compiler, Berfungsi untuk menjalankan bentuk kode program yang di tuliskan di Editor dan mengubah dalam bentuk binary yang selanjutnya akan ditampilkan sesuai perintah-perintah kode mesin. 3)Debuger, Berguna untuk mengecek dan juga mengetes jalannya kode program untuk mencari atau mendebug kesalahan dari program. 4)Frame/Views, fasilitias yang satu ini berguna untuk menujukan atau menampilkan hasil dari perintah-perintah kode program yang dieksekusikan oleh Compiler dari Editor. Terdapat beberapa IDE yang saat ini populer dan sangat mendukung developer dalam mengembangkan perangkat lunak (Software) untuk beberapa platform (iOs Apps, Desktop Apps, Web Apps dan Android Apps,).
Tugas 1
Contoh permasalahan Dalam contoh model, kami mengusulkan untuk mengevaluasi posisi, kecepatan dan waktu di mana blok 1 pound meninggalkan permukaan permukaan silinder tempat slide. Blok diasumsikan memiliki kecepatan awal V0 di bagian atas silinder dan tunduk pada gaya gesek kendala koefisien kinetik gesekan, μk (Lihat Gambar 1). Untuk mencapai solusi numerik yang stabil, kami mengasumsikan, tanpa kehilangan keumuman, kecepatan awal spesifik 10 ft / s untuk blok dan mempertimbangkan koefisien gesekan kinetik antara blok dan permukaan menjadi nol dalam satu kasus dan 0,2 dalam lainnya . Jari-jari silinder, r = 5 ft
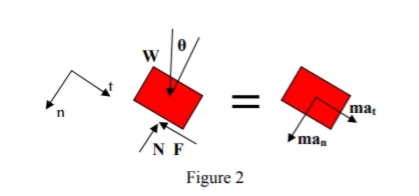
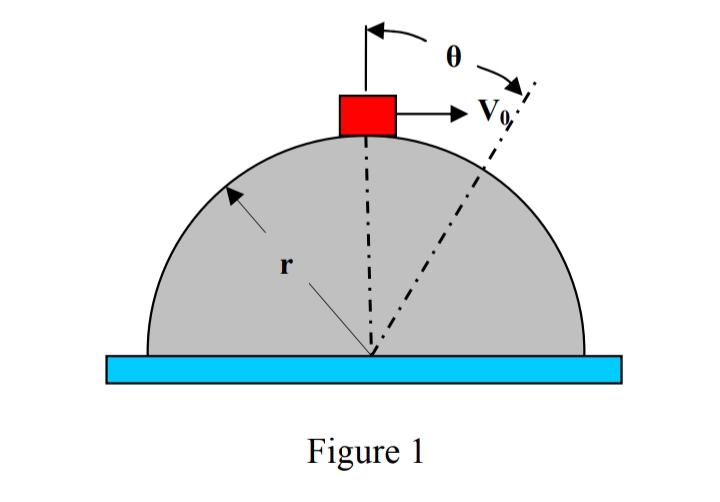 Gambar 2 menunjukkan tubuh bebas dan diagram respons inersia dari blok, θ derajat dari atas silinder.
Gambar 2 menunjukkan tubuh bebas dan diagram respons inersia dari blok, θ derajat dari atas silinder.
Mengadopsi jalur koordinat dan menerapkan hukum gerak kedua Newton, maka akan memperoleh:
Di mana m adalah massa, W adalah bobot, V adalah kecepatan blok θ derajat dari atas, r adalah jari-jari silinder, N adalah gaya normal permukaan, F adalah gaya gesek permukaan dan dan pada adalah komponen normal dan tangensial dari akselerasi blok, masing-masing. Namun:
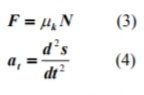 Di mana s adalah jalur yang dilalui oleh blok pada permukaan silinder. Memecahkan untuk N dari persamaan (1), akan memperoleh
Di mana s adalah jalur yang dilalui oleh blok pada permukaan silinder. Memecahkan untuk N dari persamaan (1), akan memperoleh
subtitusi N dari (5) menjadi (3), dan hasilnya bersama dengan (4) menjadi (2), seseorang mendapat:
Kecepatan blok dapat dinyatakan sebagai:
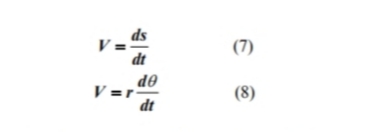
subtitusi (7) menjadi (6), dan mengatur ulang (8), seseorang tiba pada bentuk persamaan gerak yang mengatur sebagai:
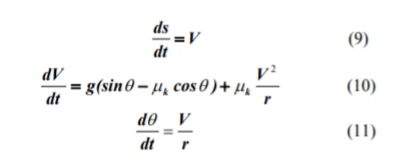
Masalah yang dihadapi jelas merupakan sistem otonom kebebasan tingkat tunggal (karena s = rθ ) dan, oleh karena itu, harus diatur oleh dua persamaan keadaan orde pertama. Namun, kami merumuskan masalah dengan cara saat ini dengan menggunakan persamaan 9-11 untuk mendapatkan solusi numerik secara terpisah untuk posisi sudut dan lengkung blok. Blok meninggalkan permukaan silinder ketika tidak ada kontak dengannya (N = 0) dan, pada saat yang sama, ketika laju perubahan gaya normal sehubungan dengan θ adalah negatif. Ketika N = 0, persamaan (5) menjadi:
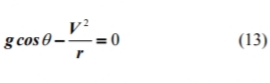
Dalam pendekatan ini kami memperkirakan variabel dan turunannya dalam persamaan (9), (10), dan (11) sebagai berikut:
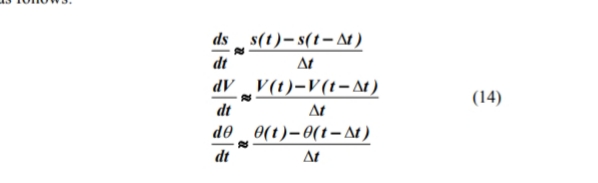
Satu juga mendekati kecepatan blok sebagai nilai kecepatan rata-rata pada waktu t dan t + ∆t sebagai:
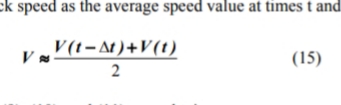
Substitusi (14) dan (15) menjadi (9), (10), dan (11), akan memperoleh:
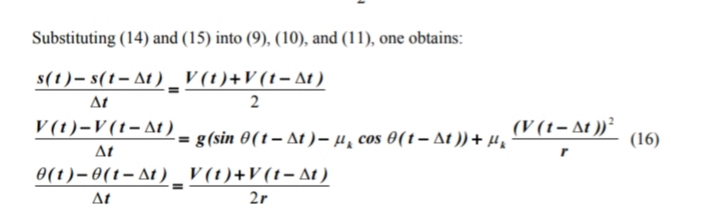
Memecahkan untuk variabel, kecepatan, posisi dan sudut θ pada waktu t dari persamaan (16), sekarang didapat di persamaan diferensial yang mengatur
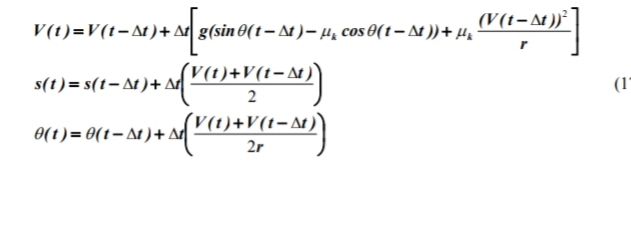
Untuk memeriksa hasil simulasi, kami mempelajari solusi yang tepat untuk persamaan diferensial yang mengatur gerak untuk kasus tanpa gesekan (μk = 0). Dalam hal itu, mengatur persamaan diferensial gerak berkurang menjadi:
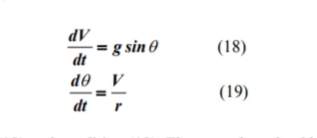
subjek pada kondisi awal (12) dan kondisi (13). Ini dapat diselesaikan dengan teknik dasar. Menggunakan persamaan (19) dan aturan rantai, persamaan (18) ditulis sebagai
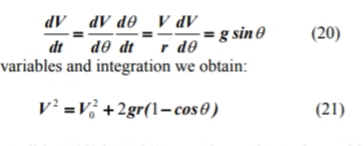
Setelah substitusi V dari kondisi (13) ke (21) kita sampai pada sudut di mana blok meninggalkan permukaan silinder:
Yang pada substitusi dari (22) menjadi (13), kami memperoleh

Pseudocode
MATLAB Function rkgen to Implement Runge-Kutta Integration Method
% Fourth Order Runge Kutta Method for Solving Simultaneous first order % Differential Equations
function[tvals,yvals]= rkgen(f,tspan,startval,step)
% Creating Coefficient Vectors b=[ ];d=[ ]; b=[1/6 1/3 1/3 1/6]; d =[0 0.5 0.5 1];
% Indicating the Number of Time Steps and Initial values steps = (tspan(2) -tspan(1))/step +1; y=startval; t=tspan(1); yvals=startval; tvals=tspan(1);
% Calculating k1, k2, k3, and k4 for j=2:steps k(1,:) = step*feval(f,t,y);
for i=2:4
if (i==2 | i==3)
cc=0.5;
else
cc=1;
end
k(i,:)= step*feval(f, t+step*d(i),y+(cc*k(i-1,:))');
end
% Updating Function Values and Time
y1 = y+(b*k)'; t1=t +step; tvals=[tvals, t1]; yvals = [yvals, y1]; t = t1; y =y1; end
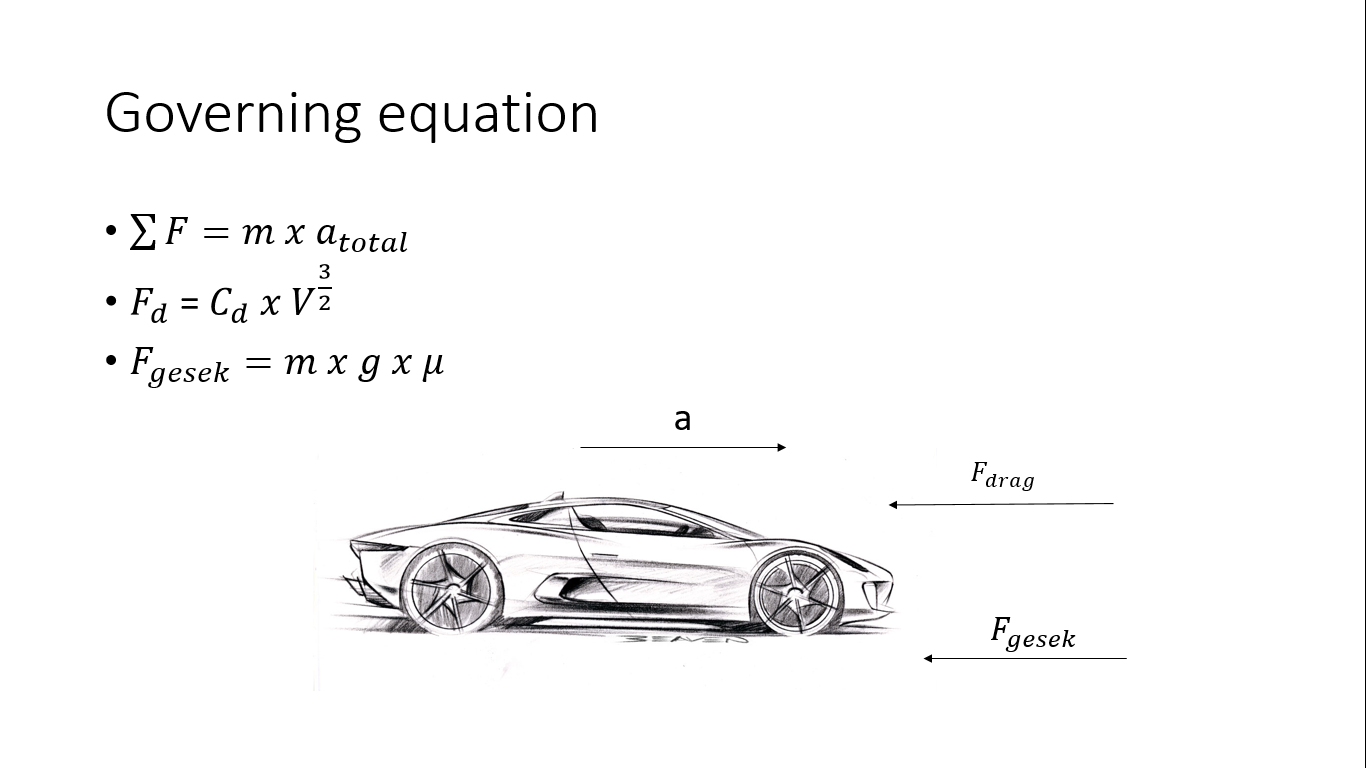
Tugas 1 Governing equation
Berikut ini adalah governing equation dari mobil yang ber gerak
Pseudocode
memasukkan nilai variabel yang diperlukan
g= float(9.8) #gravitational_acceleration
cd=eval(input("drag coefficient: "))
myu= float(input("koefisien gesek dinamis: "))
v0=eval(input("initial velocity (m/s): "))
m=eval(input("mass (kg): "))
a=eval(input("acceleration (m/s^2): "))
vt=eval(input("top speed (m/s): "))
semua dibagi m
fgesek=g*myu
fdrag=(cd*vt**(3/2))/m
ft=a
atot=ft-fdrag-fgesek
t=(vt-v0)/atot
print("waktu mobil untuk mencapai top speed: ",t, "detik")
Tugas 1 Kelompok
1)Abraham theodorus 2)Dimas fahrul rozi 3) Muhammad Ichsan
membuat presentasi pengaplikasian top speed dengan python
Pseudocode
memasukkan nilai variabel yang diperlukan
g= float(9.8) #gravitational_acceleration
cd=eval(input("drag coefficient: "))
myu= float(input("koefisien gesek dinamis: "))
v0=eval(input("initial velocity (m/s): "))
m=eval(input("mass (kg): "))
a=eval(input("acceleration (m/s^2): "))
vt=eval(input("top speed (m/s): "))
semua dibagi m
fgesek=g*myu
fdrag=(cd*vt**(3/2))/m
ft=a
atot=ft-fdrag-fgesek
t=(vt-v0)/atot
print("waktu mobil untuk mencapai top speed: ",t, "detik")
Runge Kutta, selasa 5 November 2019
Metode Runge-Kutta
Persamaan Diferensial Biasa (PDB) adalah persamaan yang melibatkan satu atau lebih turunan fungsi satu peubah. Solusi dari PDB adalah fungsi tertentu yang memenuhi persamaan tersebut. Berikut beberapa contoh PDB : Penyelesaian PDB dengan metode deret Taylor tidak praktis karena metode tersebut membutuhkan perhitungan turunan f(x, y). Lagipula, tidak semua fungsi mudah dihitung turunannya, terutama bagi fungsi yang bentuknya rumit. Semakin tinggi orde metode deret Taylor, semakin tinggi turunan fungsi yang harus dihitung. Karena pertimbangan ini, metode deret Taylor yang berorde tinggi pun tidak dapat dapat diterima dalam masalah praktek. Metode Runge-Kutta adalah alternatif lain dari metode deret Taylor yang tidak membutuhkan perhitungan turunan. Metode ini berusaha mendapatkan derajat ketelitian yang lebih tinggi, dan sekaligus menghindarkan keperluan mencari turunan yang lebih tinggi dengan jalan mengevaluasi fungsi f(x, y) pada titik terpilih dalam setiap selang langkah [CON80]. Metode Runge-Kutta adalah metode PDB yang paling popuper karena banyak dipakai dalam praktek.
Bentuk umum metoda Range-Kutta orde-n ialah:
yr+1 = yr + a1k1 + a2k2 + ... + an kn
dengan a1, a2, ..., an adalah tetapan, dan
k1 = hf (xr , yr)
k2 = hf (xr + p1h, yr + q11k1)
k3 = hf (xr + p2h, yr + q21k1 + q22k2)
kn = hf (xr + pn-1h, yr + qn-1,1 k1 + qn-1,2 k2 + ... + qn-1, n-1 kn-1)
Nilai ai, pi, qij dipilih sedemikian rupa sehingga meminimumkan galat per langkah, dan persamaan (P.8.24) akan sama dengan metode deret Taylor dari orde setinggi mungkin.
Galat per langkah metode Runge-Kutta orde-n : O(hn+1)
Galat longgokan metode Runge-Kutta orde-n : O(hn)
Orde metode = n
import math
import cmath
m= float(input("massa mobil: "))
Cd= float(input("Koefisien Drag Udara: "))
Myu= float(input("koefisien gesek dinamis: "))
F = float(input("Engine's Force: "))
g= float(9.18) #gravitational_acceleration
N = float(m*g) #Normal_Force
V0 = float(0) #inital_speed_value2
t0 = float(0) #initial time_value
H = 1 #step_size
Error = float(100)
print ("data data runge kutta: ")
def Va(t0, V0): return ((F)-(Cd*V0**(2/3)-Myu*N)/m) while(Error>0.0005): k1 = Va(t0, V0) k2 = Va(t0 + 0.5, V0 + k1*0.5) k3 = Va(t0 + 0.5, V0 + k2*0.5) k4 = Va(t0 + 1, V0 + k3) V1 = V0 + (1/6)*(k1 + 2*k2 + 3*k3 + k4) Error = ((V1 - V0) / V1) V0 = V1 t1 = t0 + H t0 = t1 print (V1)
print ("") print ("kecepatan max mobil merupakan: ", V1) print ("waktu ke top speed: ", t0)
Mencari nilai drag mobil,(selasa, 12 November 2019)
Drag force
(Gaya hambat)
Dalam dinamika fluida, gaya hambat (yang kadang-kadang disebut hambatan fluida atau seretan) adalah gaya yang menghambat pergerakan sebuah benda padat melalui sebuah fluida ( cairan atau gas). Bentuk gaya hambat yang paling umum tersusun dari sejumlah gaya gesek, yang bertindak sejajar dengan permukaan benda, plus gaya tekanan, yang bertindak dalam arah tegak lurus dengan permukaan benda. Bagi sebuah benda padat yang bergerak melalui sebuah fluida, gaya hambat merupakan komponen dari aerodinamika gaya resultan atau gaya dinamika fluida yang bekerja dalam arahnya pergerakan. Komponen tegak lurus terhadap arah pergerakan ini dianggap sebagai gaya angkat. Dengan begitu gaya hambat berlawanan dengan arah pergerakan benda, dan dalam sebuah kendaraan yang digerakkan mesin diatasi dengan gaya dorong.
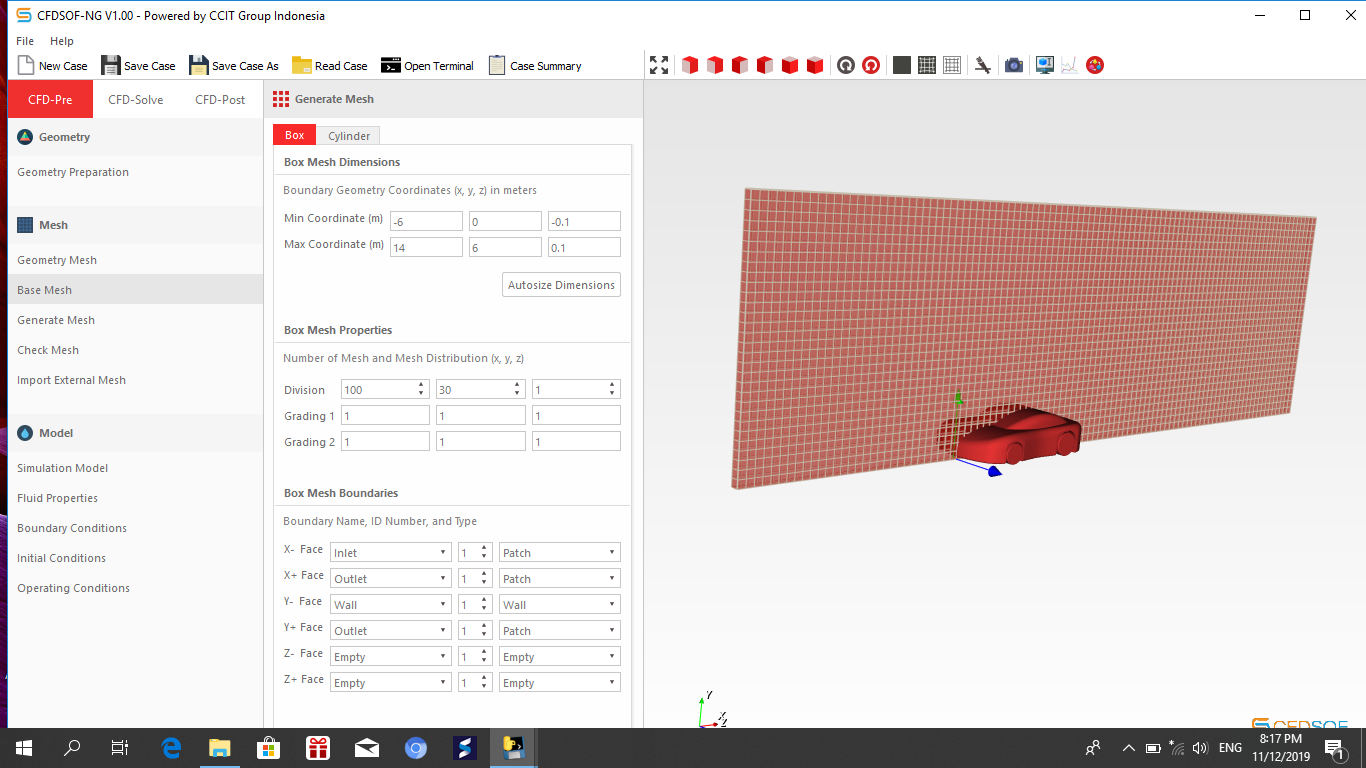
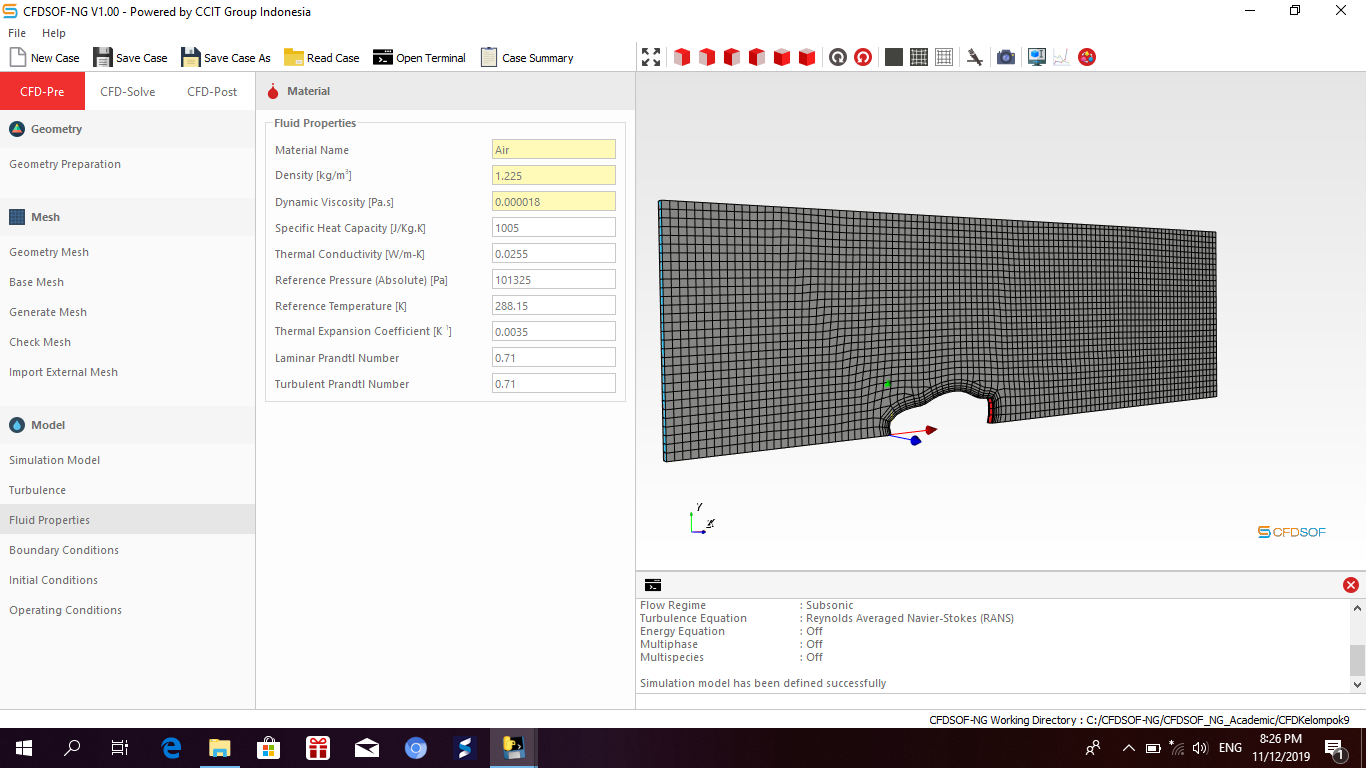
Parameter meshing
Parameter meshing yang kami gunakan pada CFDSOF:
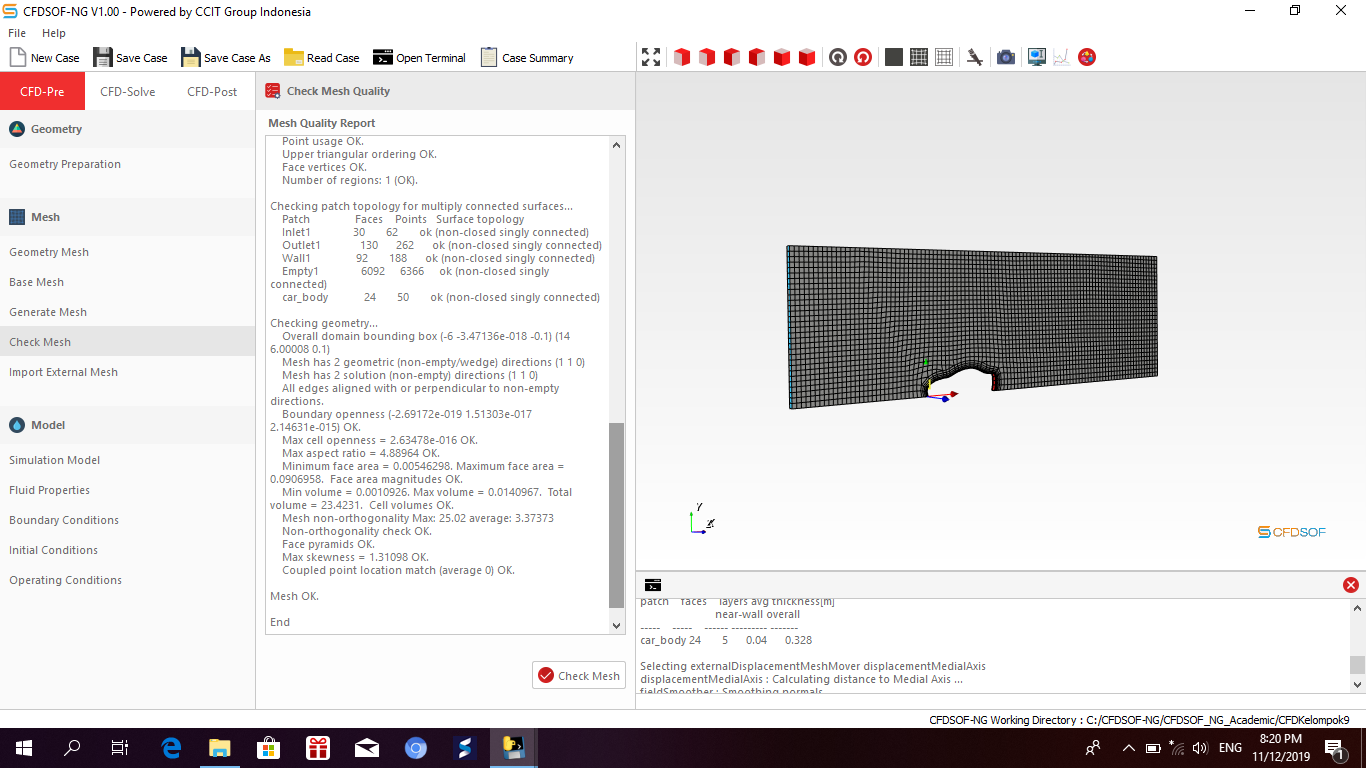
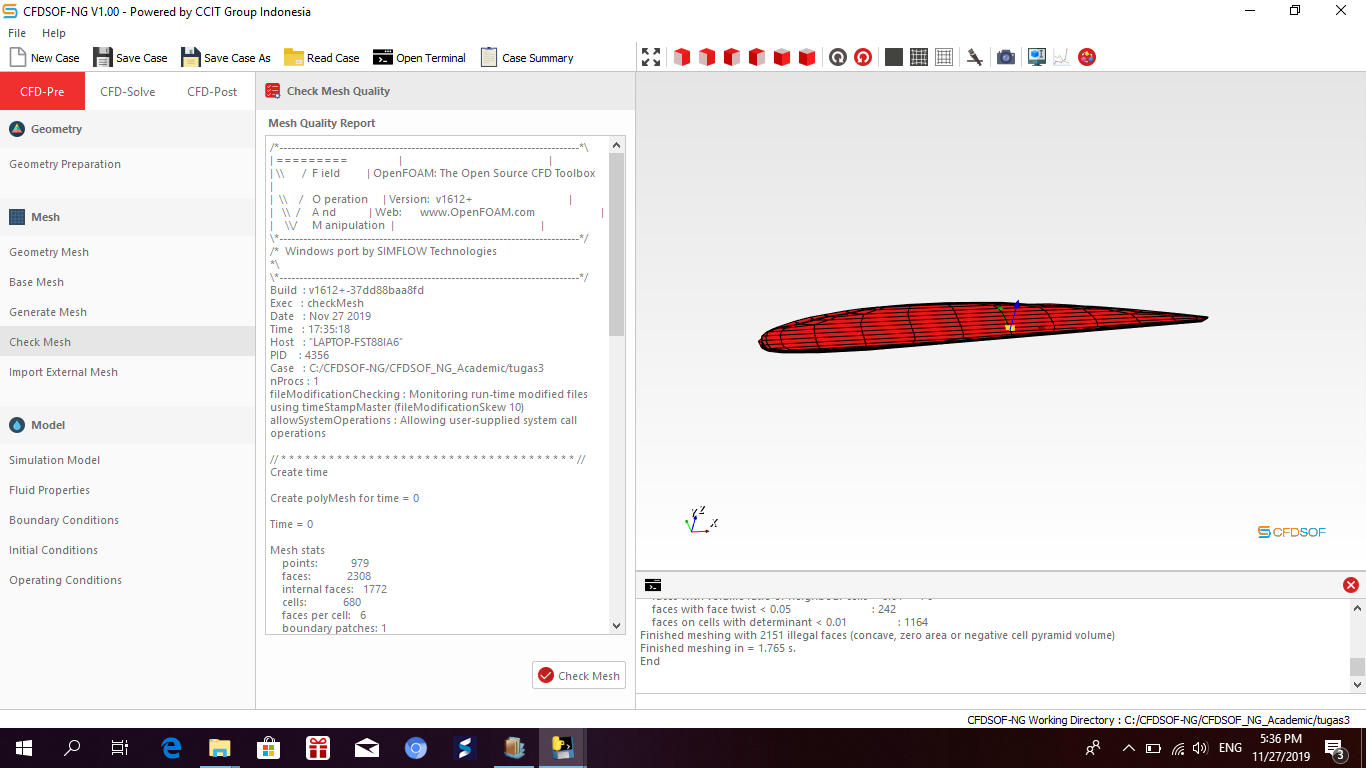
Check mesh quality
FLuida properties
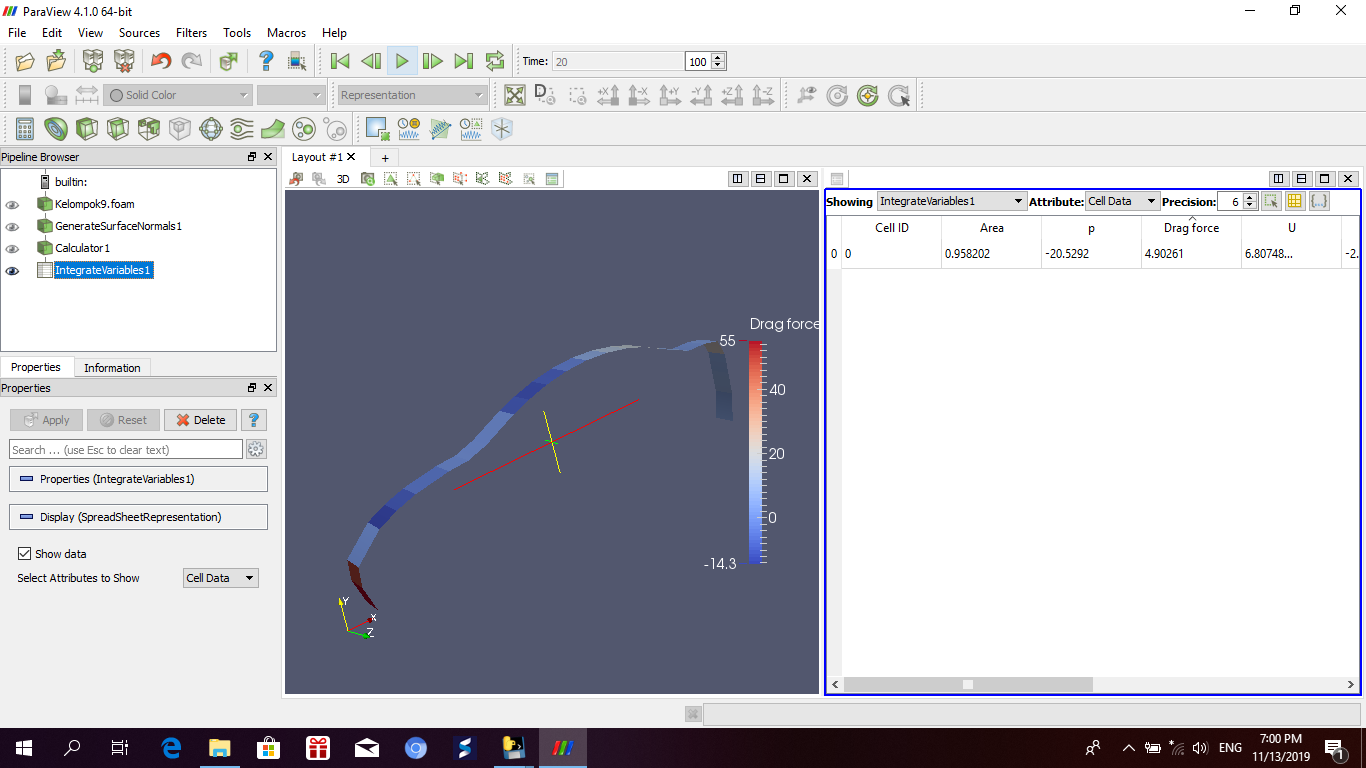
Dragforce in paraview
kami mengawali pengambilan data kecepatan dari kecepatan 20m/s hingga 80m/s. dalam pengambilan data kecepatan kami melakukan dengan kenaikan 5 m/s maka akan didapat sebagai berikut:
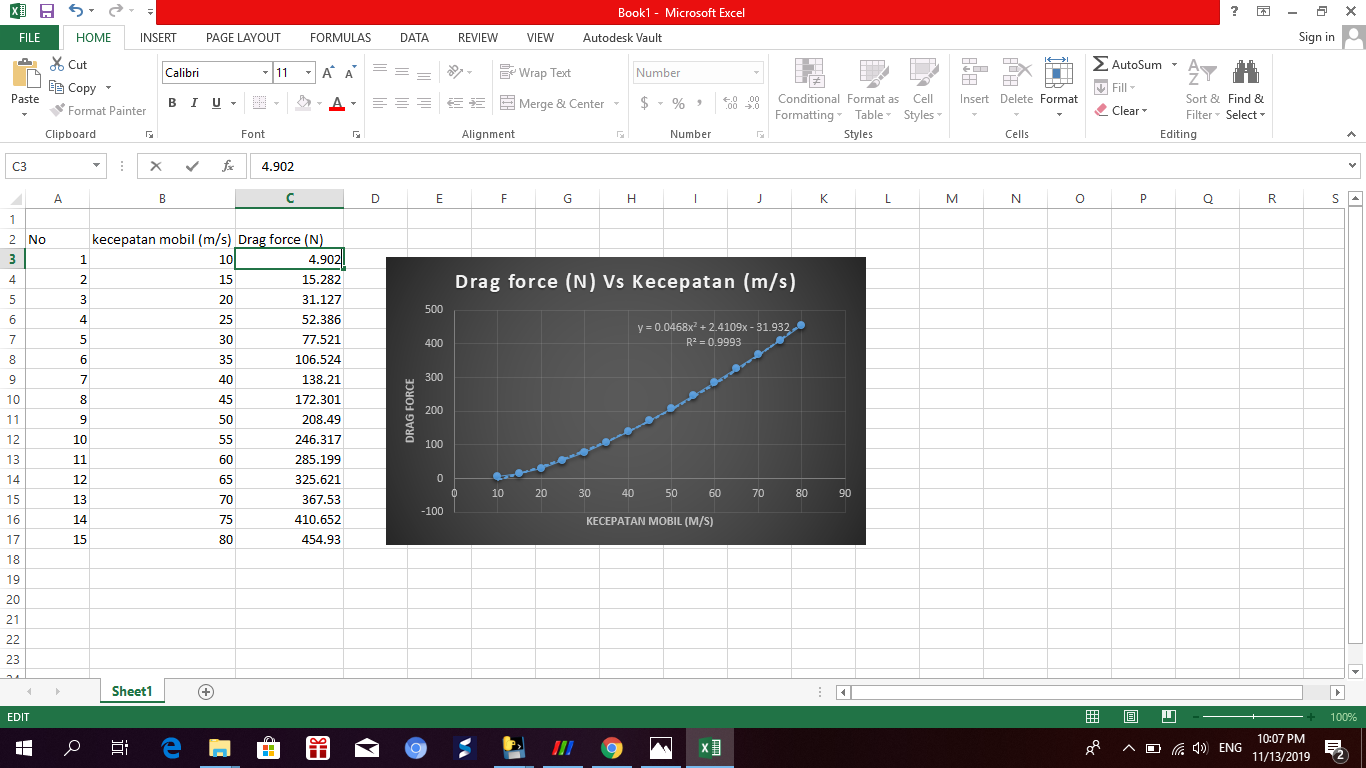
Hasil data dan plotting curve
Dalam hasil data dan plotting ini kami menggunakan hubungan drag force dengan kecepatan. setiap kecepatan mobil akan di plotting dan dilakukan curve fitting
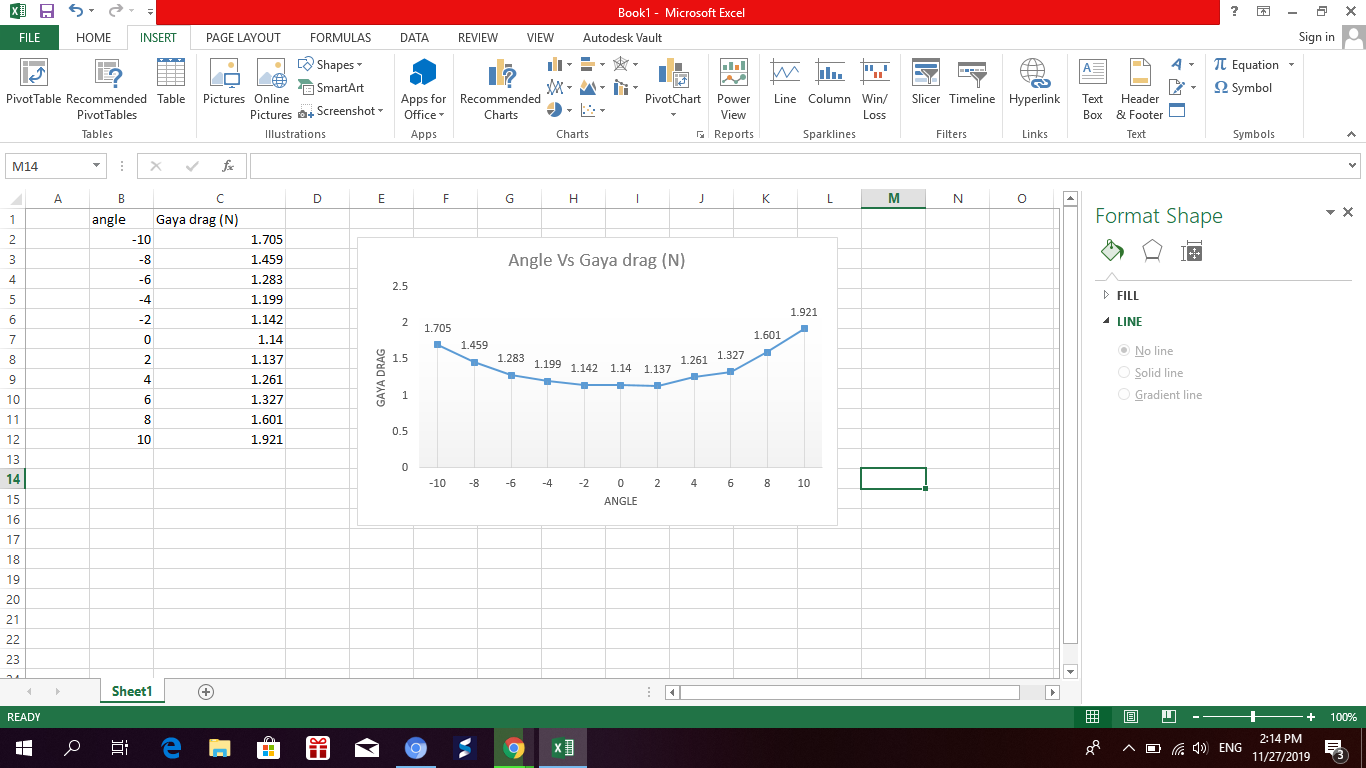
hasil curve fitting yang kami lakukan di excel menunjukkan bahwa kurva antara kecepatan terhadap gaya drag menunjukkan hubungan berupa persamaan polinominal dalam hal ini merupakan polinimial pangkat 2. menurut kami hasil curve fitting ini cukup akurat, karena nilai R kuadrat mendekati 1.
karena kkecepatan dan drag force sesuai dengan persamaan berikut maka
Sehingga
karena kecepatan pada tugas pertama nilai kecepatan = 40 m/s maka nilai drag forcenya adalah
Optimasi aerodinamika (selasa, 19 November 2019)
Prosedur perancangan airfoil dengan menerapkan metode panel telah disusun. Pada prosedur ini geometri airfoil dibangkitkan menggunakan transformasi Joukowski. Dengan transformasi ini bentuk airfoil dapat diperoleh dengan mentransformasikan bentuk lingkaran dengan koordinat titik pusat tertentu. Adapun analisis karakteristik aerodinamikanya dilakukan dengan menggunakan metode panel dimana aliran dianggap bersifat tak viskos (inviscid) dan tak mampat (incompressible). Pada penelitian ini efek viskositas dikaji dengan menerapkan metode interaksi viskos-tak viskos. Untuk keperluan tersebut analisis lapisan batas (boundary layer) dilakukan untuk mendapatkan tebal perpindahan (displacement thickness). Informasi tebal perpindahan ini selanjutnya digunakan untuk update geometri airfoil. Langkah berikutnya adalah optimasi guna mendapatkan geometri airfoil yang mempunya rasio gaya angkat terhadap gaya hambat maksimum yang paling maksimum dengan koordinat titik pusat lingkaran sebagai variabel perancangan. Sebagai pengoptimum (optimizer) digunakan optimasi based gradient methods (fmincon) dan Algoritma Genetika (GA) Dari kedua metode tersebut akan dibandingkan hasilnya pada bilangan Reynold tertentu. Dari hasil yang diperoleh menunjukkan bahwa analisis karakteristik aerodinamika menggunakan metode panel dengan melibatkan interaksi viskos-tak viskos memberikan hasil yang cukup akurat terhadap hasil eksperimen. Sekalipun secara umum hasil optimasi yang diperoleh juga cukup baik akan tetapi memerlukan validasi dan variasi lebih lanjut
optimasi minimum aerodinamik, (selasa, 26 september 2019)
Airfoil
Airfoil merupakan suatu struktur aerodinamika yang banyak digunakan baik pada sayap pesawat maupun mesin - mesin fluida seperti pompa, kompresor, dan turbin. Airfoil pada sayap pesawat digunakan untuk mengangkat badan pesawat. Perbedaan tekanan antara bagian atas dan bawah airfoil menyebabkan pesawat mendapat gaya angkat
Airfoil yang diteliti
1. Tipe airfoil yang digunakan adalah airfoil NACA 0012. 2. Fluida kerja yang digunakan adalah udara yang mengalir secara steady flow, incompressible, viscous, dan uniform pada aliran freestream inlet. 3. Simulasi dilakukan pada kondisi adiabatik. 4. Penelitian tidak mengikutsertakan analisa bahan yang diguanakan. 5. Airfoil merupakan benda tegar yang tidak berdeformasi.
Karakteristik airfoil
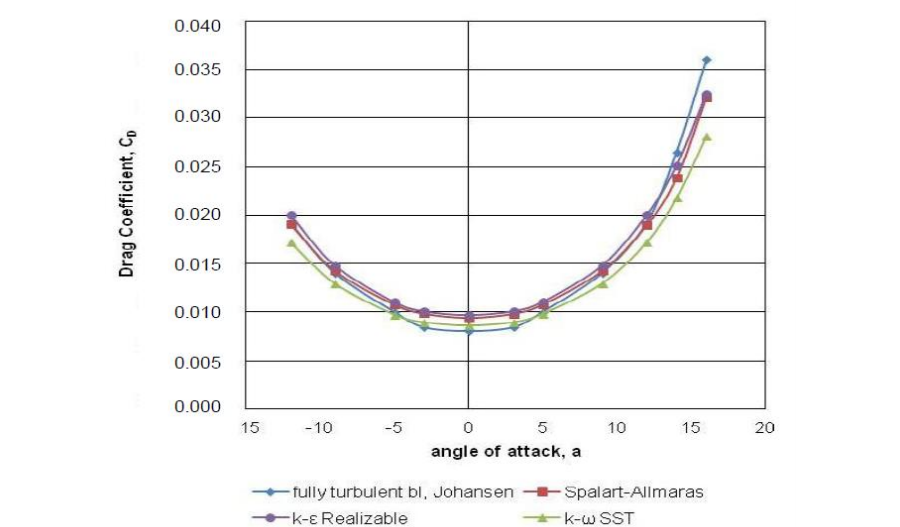
Karakteristik aerodinamika yang meliputi: a. Total lift coefficient (Cl) b. Total drag coefficient (Cd)
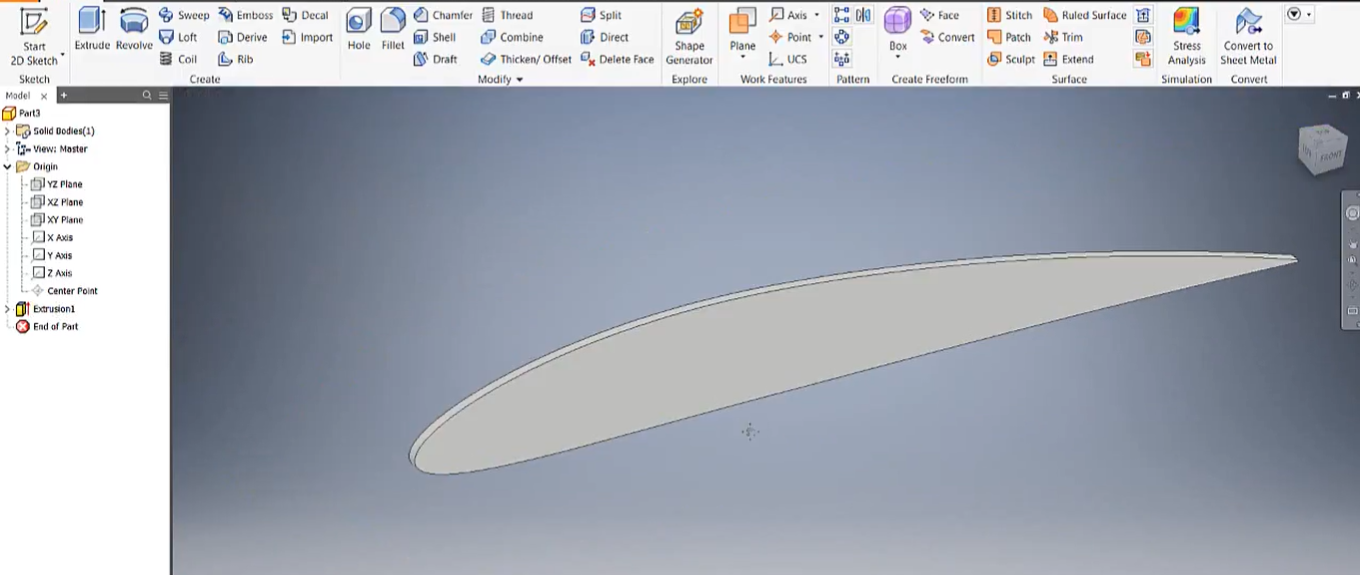
Pembuatan airfoil di Inventor
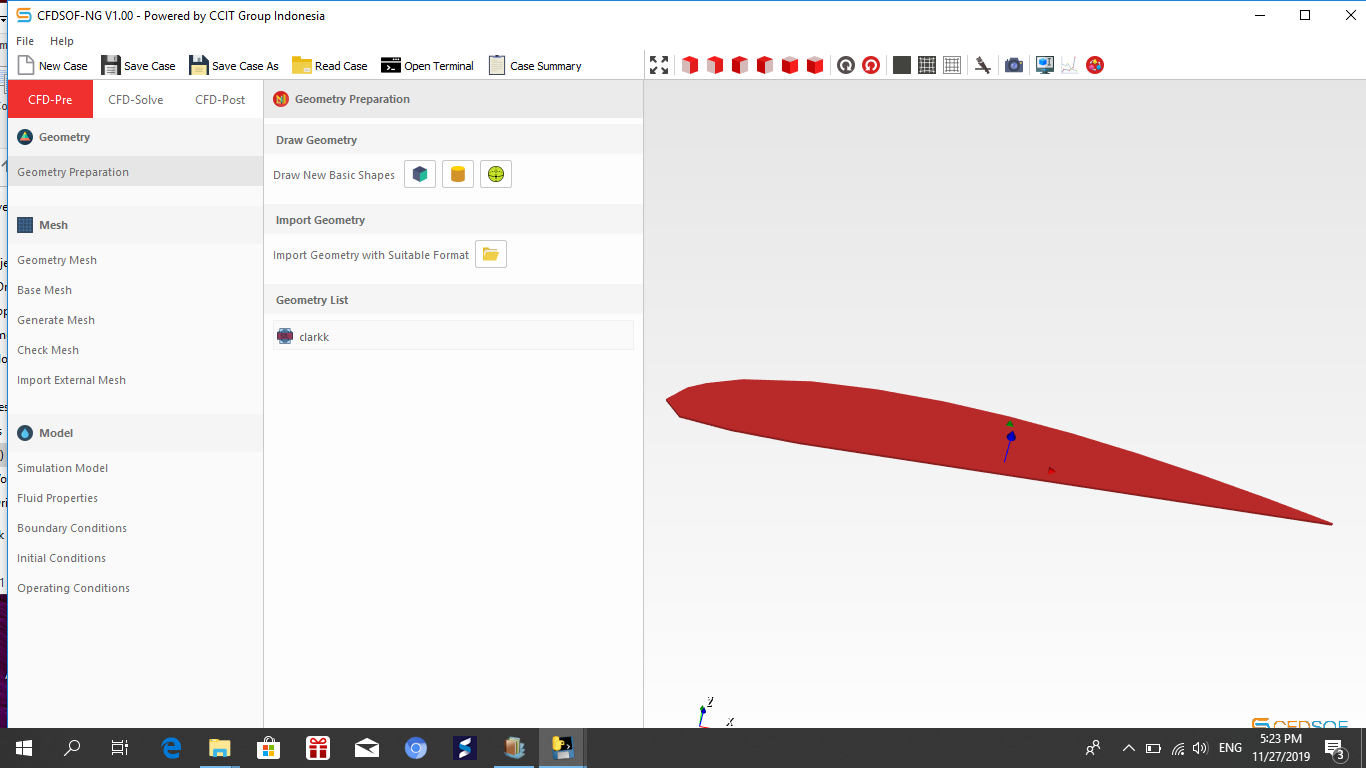
Pemindahan airfoil dari inventor ke CFD Sof
Proses Meshing pada CFD Sof
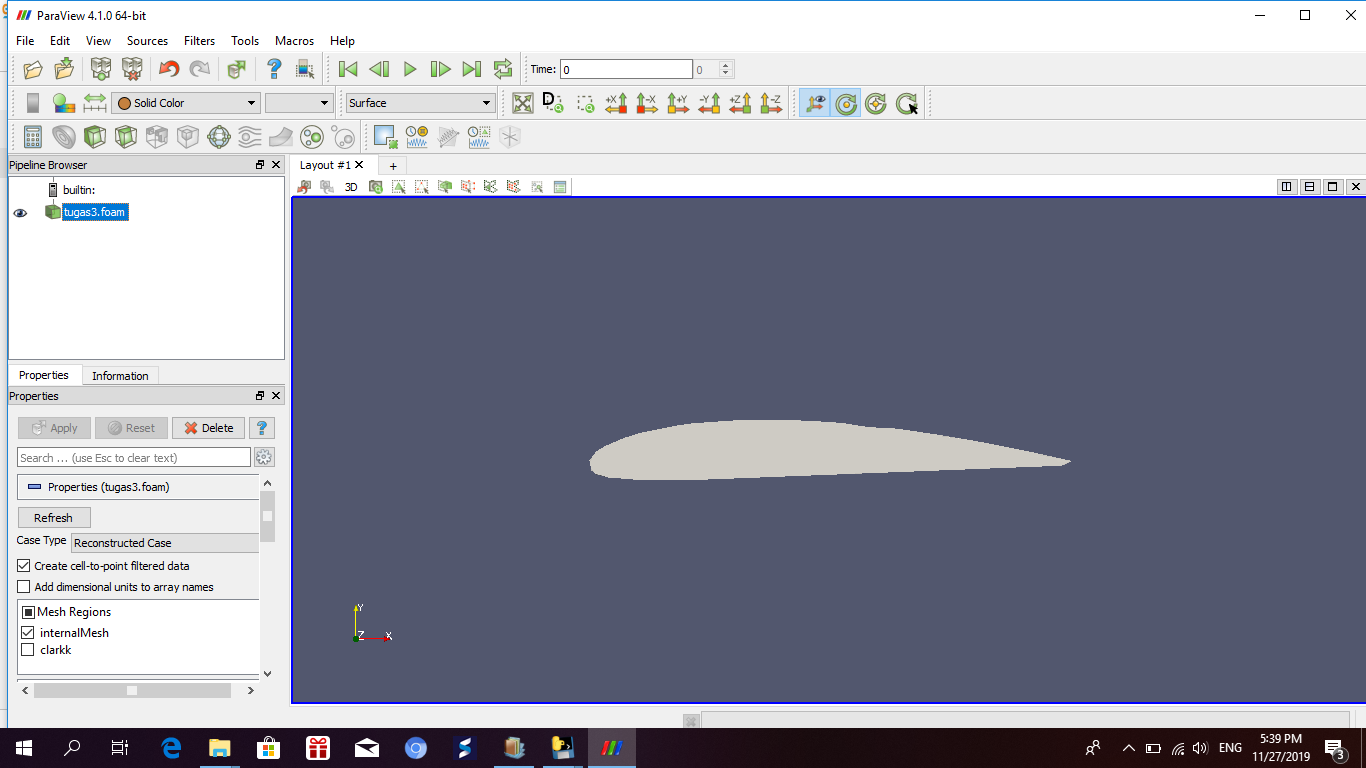
Penghitungan force drag and force lift di paraview
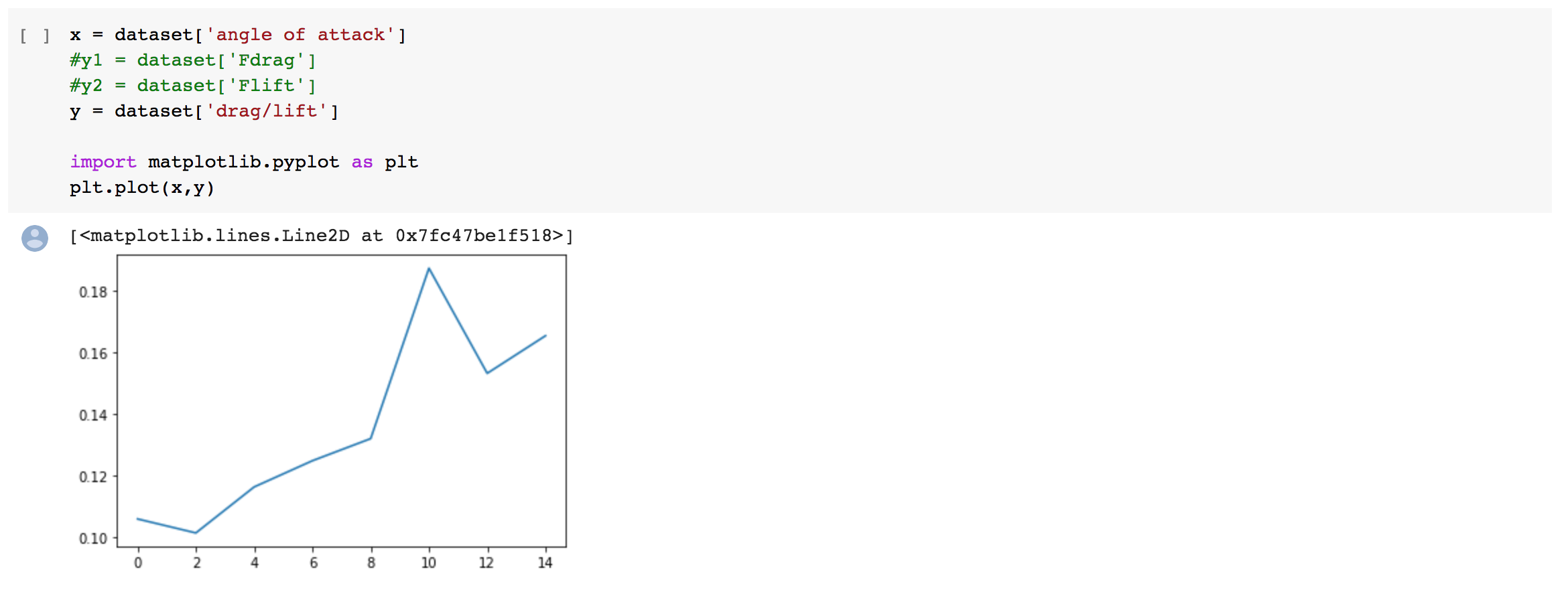
Hasil grafik angle vs gaya drag
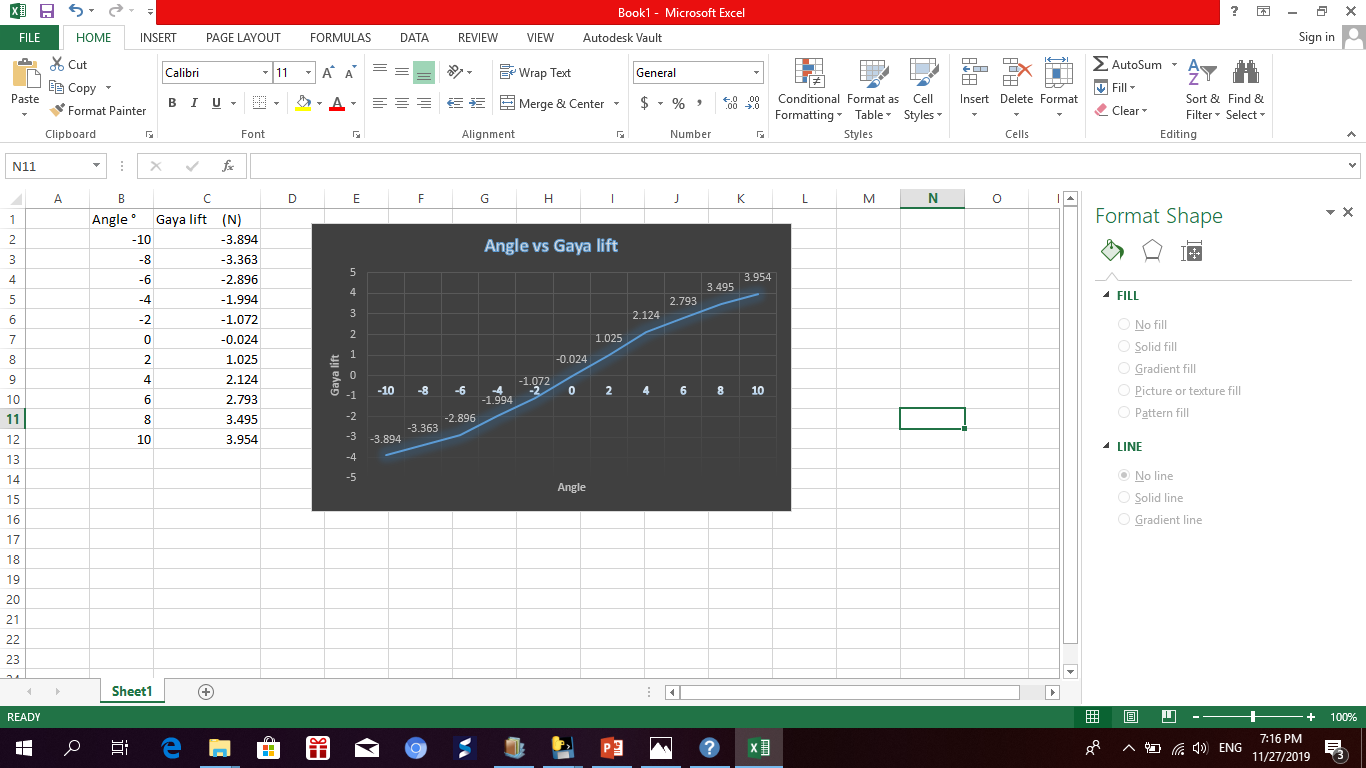
Hasil grafik angle vs gaya lift
grafik angle vs Cd
grafik angle vs Cl
Optimasi
- !/usr/bin/env python
- coding: utf-8
- In[11]:
import numpy as np
from scipy.optimize import minimize
def calc_drag(x):#drag
x1 = x[0] drag = 0.000000001*x1**6-0.0000003*x1**5+0.00003*x1**4-0.0008*x1**3-0.0002*x1**2+0.4312*x1+2.7716 return drag
def calc_lift(x): #lift
x1 = x[0] lift = -0.00000001*x1**5-0.000002*x1**4+0.0004*x1**3-0.0147*x1**2+0.0705*x1+5.313 return lift
def objective(x): #volume yang diminimalkan
return calc_drag(x)
def constraint1(x): #variable SUDUT yang meminimalkan persamaan garis drag
return 90 - calc_drag(x)
def constraint2(x): #variable SUDUT yang meminimalkan persamaan garis lift
return 90 - calc_lift(x)
con1=({'type':'ineq','fun':constraint1}) con2=({'type':'ineq','fun':constraint2}) cons = (con1,con2)
x1_guess = 50
x0 = np.array([x1_guess])
sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True})
xopt = sol.x forceopt = -sol.fun
dragopt = calc_drag(xopt) # drag optimal liftopt = calc_lift(xopt) # lift optimal
print ('sudut optimal = '+str(-xopt[0])) print ('total force optimal = '+str(forceopt)) print ('drag force optimal = '+str(-dragopt)) print ('lift force optimal = '+str(liftopt))
- In[10]:
import nump as np
from scipy.optimize import minimize
def calc_drag(x):#drag
x1 = x[0] drag = 0.000000001*x1**6-0.0000003*x1**5+0.00003*x1**4-0.0008*x1**3-0.0002*x1**2+0.4312*x1+2.7716 return drag
def calc_lift(x): #lift
x1 = x[0] lift = -0.00000001*x1**5-0.000002*x1**4+0.0004*x1**3-0.0147*x1**2+0.0705*x1+5.313 return lift
def objective(x): #volume yang diminimalkan
return calc_lift(x)
def constraint1(x): #variable SUDUT yang meminimalkan persamaan garis drag
return 90 - calc_drag(x)
def constraint2(x): #variable SUDUT yang meminimalkan persamaan garis lift
return 90 - calc_lift(x)
con1=({'type':'ineq','fun':constraint1}) con2=({'type':'ineq','fun':constraint2}) cons = (con1,con2)
x1_guess = 50
x0 = np.array([x1_guess])
sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True})
xopt = sol.x forceopt = -sol.fun
dragopt = calc_drag(xopt) # drag optimal liftopt = calc_lift(xopt) # lift optimal
print ('sudut optimal = '+str(xopt[0])) print ('total force optimal = '+str(-forceopt)) print ('drag force optimal = '+str(dragopt)) print ('lift force optimal = '+str(liftopt))
- In[ ]:
Hasil optimasi
Hasil optimasi minimum Fd/Fl = -0,29198
Neural network(selasa,3 Desember 2019)
ada pertemuan ini, beberapa kelompok mempresentasikan mengenai optimasi airfoil yang mereka lakukan. Kemudian dijelaskan mengenai neural network yaitu sebuah jaringan neuron yang berfungsi seperti otak manusia, dimana setelah dilatih dapat memprediksi hal-hal.
ANN Adalah sistem pembelajaran terawasi yang dibangun dari sejumlah besar elemen sederhana, yang disebut neuron atau perceptron. Setiap neuron dapat membuat keputusan sederhana, dan memberi makan keputusan itu ke neuron lain, yang diorganisasikan dalam lapisan yang saling berhubungan.
Jika kita tidak menerapkan fungsi Aktivasi maka sinyal output hanya akan menjadi fungsi linier sederhana. Fungsi linier hanyalah polinomial satu derajat.
Contoh dari fungsi Aktivasi, yaitu :
- Sigmoid
- Tanh
- ReLu
- LeakyReLu
- SoftMax
Backpropagation Backpropagation adalah algoritma pembelajaran untuk memperkecil tingkat error dengan cara menyesuaikan bobotnya berdasarkan perbedaan output dan target yang diinginkan. Backpropagation juga merupakan sebuah metode sistematik untuk pelatihan multilayer.
Secara umum algoritmanya terdiri dari tiga langkah utama, yaitu :
- Pengambilan input
- Penelusuran error
- Penyesuaian bobot
Langkah pertama untuk membangun ANN:
1. Mengimport Library yang dibutuhkan
2. Mengupload file excel yang berisi data drag dan lift airfoil