Difference between revisions of "Rifky Ramadhan Prakoso"
(Created page with "Nama : Rifky Ramadhan Prakoso NPM : 1706036330 Jurusan : Teknik Mesin") |
|||
| (15 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | Nama : Rifky Ramadhan Prakoso | + | == Profil == |
| + | *Nama : Rifky Ramadhan Prakoso | ||
| + | *NPM : 1706036330 | ||
| + | *Jurusan : Teknik Mesin | ||
| − | + | == Pertemuan Pertama == | |
| + | *Tanggal : 3 September 2019 | ||
| + | *Pengajar : Dr. Ahmad Indra Siswantara dan Dr. Ir. Engkos Achmad Kokasih M.T. | ||
| + | |||
| + | Pada pertemuan pertama kuliah metode numerik, pengajar mengawali perkuliahan dengan memberikan gambaran umum mengenai metode numerik berupa definisi serta pengaplikasiannya di berbagai bidang. Mata kuliah ini merupakan kelanjutan dari mata kuliah yang pernah dipelajari di semester sebelumnya yaitu kalkulus dan aljabar linear sehingga mahasiswa diharapkan untuk sudah menguasai kedua mata kuliah tersebut agar dapat mengikuti mata kuliah metode numerik tanpa kendala. Setelah itu perkuliahan dilanjutkan dengan praktek pengaplikasian metode numerik menggunakan program Microsoft Excel di komputer laboratorium. | ||
| − | + | ||
| + | '''Metode Numerik''' | ||
| + | |||
| + | Metode numerik merupakan suatu teknik untuk menyelesaikan masalah matematika yang efektif dan efisien. Hal ini dapat dicapai karena perhitungan dilakukan oleh pemrograman komputer seperti Microsoft Excel, Phyton maupun Matlab dan bukan dilakukan secara manual menggunakan kalkulator tangan. Implementasi dari metode numerik yang dilengkapi dengan kaidah pemeriksaan konvergensi yang sesuai dalam bahasa pemrograman disebut dengan algoritma numerik. | ||
| + | |||
| + | |||
| + | '''Deret Taylor & Maclaurin''' | ||
| + | |||
| + | Pengajar memberikan pengetahuan bagaimaa cara melakukan perhitungan untul mencari nilai sin(π/7) menggunakan Deret Taylor. | ||
| + | |||
| + | == Pertemuan Kedua == | ||
| + | *Tanggal : 10 September 2019 | ||
| + | *Pengajar : Dr. Ir. Engkos Achmad Kokasih M.T. | ||
| + | |||
| + | Pseudocode adalah sebuah kode yang digunakan untuk menulis sebuah algoritma dengan cara yang bebas yang tidak terikat dengan bahasa pemrograman tertentu. Pseudo berarti imitasi dan code berarti kode yang dihubungkan dengan instruksi yang ditulis dalam bahasa komputer (kode bahasa pemrograman). Apabila diterjemahkan secara bebas, maka pseudocode berarti tiruan atau imitasi dari kode bahasa pemrograman. | ||
| + | |||
| + | Pseudo code sinus | ||
| + | |||
| + | i=1, err=1; suku=x sin=suku while err>1e-7 | ||
| + | |||
| + | ratio=-(x^2)/(2*i)/(2*i+1) | ||
| + | |||
| + | suku=suku*ratio | ||
| + | |||
| + | err=abs(suku/sin) | ||
| + | |||
| + | sin=sin+suku | ||
| + | |||
| + | i=i+1 | ||
| + | |||
| + | |||
| + | Pseudo code kosinus | ||
| + | |||
| + | i=1, err=1; suku=1 cos=suku while err>1e-7 | ||
| + | |||
| + | |||
| + | ratio=-(x^2)/(2*i)/(2*i-1) | ||
| + | |||
| + | suku=suku*ratio | ||
| + | |||
| + | err=abs(suku/cos) | ||
| + | |||
| + | cos=cos+suku | ||
| + | |||
| + | i=i+1 | ||
| + | |||
| + | |||
| + | Pseudo code eksponensial | ||
| + | |||
| + | i=1, err=1; suku=1 exp=suku while err>1e-7 | ||
| + | |||
| + | |||
| + | ratio=(x^2)/i | ||
| + | |||
| + | suku=suku*ratio | ||
| + | |||
| + | err=abs(suku/exp) | ||
| + | |||
| + | exp=exp+suku | ||
| + | |||
| + | i=i+1 | ||
| + | |||
| + | Setelah itu membahas bahasa pemograman. Bahasa Pemrograman merupakan sebuah instruksi untuk memerintah komputer agar bisa menjalankan fungsi tertentu, namun hanya instruksi standar saja.Fungsi dari bahasa pemrograman adalah untuk memerintahkan sebuah komputer agar bisa mengolah data sesuai dengan yang kita inginkan. Jadi, kendali sepenuhnya ada di tangan kita. | ||
| + | |||
| + | Jenis-jenis Bahasa Pemrograman, dimana bahasa pemrograman yang umum diketahui ialah: Pseudo Code, C++, C, Python, PHP, Visual Basic, Java, JavaScript. | ||
| + | |||
| + | == Pertemuan Ketiga == | ||
| + | *Tanggal : 17 September 2019 | ||
| + | *Pengajar : Dr. Ir. Engkos Achmad Kokasih M.T. dan Hanif Furqan | ||
| + | |||
| + | Pada pertemuan ketiga Mata Kuliah Metode Numerik, kami mempelajari tentang Turunan Numerik. Turunan numerik berfungsi untuk mempermudah penurunan suatu persamaan yang rumit. Dalam penggunaannya, turunan numerik dianjurkan untuk dihitung dengan memakai komputer ataupun kalkulator, dikarenakan kompleksnya angka yang dihitung. Untuk menghitung turunan numerik, terdapat tiga pendekatan yang bisa digunakan, yaitu : Turunan maju (Forward), Turunan mundur (Backward), dan Turunan pusat atau tengah (Center). | ||
| + | |||
| + | == Pertemuan Keempat == | ||
| + | *Tanggal : 24 September 2019 | ||
| + | *Pengajar : Dr. Ir. Engkos Achmad Kokasih M.T. | ||
| + | |||
| + | Pada pertemuan kali ini, kami mempelajari root finding algoritma, yang bertujuan untuk mencari sebuah bilangan pembuat nol dari sebuah persamaan atau fungsi. | ||
| + | Pada pertemuan kali ini dicontohkan dengan 3 metode, yaitu Secant, Bisect, dan Newton-Raphson method. | ||
| + | |||
| + | '''Secant method''' adalah metode menggunakan garis secant (gradien garis yang melalui titik (x_0, f(x_0)) dan (x_1, f(x_1))) | ||
| + | |||
| + | '''Bisect method''' adalah metode membagi dua bagian, lalu memilih dari dua bagian ini dipilih bagian mana yang mengandung akar dan bagian yang tidak mengandung akar dibuang. | ||
| + | |||
| + | '''Newton-Raphson method''' adalah metode pencarian akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x) mempunyai turunan. | ||
| + | |||
| + | == Pertemuan Kelima == | ||
| + | *Tanggal : 1 Oktober 2019 | ||
| + | *Pengajar : Dr. Ir. Engkos Achmad Kokasih M.T. | ||
| + | |||
| + | Semua metode numerik memiliki truncation error, baik itu Newton-Raphson, finite element, finite difference dst., dan semua software memiliki truncation error. Untuk memperkecil truncation error, meshing harus dilakukan dengan partisi yang kecil. Apa itu meshing? meshing merupakan pembagian daerah yang dianalisis menjadi partisi-partisi yang sangat kecil, semakin kecil partisi tersebut, semakin akurat hasilnya. Walaupun demikian, hasil yang dihasilkan dari metode numerik tetap diskrit, walaupun terlihat kontinum jika partisinya sangat kecil. Tetapi tidak selalu demikian kasusnya, jika partisi terlalu kecil, maka jumlah iterasi akan semakin banyak, artinya jumlah pengoperasian perhitungan bertambah banyak, dan jumlah rounding akan semakin banyak sehingga rounding error semakin besar. Jadi, untuk menentukan sebesar apa partisinya, ada nilai optimumnya. Untuk mengetahui nilai N (jumlah iterasi) yang paling optimum, nilai iterasi divariasikan dari kecil hingga besar, saat dia sudah tidak berubah banyak maka di titik tersebut lah jumlah iterasinya paling optimum. Begitu juga dengan jumlah mesh perlu divariasikan agar mendapat nilai yang paling optimum. | ||
| + | |||
| + | == Pekerjaan Rumah == | ||
| + | *Tanggal : 29 Oktober 2019 | ||
| + | *Pengajar : Dr. Ahmad Indra Siswantara | ||
| + | |||
| + | Penyelesaian soal menggunakan model Governing equation pada mobil yang memiliki percepatan, gesekan, dan hambatan udara adalah: | ||
| + | |||
| + | F = m*a | ||
| + | |||
| + | F gesek = m*g*cf | ||
| + | |||
| + | F hambat = 0.5*cd*rho*area*vt^2 | ||
| + | |||
| + | |||
| + | Percepatan total didapatkan dengan membagi ketiga gaya tersebut dengan massa | ||
| + | |||
| + | a tot = (F - (F gesek + F hambat))/m | ||
| + | |||
| + | a tot = v(t)/t | ||
| + | |||
| + | t= v(t) / ((F - (F gesek + F hambat))/m) | ||
| + | |||
| + | |||
| + | === Pseudocode === | ||
| + | |||
| + | Berikut adalah pseudocode untuk mencari kecepatan maksimum dan pada waktu berapa. | ||
| + | |||
| + | [[File:Programmobil2.png]] | ||
| + | |||
| + | |||
| + | === Program Python === | ||
| + | |||
| + | Dengan menggunakan metode runge-kutta, berikut adalah program kami dari python | ||
| + | |||
| + | [[File:programmobilrungekutta.png]] | ||
| + | |||
| + | Untuk variable yang digunakan untuk simulasi berupa: | ||
| + | |||
| + | *Power= 500 KW | ||
| + | *Massa= 1500 kg | ||
| + | *Percepatan gravitasi= 9.81 m/s^2 | ||
| + | *Koefisien gesek= 0.7 | ||
| + | *Massa jenis= 1.2 kg/m^2 | ||
| + | *Area= 10 m^2 | ||
| + | *Koefisien drag= 0.2 | ||
| + | |||
| + | === Grafik dan Hasil === | ||
| + | |||
| + | Berikut adalah hasil grafik serta angka kecepatan dan waktu maksimum | ||
| + | |||
| + | [[File:hasilmobil.png]] | ||
| + | |||
| + | == Pertemuan Selasa, 12 November 2019 == | ||
| + | |||
| + | Pada pertemuan ini kami diajarkan cara menggunakan CFDSOF khususnya cara menganalisis suatu fluida yang berjalan pada suatu mobil. Hasil dari simulasi ini kemudian dijadikan tugas kelompok dimana mencari rumus persamaan gaya hambat dari kecepatan. | ||
| + | |||
| + | === Simulasi CFDSOF === | ||
| + | Untuk mendapatkan gaya hambat untuk setiap kecepatan kami melakukan simulasi di CFDSOF. Untuk variabel kecepatannya ditentukan 5 variabel yaitu: | ||
| + | *5 m/s atau 18 km/h untuk rata-rata kecepatan rush hour dalam kota | ||
| + | *20 m/s atau 72 km/h untuk rata-rata kecepatan non-rush hour dalam kota | ||
| + | *30 m/s atau 108 km/h untuk rata-rata kecepatan pada tol | ||
| + | *45 m/s atau 162 km/h untuk kecepatan maksimal mobil biasa | ||
| + | *55 m/s atau 198 km/h untuk kecepatan maksimal mobil sport | ||
| + | |||
| + | Berikut adalah proses simulasi yang kami lakukan dengan aplikasi CFDSOF | ||
| + | |||
| + | [[File:20191216_191216_0015.jpg | 500px ]] | ||
| + | [[File:20191216_191216_0020.jpg | 500px ]] | ||
| + | [[File:20191216_191216_0021.jpg | 500px ]] | ||
| + | [[File:20191216_191216_0022.jpg | 500px ]] | ||
| + | [[File:20191216_191216_0005.jpg | 500px ]] | ||
| + | [[File:20191216_191216_0006.jpg | 500px ]] | ||
| + | |||
| + | === Tabel Hasil Data === | ||
| + | Dari data yang didapatkan dari CFDSOF kami masukkan ke dalam tabel berikut | ||
| + | |||
| + | [[File:tabelcfdsof.png]] | ||
| + | |||
| + | === Plotting Kurva dan Rumus Hambat === | ||
| + | Kemudian kami melakukan plotting kecepatan terhadap gaya hambat menjadi sebuah kurva, berikut adalah hasilnya | ||
| + | |||
| + | |||
| + | [[File:grafikcfdsof.png]] | ||
| + | |||
| + | |||
| + | Dari kurva diatas, didapatkan bahwa rumus untuk gaya drag adalah y = 0,0002x3 + 0,013x2 + 0,7353x - 2,6866 | ||
| + | |||
| + | Dengan y adalah gaya drag dan x adalah kecepetan, sehingga didapatkan rumus akhir Fd = 0,0002v3 + 0,013v2 + 0,7353v - 2,6866 | ||
| + | |||
| + | == Pertemuan Selasa, 26 November 2019 == | ||
| + | |||
| + | Pada pertemuan ini, Pak Ahmad Indra memberikan kuis yang menyangkut pengertian kami mengenai metode numerik. | ||
| + | |||
| + | == Selasa, 3 Desember 2019 == | ||
| + | |||
| + | Pada pertemuan ini, beberapa kelompok mempresentasikan mengenai optimasi airfoil yang mereka lakukan. Kemudian dijelaskan mengenai neural network yaitu sebuah jaringan neuron yang berfungsi seperti otak manusia, dimana setelah dilatih dapat memprediksi hal-hal. | ||
| + | |||
| + | ANN Adalah sistem pembelajaran terawasi yang dibangun dari sejumlah besar elemen sederhana, yang disebut neuron atau perceptron. Setiap neuron dapat membuat keputusan sederhana, dan memberi makan keputusan itu ke neuron lain, yang diorganisasikan dalam lapisan yang saling berhubungan. | ||
| + | |||
| + | Jika kita tidak menerapkan fungsi Aktivasi maka sinyal output hanya akan menjadi fungsi linier sederhana. Fungsi linier hanyalah polinomial satu derajat. | ||
| + | |||
| + | Contoh dari fungsi Aktivasi, yaitu : | ||
| + | |||
| + | - Sigmoid | ||
| + | |||
| + | - Tanh | ||
| + | |||
| + | - ReLu | ||
| + | |||
| + | - LeakyReLu | ||
| + | |||
| + | - SoftMax | ||
| + | |||
| + | Backpropagation adalah algoritma pembelajaran untuk memperkecil tingkat error dengan cara menyesuaikan bobotnya berdasarkan perbedaan output dan target yang diinginkan. Backpropagation juga merupakan sebuah metode sistematik untuk pelatihan multilayer. | ||
| + | |||
| + | Secara umum algoritmanya terdiri dari tiga langkah utama, yaitu : | ||
| + | |||
| + | - Pengambilan input | ||
| + | |||
| + | - Penelusuran error | ||
| + | |||
| + | - Penyesuaian bobot | ||
Latest revision as of 11:18, 24 December 2019
Contents
Profil
- Nama : Rifky Ramadhan Prakoso
- NPM : 1706036330
- Jurusan : Teknik Mesin
Pertemuan Pertama
- Tanggal : 3 September 2019
- Pengajar : Dr. Ahmad Indra Siswantara dan Dr. Ir. Engkos Achmad Kokasih M.T.
Pada pertemuan pertama kuliah metode numerik, pengajar mengawali perkuliahan dengan memberikan gambaran umum mengenai metode numerik berupa definisi serta pengaplikasiannya di berbagai bidang. Mata kuliah ini merupakan kelanjutan dari mata kuliah yang pernah dipelajari di semester sebelumnya yaitu kalkulus dan aljabar linear sehingga mahasiswa diharapkan untuk sudah menguasai kedua mata kuliah tersebut agar dapat mengikuti mata kuliah metode numerik tanpa kendala. Setelah itu perkuliahan dilanjutkan dengan praktek pengaplikasian metode numerik menggunakan program Microsoft Excel di komputer laboratorium.
Metode Numerik
Metode numerik merupakan suatu teknik untuk menyelesaikan masalah matematika yang efektif dan efisien. Hal ini dapat dicapai karena perhitungan dilakukan oleh pemrograman komputer seperti Microsoft Excel, Phyton maupun Matlab dan bukan dilakukan secara manual menggunakan kalkulator tangan. Implementasi dari metode numerik yang dilengkapi dengan kaidah pemeriksaan konvergensi yang sesuai dalam bahasa pemrograman disebut dengan algoritma numerik.
Deret Taylor & Maclaurin
Pengajar memberikan pengetahuan bagaimaa cara melakukan perhitungan untul mencari nilai sin(π/7) menggunakan Deret Taylor.
Pertemuan Kedua
- Tanggal : 10 September 2019
- Pengajar : Dr. Ir. Engkos Achmad Kokasih M.T.
Pseudocode adalah sebuah kode yang digunakan untuk menulis sebuah algoritma dengan cara yang bebas yang tidak terikat dengan bahasa pemrograman tertentu. Pseudo berarti imitasi dan code berarti kode yang dihubungkan dengan instruksi yang ditulis dalam bahasa komputer (kode bahasa pemrograman). Apabila diterjemahkan secara bebas, maka pseudocode berarti tiruan atau imitasi dari kode bahasa pemrograman.
Pseudo code sinus
i=1, err=1; suku=x sin=suku while err>1e-7
ratio=-(x^2)/(2*i)/(2*i+1)
suku=suku*ratio
err=abs(suku/sin)
sin=sin+suku
i=i+1
Pseudo code kosinus
i=1, err=1; suku=1 cos=suku while err>1e-7
ratio=-(x^2)/(2*i)/(2*i-1)
suku=suku*ratio
err=abs(suku/cos)
cos=cos+suku
i=i+1
Pseudo code eksponensial
i=1, err=1; suku=1 exp=suku while err>1e-7
ratio=(x^2)/i
suku=suku*ratio
err=abs(suku/exp)
exp=exp+suku
i=i+1
Setelah itu membahas bahasa pemograman. Bahasa Pemrograman merupakan sebuah instruksi untuk memerintah komputer agar bisa menjalankan fungsi tertentu, namun hanya instruksi standar saja.Fungsi dari bahasa pemrograman adalah untuk memerintahkan sebuah komputer agar bisa mengolah data sesuai dengan yang kita inginkan. Jadi, kendali sepenuhnya ada di tangan kita.
Jenis-jenis Bahasa Pemrograman, dimana bahasa pemrograman yang umum diketahui ialah: Pseudo Code, C++, C, Python, PHP, Visual Basic, Java, JavaScript.
Pertemuan Ketiga
- Tanggal : 17 September 2019
- Pengajar : Dr. Ir. Engkos Achmad Kokasih M.T. dan Hanif Furqan
Pada pertemuan ketiga Mata Kuliah Metode Numerik, kami mempelajari tentang Turunan Numerik. Turunan numerik berfungsi untuk mempermudah penurunan suatu persamaan yang rumit. Dalam penggunaannya, turunan numerik dianjurkan untuk dihitung dengan memakai komputer ataupun kalkulator, dikarenakan kompleksnya angka yang dihitung. Untuk menghitung turunan numerik, terdapat tiga pendekatan yang bisa digunakan, yaitu : Turunan maju (Forward), Turunan mundur (Backward), dan Turunan pusat atau tengah (Center).
Pertemuan Keempat
- Tanggal : 24 September 2019
- Pengajar : Dr. Ir. Engkos Achmad Kokasih M.T.
Pada pertemuan kali ini, kami mempelajari root finding algoritma, yang bertujuan untuk mencari sebuah bilangan pembuat nol dari sebuah persamaan atau fungsi. Pada pertemuan kali ini dicontohkan dengan 3 metode, yaitu Secant, Bisect, dan Newton-Raphson method.
Secant method adalah metode menggunakan garis secant (gradien garis yang melalui titik (x_0, f(x_0)) dan (x_1, f(x_1)))
Bisect method adalah metode membagi dua bagian, lalu memilih dari dua bagian ini dipilih bagian mana yang mengandung akar dan bagian yang tidak mengandung akar dibuang.
Newton-Raphson method adalah metode pencarian akar suatu fungsi f(x) dengan pendekatan satu titik, dimana fungsi f(x) mempunyai turunan.
Pertemuan Kelima
- Tanggal : 1 Oktober 2019
- Pengajar : Dr. Ir. Engkos Achmad Kokasih M.T.
Semua metode numerik memiliki truncation error, baik itu Newton-Raphson, finite element, finite difference dst., dan semua software memiliki truncation error. Untuk memperkecil truncation error, meshing harus dilakukan dengan partisi yang kecil. Apa itu meshing? meshing merupakan pembagian daerah yang dianalisis menjadi partisi-partisi yang sangat kecil, semakin kecil partisi tersebut, semakin akurat hasilnya. Walaupun demikian, hasil yang dihasilkan dari metode numerik tetap diskrit, walaupun terlihat kontinum jika partisinya sangat kecil. Tetapi tidak selalu demikian kasusnya, jika partisi terlalu kecil, maka jumlah iterasi akan semakin banyak, artinya jumlah pengoperasian perhitungan bertambah banyak, dan jumlah rounding akan semakin banyak sehingga rounding error semakin besar. Jadi, untuk menentukan sebesar apa partisinya, ada nilai optimumnya. Untuk mengetahui nilai N (jumlah iterasi) yang paling optimum, nilai iterasi divariasikan dari kecil hingga besar, saat dia sudah tidak berubah banyak maka di titik tersebut lah jumlah iterasinya paling optimum. Begitu juga dengan jumlah mesh perlu divariasikan agar mendapat nilai yang paling optimum.
Pekerjaan Rumah
- Tanggal : 29 Oktober 2019
- Pengajar : Dr. Ahmad Indra Siswantara
Penyelesaian soal menggunakan model Governing equation pada mobil yang memiliki percepatan, gesekan, dan hambatan udara adalah:
F = m*a
F gesek = m*g*cf
F hambat = 0.5*cd*rho*area*vt^2
Percepatan total didapatkan dengan membagi ketiga gaya tersebut dengan massa
a tot = (F - (F gesek + F hambat))/m
a tot = v(t)/t
t= v(t) / ((F - (F gesek + F hambat))/m)
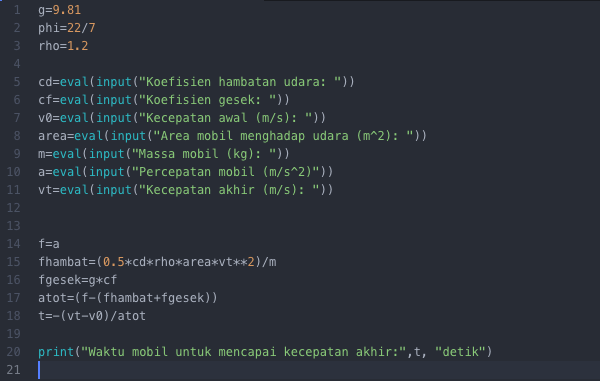
Pseudocode
Berikut adalah pseudocode untuk mencari kecepatan maksimum dan pada waktu berapa.
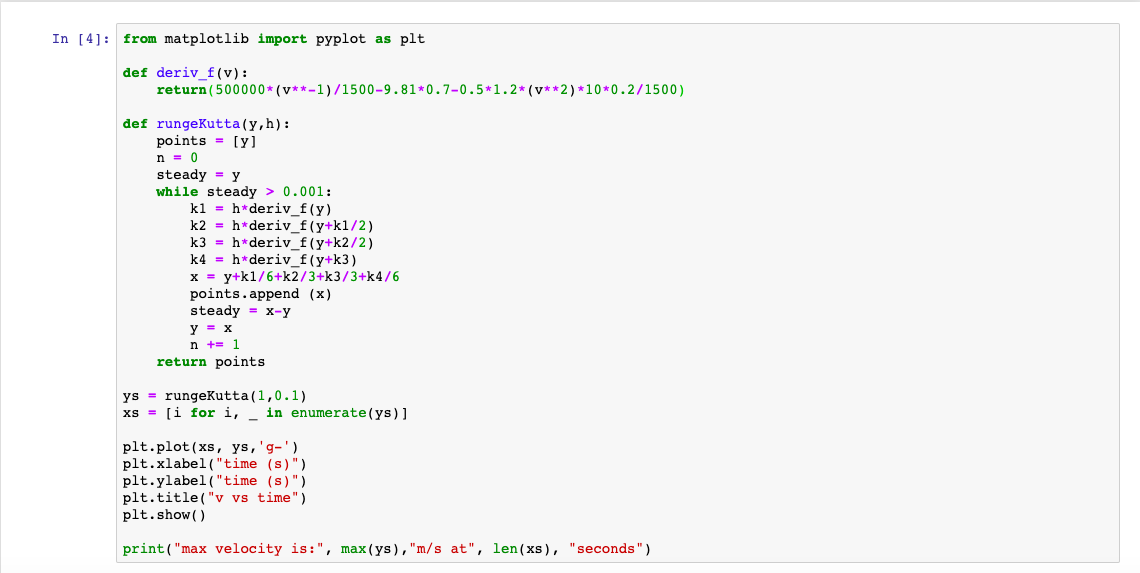
Program Python
Dengan menggunakan metode runge-kutta, berikut adalah program kami dari python
Untuk variable yang digunakan untuk simulasi berupa:
- Power= 500 KW
- Massa= 1500 kg
- Percepatan gravitasi= 9.81 m/s^2
- Koefisien gesek= 0.7
- Massa jenis= 1.2 kg/m^2
- Area= 10 m^2
- Koefisien drag= 0.2
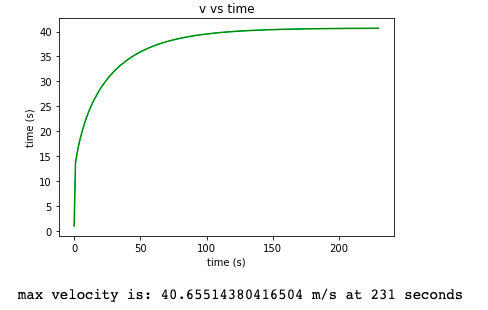
Grafik dan Hasil
Berikut adalah hasil grafik serta angka kecepatan dan waktu maksimum
Pertemuan Selasa, 12 November 2019
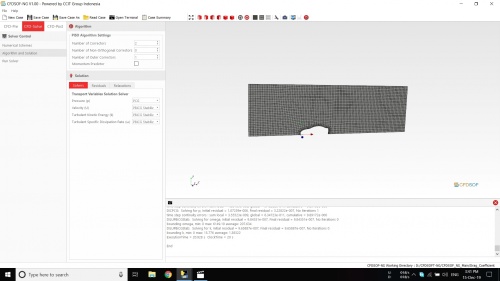
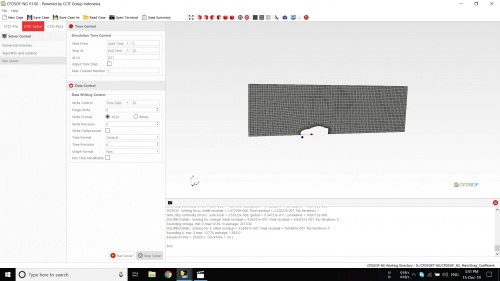
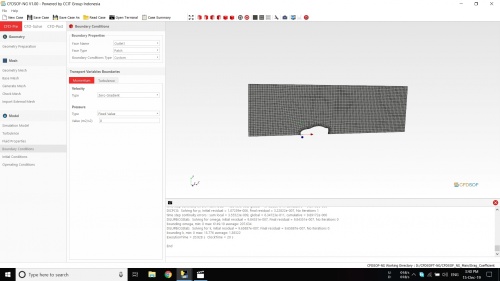
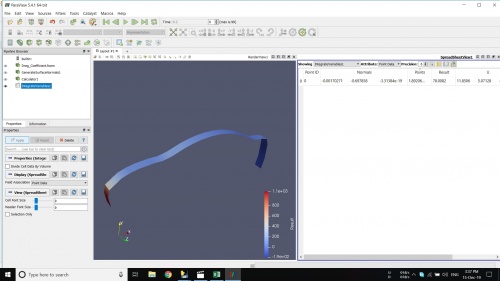
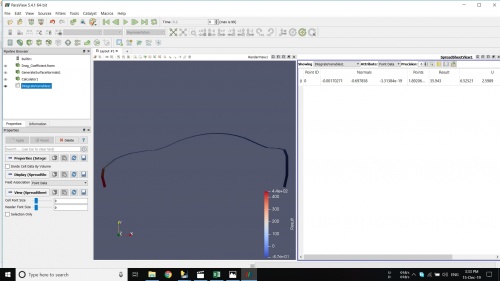
Pada pertemuan ini kami diajarkan cara menggunakan CFDSOF khususnya cara menganalisis suatu fluida yang berjalan pada suatu mobil. Hasil dari simulasi ini kemudian dijadikan tugas kelompok dimana mencari rumus persamaan gaya hambat dari kecepatan.
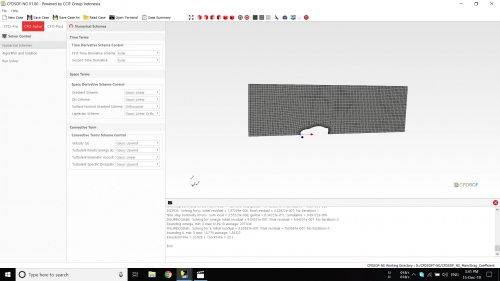
Simulasi CFDSOF
Untuk mendapatkan gaya hambat untuk setiap kecepatan kami melakukan simulasi di CFDSOF. Untuk variabel kecepatannya ditentukan 5 variabel yaitu:
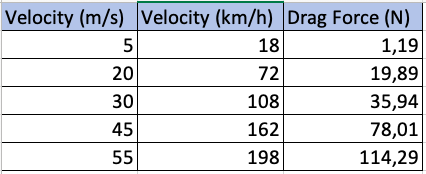
- 5 m/s atau 18 km/h untuk rata-rata kecepatan rush hour dalam kota
- 20 m/s atau 72 km/h untuk rata-rata kecepatan non-rush hour dalam kota
- 30 m/s atau 108 km/h untuk rata-rata kecepatan pada tol
- 45 m/s atau 162 km/h untuk kecepatan maksimal mobil biasa
- 55 m/s atau 198 km/h untuk kecepatan maksimal mobil sport
Berikut adalah proses simulasi yang kami lakukan dengan aplikasi CFDSOF
Tabel Hasil Data
Dari data yang didapatkan dari CFDSOF kami masukkan ke dalam tabel berikut
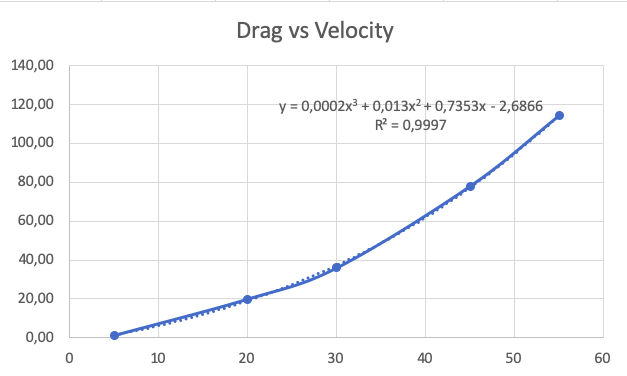
Plotting Kurva dan Rumus Hambat
Kemudian kami melakukan plotting kecepatan terhadap gaya hambat menjadi sebuah kurva, berikut adalah hasilnya
Dari kurva diatas, didapatkan bahwa rumus untuk gaya drag adalah y = 0,0002x3 + 0,013x2 + 0,7353x - 2,6866
Dengan y adalah gaya drag dan x adalah kecepetan, sehingga didapatkan rumus akhir Fd = 0,0002v3 + 0,013v2 + 0,7353v - 2,6866
Pertemuan Selasa, 26 November 2019
Pada pertemuan ini, Pak Ahmad Indra memberikan kuis yang menyangkut pengertian kami mengenai metode numerik.
Selasa, 3 Desember 2019
Pada pertemuan ini, beberapa kelompok mempresentasikan mengenai optimasi airfoil yang mereka lakukan. Kemudian dijelaskan mengenai neural network yaitu sebuah jaringan neuron yang berfungsi seperti otak manusia, dimana setelah dilatih dapat memprediksi hal-hal.
ANN Adalah sistem pembelajaran terawasi yang dibangun dari sejumlah besar elemen sederhana, yang disebut neuron atau perceptron. Setiap neuron dapat membuat keputusan sederhana, dan memberi makan keputusan itu ke neuron lain, yang diorganisasikan dalam lapisan yang saling berhubungan.
Jika kita tidak menerapkan fungsi Aktivasi maka sinyal output hanya akan menjadi fungsi linier sederhana. Fungsi linier hanyalah polinomial satu derajat.
Contoh dari fungsi Aktivasi, yaitu :
- Sigmoid
- Tanh
- ReLu
- LeakyReLu
- SoftMax
Backpropagation adalah algoritma pembelajaran untuk memperkecil tingkat error dengan cara menyesuaikan bobotnya berdasarkan perbedaan output dan target yang diinginkan. Backpropagation juga merupakan sebuah metode sistematik untuk pelatihan multilayer.
Secara umum algoritmanya terdiri dari tiga langkah utama, yaitu :
- Pengambilan input
- Penelusuran error
- Penyesuaian bobot