Difference between revisions of "Muhammad Syariifi Muflih"

From ccitonlinewiki
Jump to: navigation, search
 
Line 386: Line 386:
  
  
−
Dapat dilihat di: [[Kelompok 14]]
+
 
 +
=== Airfoil ===
 +
 
 +
Pada tugas kali ini, kami mendesain sebuah airfoil dengan menggunakan program Autodesk Inventor untuk dites seberapa besar gaya angkat (lift force) dan gaya hambatan udara (drag force) yang dihasilkan ketika menabrak udara dengan kecepatan 100 m/s. Berikut adalah bentuk desain airfoil yang kami buat:
 +
 
 +
[[File:Airfoil_kelompok_14.png]]
 +
 
 +
 
 +
 
 +
=== Data Drag Force & Lift Force ===
 +
 
 +
Dengan menggunakan software CFDSOF-NG V1.00, diperoleh data besarnya drag force & lift force terhadap kemiringan sudut airfoil sebagai berikut:
 +
 
 +
[[File:Data_airfoil_kelompok_14.png]]
 +
 
 +
 
 +
 
 +
=== Kurva drag force & lift force terhadap kemiringan sudut airfoil ===
 +
 
 +
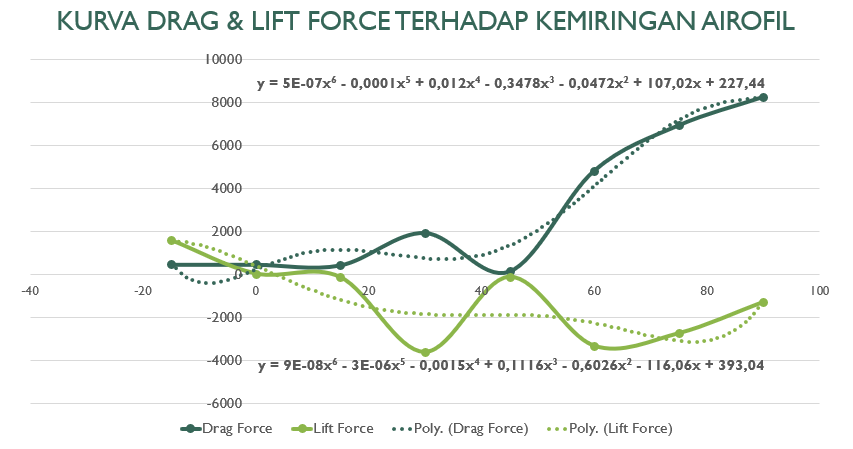
Berikut kurva dari drag force & lift force terhadap kemiringan sudut airfoil:
 +
 
 +
[[File:Kurva_airfoil_kelompok_14.png]]
 +
 
 +
 
 +
 
 +
=== Optimasi ===
 +
 
 +
Dari persamaan kurva tersebut, kami mencari nilai optimasi dari masing-masing force dengan menggunakan kode berikut:
 +
 
 +
import numpy as np
 +
from scipy.optimize import minimize
 +
 +
def cdrag(x):
 +
    x1 = x[0]
 +
    drag = 0.0000005*x1**6-0.0001*x1**5+0.012*x1**4-0.3478*x1**3-0.0472*x1**2+107.02*x1+227.44
 +
    return drag
 +
 +
def clift(x):
 +
    x1 = x[0]
 +
    lift = 0.00000009*x1**6-0.000003*x1**5-0.0015*x1**4+0.1116*x1**3-0.6026*x1**2-116.06*x1+393.04
 +
    return lift
 +
 +
def objective(x):
 +
    return cdrag(x)
 +
 +
def constraint1(x):
 +
    return 90 - cdrag(x)
 +
def constraint2(x):
 +
    return 90 - clift(x)
 +
 +
con1=({'type':'ineq','fun':constraint1})
 +
con2=({'type':'ineq','fun':constraint2})
 +
cons = (con1,con2)
 +
 +
x1_guess = 50
 +
 +
x0 = np.array([x1_guess])
 +
 +
sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True})
 +
 +
xopt = sol.x
 +
forceopt = -sol.fun
 +
 +
dragopt = cdrag(xopt)
 +
liftopt = clift(xopt)
 +
 +
print ("")
 +
print ("Hasil optimasi:")
 +
print ("Sudut optimal = "+str(-xopt[0]))
 +
print ("Total force optimal = "+str(forceopt))
 +
print ("Drag force optimal = "+str(-dragopt))
 +
print ("Lift force optimal = "+str(liftopt))
 +
 
 +
'''Hasil optimasi''':
 +
 +
Sudut optimal = -18.824361039981582 °
 +
Total force optimal = -1197.981206594249 N
 +
Drag force optimal = -1197.981206594249 N
 +
Lift force optimal = -1452.2582614781118 N
  
 
<comments voting"plus" />
 
<comments voting"plus" />

Latest revision as of 17:11, 17 December 2019

Riifi di tahun 2019

Muhammad Syariifi Muflih (lahir di Jakarta, 26 Agustus 2000) adalah mahasiswa Fakultas Teknik Universitas Indonesia jurusan Teknik Mesin angkatan 2018. Setelah mengikuti kuliah selama dua semester, saya mengambil mata kuliah Metode Numerik di semester 3 dan mengisi halaman yang Anda lihat sekarang ini.

Kelas Metode Numerik

Mengapa Harus Belajar Kalkulus?

Menurut saya, seorang mahasiswa Teknik Mesin harus mempelajari kalkulus karena merupakan dasar menghitung untuk berbagai macam masalah di dalam mata kuliah Fisika Dasar, Statika Struktur, Mekanika Kekuatan Material, Kinematika & Dinamika, dan lainnya yang memperlukan kalkulasi.

Apa itu Python?

Python adalah salah satu jenis bahasa pemrograman yang digunakan untuk membuat program dengan tujuan menyelesaikan suatu masalah.

Contoh bahasa pemrograman Python untuk memprogram robot menggambar hexagon


Belajar Python

Pertama-tama sebelum memulai mempelajari python, saya mengunduh python terlebih dahulu di http://www.python.org/downloads. Setelah python diinstall, python dapat digunakan dengan program text editor untuk menulis code-code python seperti Notepad, namun ada text editor yang digunakan khusus untuk menulis code-code python yang dinamakan IDE (Integrated Development Environment). Salah satu IDE tersebut adalah PyCharm, yang saya unduh di https://www.jetbrains.com/pycharm. Di dalam PyCharm, create new project untuk membuat project baru, kemudian klik kanan di folder project tersebut -> New -> Python file.

Istilah-istilah dasar dalam Python

String = Text di antara kedua tanda kutip ("). Contoh string: "Belajar Python"

Number = Angka di antara kedua tanda kutip ("). Contoh number: "50" , "3.14"

Variable = Container yang bisa menyimpan nilai data tertentu. Suatu nilai data dapat disimpan di dalam variable. Untuk membuat variabel: *masukkan nama variable* = *data yang ingin diinput*. Nama variabel tidak boleh ada spasi namun dapat diganti dengan underscore (_). Contoh variable: character_name = Muhammad Syariifi Muflih

Membuat kalkulator sederhana dengan Python

Terdapat 2 jenis angka:

Int (integer) = bilangan bulat (tidak termasuk pecahan/desimal)

Float = bilangan yang termasuk pecahan/desimal

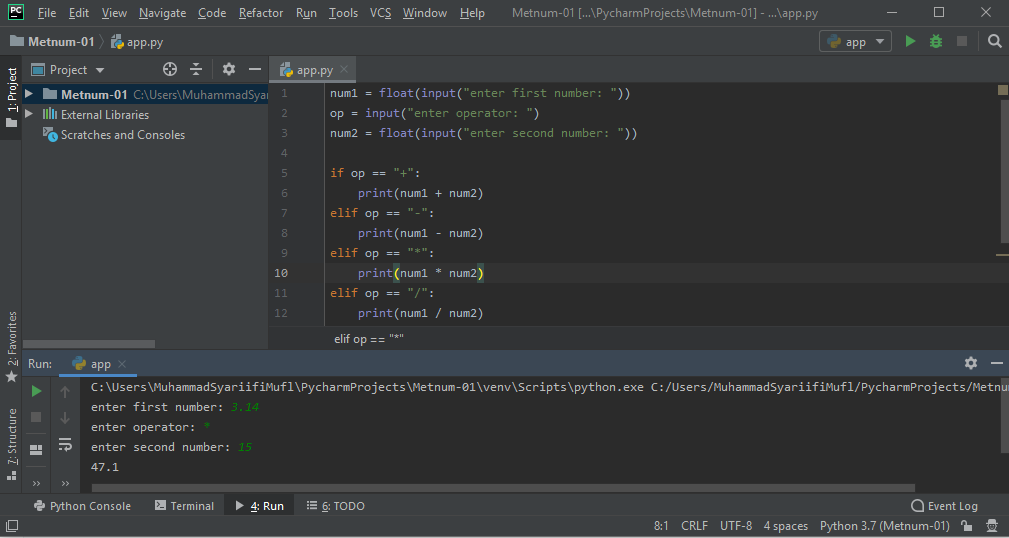
Untuk membuat kalkulator ini, saya menggunakan 3 variable, 1 untuk angka pertama, 1 untuk angka kedua, dan 1 untuk operator (+ - x /) 

num1 = float(input("enter first number: "))
op = input("enter operator: ")
num2 = float(input("enter second number: "))
if op == "+":
   print(num1 + num2)
elif op == "-":
   print(num1 - num2)
elif op == "*":
   print(num1 * num2)
elif op == "/":
   print(num1 / num2)
else:
   print("Invalid operator")

Setelah code-code di atas tertulis, klik Run dan kalkulator siap digunakan untuk operasi + - x /

Basic calc python.png


Menghitung (x^2-1)/(x-1) dengan Python

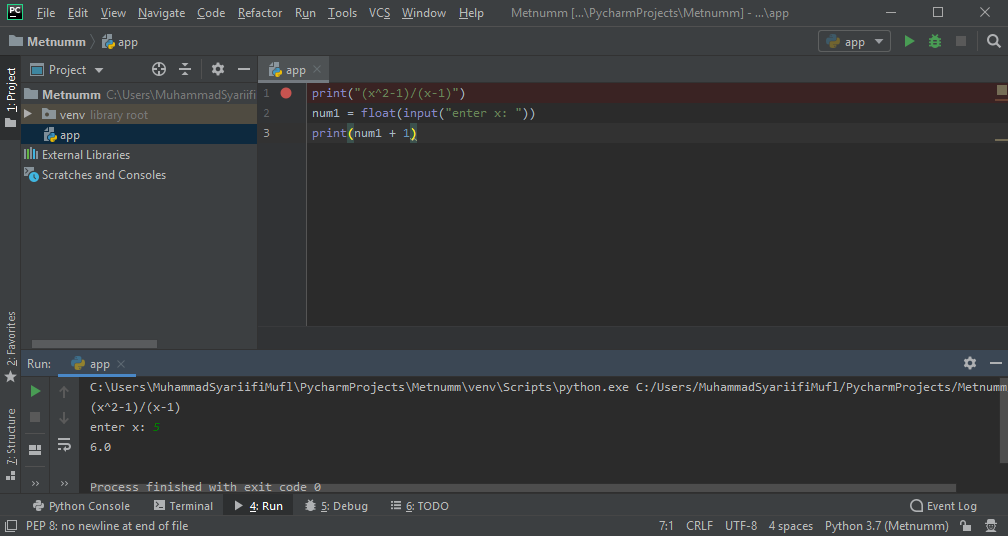
Karena soal tersebut jika dihitung akan menghasilkan x + 1 , maka berikut adalah code yang saya gunakan untuk menghitung soal di atas dengan Python: 

print("(x^2-1)/(x-1)")
num1 = float(input("enter x: "))
print(num1 + 1)

(x^2-1)bagi(x-1).png


Python Tuples

tuple = ("Muhammad","Syariifi","Muflih","Riifi",(26,8,2000))
name1,name2,name3,surname,born = tuple
print("Nama saya",name1,name2,name3,", biasa dipanggil",surname,". Saya muncul di bumi pada tanggal",born[0],"bulan",born[1],"tahun",born[2],".")

Run kode di atas menghasilkan: 

Nama saya Muhammad Syariifi Muflih , biasa dipanggil Riifi . Saya muncul di bumi pada tanggal 26 bulan 8 tahun 2000 .


Python Lists

matakuliah = ["Termodinamika", "Visualisasi Permodelan Mesin", "Metode Numerik"]
print("Mata kuliah hari Rabu:")
for x in matakuliah:
 print(x)

Run kode di atas menghasilkan: 

Mata kuliah hari Rabu:
Termodinamika
Visualisasi Permodelan Mesin
Metode Numerik


Menentukan Suku Ke-n Deret Fibonacci dengan Python

Algoritma

1. Mulai

2. Tentukan definisi n

3. Tentukan nilai a=0 , b=1

4. Jika n<0, print "Incorrect input"

5. Dan jika n=0, kembali ke a

6. Dan jika n=1, kembali ke b

7. Selain itu, untuk i di range 2 dan seterusnya: c = a + b, a = b, b = c, return b

8. Input nilai n

9. Selesai


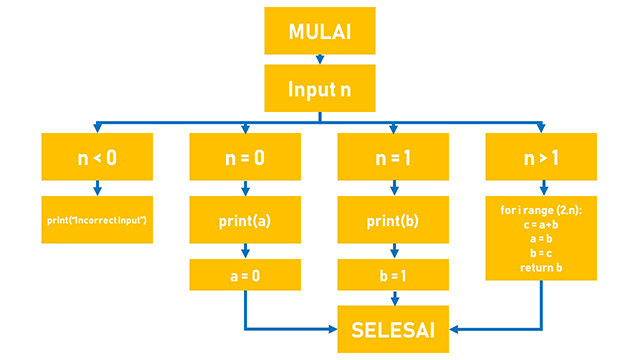
Flowchart

Flowchart fibonacci muhammad.syariifi.jpg


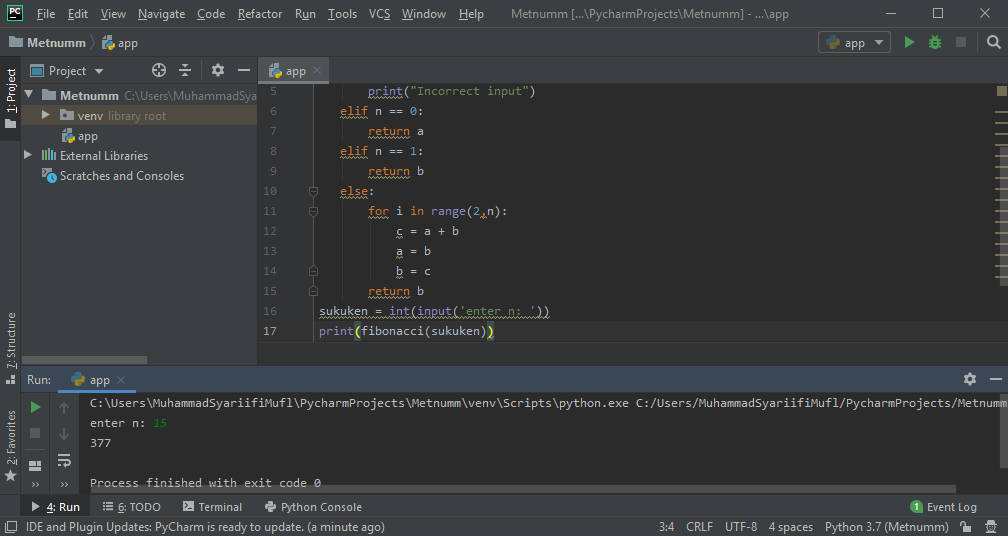
Kode di Python

def fibonacci(n):
   a = 0
   b = 1
   if n < 0:
       print("Incorrect input")
   elif n == 0:
       return a
   elif n == 1:
       return b
   else:
       for i in range(2,n):
           c = a + b
           a = b
           b = c
       return b
sukuken = int(input('enter n: '))
print(fibonacci(sukuken))

Fibonacci muhammad.syariifi.png

Run dari kode di atas. Ketika dimasukkan nilai n = 15, program menampilkan suku ke-15 dari deret fibonacci yaitu 377.


QUIZ 16 Oktober 2019

Problem 2.1 No. 6 Hlm. 55

from numpy import linalg
import numpy as np
A = np.array([[0, 0, 2, 1, 2],  # input matriks A
             [0, 1, 0, 2, -1],
             [1, 2, 0, -2, 0],
             [0, 0, 0, -1, 1],
             [0, 1, -1, 1, -1]])
B = np.array([[1],    # input matriks B
             [1],
             [-4],
             [-2],
             [-1]])
hasil = np.linalg.solve(A, B)  # operasi aljabar
print(hasil)  # memperlihatkan hasil

Hasil dari soal menggunakan run kode di atas: [2, -2, 1, 1, -1]

Problem 7.1 No. 2 Hlm. 263

x0 = 0  # x0 dan y sebagai titik asal, x yaitu 0.03 (diminta soal), dan h sebagai tingkat peningkatan
y = 1  # pada x = 0 , y = 1
h = 0.01  # di sini digunakan h = 0.01
x = 0.03

def dydx(x, y):  # dydx menyatakan persamaan awal di soal
  return (x**2 - 4*y)  # dari soal, y' = x^2 - 4y

def rangekutta(x0, y0, x, h):  # perhitungan range-kutta
  n = (int)((x - x0)/h)  
  y = y0 
  for i in range(1, n + 1): 
     k1 = h * dydx(x0, y)
     k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
     k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
     k4 = h * dydx(x0 + h, y + k3)
     y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)  # untuk y selanjutnya
     x0 = x0 + h  # untuk x selanjutnya
  return y 

print("Nilai y(", x, ") :", rangekutta(x0, y, x, h)) # memperlihatkan nilai y pada x = 0.03

Hasil dari soal menggunakan run kode di atas: Nilai y(0.03) : 0.8869291754400297


UTS 23 Oktober 2019

Muhasabah


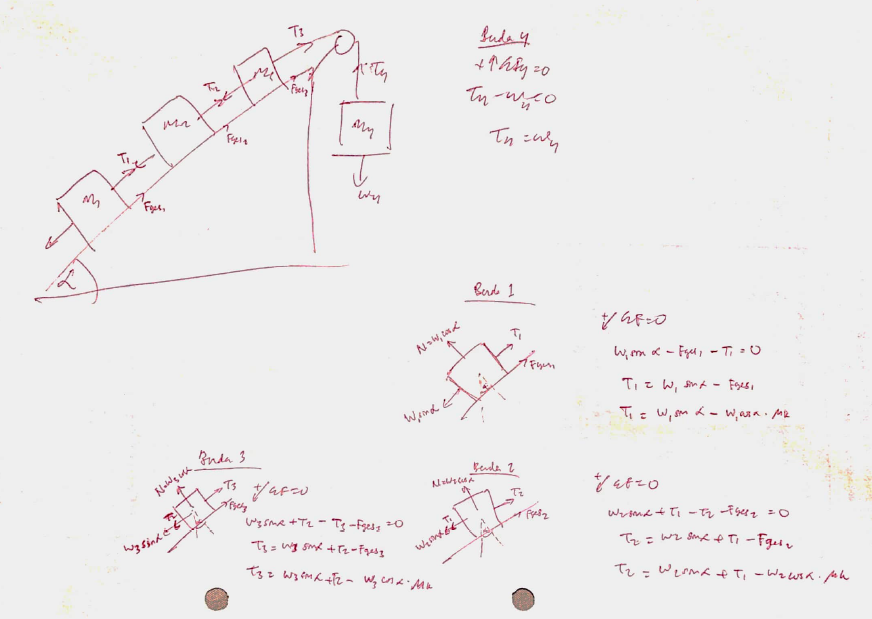
Soal A : Mencari T1, T2, T3, T4 jika diketahui m1, m2, m3, m4

Uts soal a muhammad.syariifi.png


Berikut kode yang saya gunakan untuk menghitung T1, T2, T3, T4 seperti perhitungan di atas: 

import math

m1 = float(input('Massa M1 (dalam kg): '))   #Menginput nilai m1
m2 = float(input('Massa M2 (dalam kg): '))   #Menginput nilai m2
m3 = float(input('Massa M3 (dalam kg): '))   #Menginput nilai m3
m4 = float(input('Massa M4 (dalam kg): '))   #Menginput nilai m4
g = float(input('Gravitasi (dalam m/s^2): '))   #Menginput nilai g
alfa = float(input('Kemiringan bidang miring (dalam derajat): '))   #Menginput nilai alfa (sudut kemiringan)

cosalfa = math.cos(math.radians(alfa))   #perhitungan cos alfa
sinalfa = math.sin(math.radians(alfa))   #perhitungan sin alfa

w1 = m1 * g   #perhitungan w1
w2 = m2 * g   #perhitungan w2
w3 = m3 * g   #perhitungan w3
w4 = m4 * g   #perhitungan w4

N1 = w1 * cosalfa   #perhitungan gaya normal benda 1
N2 = w2 * cosalfa   #perhitungan gaya normal benda 2
N3 = w3 * cosalfa   #perhitungan gaya normal benda 3

koefisien = float(input("Koefisien gesek: "))   #menginput koefisien gesek

Fges1 = N1 * koefisien   #perhitungan gaya gesek 1
Fges2 = N2 * koefisien   #perhitungan gaya gesek 2
Fges3 = N3 * koefisien   #perhitungan gaya gesek 3

F1 = w1 * sinalfa   #perhitungan gaya menurun benda 1 (F1)
F2 = w2 * sinalfa   #perhitungan gaya menurun benda 2 (F2)
F3 = w3 * sinalfa   #perhitungan gaya menurun benda 3 (F3)

T1 = F1 - Fges1        #perhitungan T1
T2 = F2 - Fges2 + T1   #perhitungan T2
T3 = F3 - Fges3 + T2   #perhitungan T3
T4 = w4                #perhitungan T4

print("Nilai T1 (dalam Newton) :", T1)   #menampilkan nilai T1
print("Nilai T2 (dalam Newton) :", T2)   #menampilkan nilai T2
print("Nilai T3 (dalam Newton) :", T3)   #menampilkan nilai T3
print("Nilai T4 (dalam Newton) :", T4)   #menampilkan nilai T4

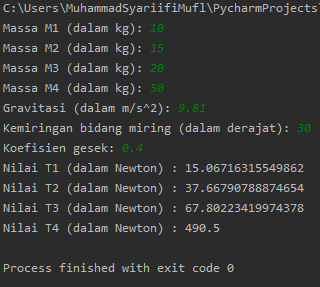
Berikut contoh run dari kode di atas:

Run uts soal a muhammad.syariifi.png


Video penjelasan:


Soal B : Mencari t yang diperlukan mobil dari diam hingga mencapai top speed

Uts soal b muhammad.syariifi.jpg


Berikut kode yang saya gunakan untuk menghitung t yang diperlukan mobil dari diam hingga mencapai top speed (diketahui) seperti perhitungan di atas: 

Torsimesin = float(input('Torsi dari mesin (Nm): '))   #menginput nilai torsi dari mesin di ban
Ukuranban = float(input('Ukuran ban (inch): '))        #menginput diameter ukuran ban dalam inch
massamobil = float(input('Massa mobil (kg): '))        #menginput massa mobil

g = float(input('Gravitasi (m/s^2): '))                #menginput nilai gravitasi
N = massamobil * g                                     #perhitungan gaya normal
koefgesek = float(input('Koefisien gesek: '))          #menginput koefisien gesek jalanan
Fgesek = N * koefgesek                                 #perhitungan gaya gesek

RUB = Ukuranban * 0.0254 / 2                           #mengkonversi diameter ban dalam inch ke jari-jari dalam meter
Froda = Torsimesin / RUB                               #perhitungan gaya ke depan dari roda

if Fgesek > Froda:                                     #jika gaya gesek lebih besar dari gaya roda, mobil dapat melaju
   kmh = float(input('Top speed (km/h): '))            #menginput nilai top speed dalam km/h
   topspeed = kmh / 3.6                                #mengkonversi top speed dari km/h ke m/s

   Cd = float(input('Coefficient of drag: '))          #menginput coefficient of drag
   A = float(input('Area (m^2): '))                    #menginput luas area drag
   rho = float(input('Massa jenis udara (kg/m^3): '))  #menginput massa jenis udara
   Fdrag = Cd * A * rho * topspeed ** 2 / 2            #perhitungan gaya drag

   atot = (Froda - Fdrag) / massamobil                 #perhitungan a total, yaitu a dari roda dikurang a dari drag

   t = topspeed / atot                                 #perhitungan t
   print('t (s): ', t)                                 #menampilkan nilai t

if Froda > Fgesek:
   print('Torsi mobil terlalu besar sehingga ban berdecit')

#jika gaya gesek lebih kecil dari gaya roda, ban berdecit sehingga mobil tidak dapat melaju

Berikut contoh run dari kode di atas:

Run uts soal b muhammad.syariifi.png


Video penjelasan:


Contoh soal dengan menggunakan metode Runge-Kutta Orde Ke-4

Soal dan penyelesaian

Metnum 05-11-2019 muhammad.syariifi.jpg

Dari soal tersebut, setelah mempertimbangkan gaya hambatan udara (Fdrag), nilai v (kecepatan) pada t (waktu) tertentu dapat ditemukan dengan metode Runge-Kutta Orde Ke-4, dengan persamaan a = 2145 t - 0.0000179 v^2 untuk 0 <= t < 0.1, dan a = 214.5 t - 0.0000179 v^2 untuk t >= 0.1

Dengan menggunakan python: 

# t0 dan v0 sebagai keadaan awal, t sebagai t yang diinput, dan h sebagai increment
t0 = 0
v0 = 0
h = 0.01   # di sini digunakan h = 0.01
t = float(input("Nilai t: "))  # perintah untuk memasukkan nilai t

if 0 <= t < 0.1:  # untuk 0 <= t < 0.1
   def F(t, v):
       return (2145 * t - 0.0000179 * (v**2))  # persamaan a yang telah diperoleh

   def rungeKutta(t0, v0, t, h):  # perhitungan Runge-Kutta
       n = (int)((t - t0) / h)
       v = v0
       for i in range(1, n + 1):
           k1 = h * F(t0, v)
           k2 = h * F(t0 + 0.5 * h, v + 0.5 * k1)
           k3 = h * F(t0 + 0.5 * h, v + 0.5 * k2)
           k4 = h * F(t0 + h, v + k3)
           v = v + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
           t0 = t0 + h
       return v

   print("Nilai v pada t =", t, "adalah", rungeKutta(t0, v0, t, h), "m/s")  # menampilkan nilai v

elif t >= 0.1:  # untuk t >= 0.1
   def F(t, v):
       return (214.5 - 0.0000179 * (v**2))  # persamaan a yang telah diperoleh

   def rungeKutta(t0, v0, t, h):  # perhitungan Runge-Kutta
       n = (int)((t - t0) / h)
       v = v0
       for i in range(1, n + 1):
           k1 = h * F(t0, v)
           k2 = h * F(t0 + 0.5 * h, v + 0.5 * k1)
           k3 = h * F(t0 + 0.5 * h, v + 0.5 * k2)
           k4 = h * F(t0 + h, v + k3)
           v = v + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4)
           t0 = t0 + h
       return v

   print("Nilai v pada t =", t, "adalah", rungeKutta(t0, v0, t, h), "m/s")  # menampilkan nilai v

else:
   print("Nilai t harus positif.")

Berikut run dari kode di atas:

Metnum 05-11-2019-2 muhammad.syariifi.png

ketika t = 2 s, nilai v adalah 426.81718605720295 m/s

Video pembahasan


Optimasi Angle of Attack pada Airfoil

Airfoil

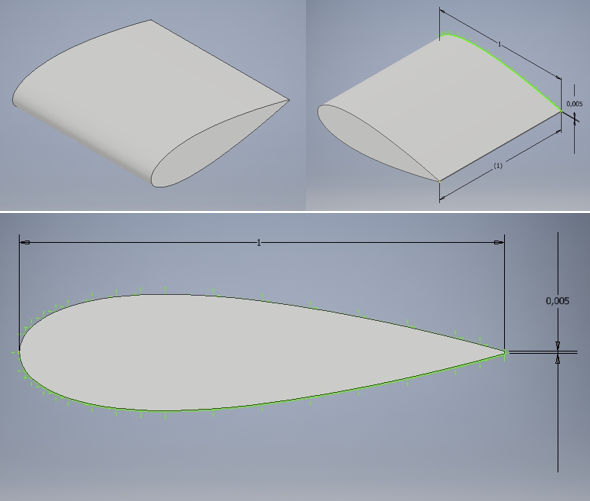
Pada tugas kali ini, kami mendesain sebuah airfoil dengan menggunakan program Autodesk Inventor untuk dites seberapa besar gaya angkat (lift force) dan gaya hambatan udara (drag force) yang dihasilkan ketika menabrak udara dengan kecepatan 100 m/s. Berikut adalah bentuk desain airfoil yang kami buat:

Airfoil kelompok 14.png


Data Drag Force & Lift Force

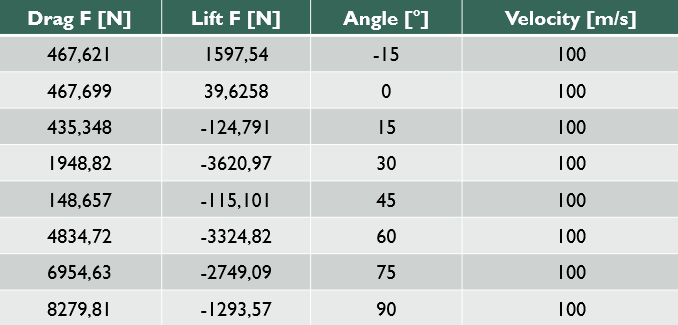
Dengan menggunakan software CFDSOF-NG V1.00, diperoleh data besarnya drag force & lift force terhadap kemiringan sudut airfoil sebagai berikut:

Data airfoil kelompok 14.png


Kurva drag force & lift force terhadap kemiringan sudut airfoil

Berikut kurva dari drag force & lift force terhadap kemiringan sudut airfoil:

Kurva airfoil kelompok 14.png


Optimasi

Dari persamaan kurva tersebut, kami mencari nilai optimasi dari masing-masing force dengan menggunakan kode berikut: 

import numpy as np
from scipy.optimize import minimize

def cdrag(x):
   x1 = x[0]
   drag = 0.0000005*x1**6-0.0001*x1**5+0.012*x1**4-0.3478*x1**3-0.0472*x1**2+107.02*x1+227.44
   return drag

def clift(x):
   x1 = x[0]
   lift = 0.00000009*x1**6-0.000003*x1**5-0.0015*x1**4+0.1116*x1**3-0.6026*x1**2-116.06*x1+393.04
   return lift

def objective(x):
   return cdrag(x)

def constraint1(x): 
   return 90 - cdrag(x)
def constraint2(x):
   return 90 - clift(x)

con1=({'type':'ineq','fun':constraint1})
con2=({'type':'ineq','fun':constraint2})
cons = (con1,con2)

x1_guess = 50

x0 = np.array([x1_guess]) 

sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True})

xopt = sol.x
forceopt = -sol.fun 

dragopt = cdrag(xopt)
liftopt = clift(xopt) 

print ("")
print ("Hasil optimasi:")
print ("Sudut optimal = "+str(-xopt[0]))
print ("Total force optimal = "+str(forceopt))
print ("Drag force optimal = "+str(-dragopt))
print ("Lift force optimal = "+str(liftopt))

Hasil optimasi:

Sudut optimal = -18.824361039981582 °
Total force optimal = -1197.981206594249 N
Drag force optimal = -1197.981206594249 N
Lift force optimal = -1452.2582614781118 N


Aldy.cahya

61 months ago
Score 2++
Untuk menjelaskan maasing masing masalah yang ada di soal no A dan B UTS sudah menyeluruh dan mudah dimengerti juga dapat menyelesaikan masalah yang diberikan

Permalink | Reply

Anonymous user #1

30 months ago
Score 0 You

bang kalo nilai 80-100 : A nilai 60 - 79 : B nilai 40 - 59 : C dibawahnya : D

nilaiKelas = [100,99,75,77,20]

list ini dimasukin ke for looping, yg didalamnya ada if else menentukan nilai akhir.

for looping if else

gimana ya ? tolong pencerahannya

Permalink | Reply

Add your comment
ccitonlinewiki welcomes all comments. If you do not want to be anonymous, register or log in. It is free.

Retrieved from "http://air.eng.ui.ac.id/index.php?title=Muhammad_Syariifi_Muflih&oldid=18488"