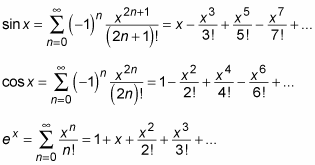Difference between revisions of "Muhammad Ichsan"
(→Pertemuan 5 (1 oktober 2019)) |
|||
| Line 118: | Line 118: | ||
print("waktu mobil untuk mencapai top speed: ",t, "detik") | print("waktu mobil untuk mencapai top speed: ",t, "detik") | ||
| + | |||
| + | =='''Pertemuan 7 (5 november 2019)'''== | ||
| + | Pada pertemuan kali ini, kita membahas tentang metode runge-kutta. Metode Runge Kutta adalah metode penyelesaian masalah nilai awal persamaan diferensial dengan pendekatan iterasi numerik. Metode Runge-Kutta adalah alternatif lain dari metode deret Taylor yang tidak membutuhkan perhitungan turunan. Metode ini berusaha mendapatkan derajat ketelitian yang lebih tinggi. | ||
Revision as of 16:33, 9 December 2019
Contents
Profil
Nama: Muhammad Ichsan
NPM: 1706036122
Jurusan: Teknik Mesin
Pertemuan 1 (03 september 2019)
Pada pertemuan pertama diawali dengan penjelasan singkat tentang apa itu Metode Numerik. Kelas Metode Numerik merupakan kelas lanjutan dari Kalkulus, Aljabar Linear, dan Matematika Teknik. Setelah menjelaskan tentang metode numerik, dilanjutkan membahas tentang Taylor's Method. Deret Taylor adalah representasi fungsi matematika sebagai jumlahan tak hingga dari suku-suku yang nilainya dihitung dari turunan fungsi tersebut di suatu titik.
Setelah menjelaskan tentang deret taylor, kita diminta untuk mencari nilai dari sin (phi/7) dengan deret taylor mengunakan microsoft excel.
Pertemuan 2 (10 september 2019)
Pada pertemuan kedua diawali dengan penjelasan tentang bahasa pemograman. Bahasa pemograman adalah media instruksi komputer untuk menjalankan perintah yang diberikan. Kemudian kita membahas tentang bahasa pemograman yang paling dasar, yaitu bahasa binary atau biasa disebut bahasa mesin. Bahasa binary hanya menggunakan angka 1 dan 0. Angka-angka tersebut lalu dikombinasikan dan diurutkan sehingga susunanya dapat menggambarkan suatu perintah untuk dijalankan oleh komputer. Bahasa binary ini digunakan oleh komputer karena komputer akan lebih cepat membaca perintah hanya dengan membaca kombinasi angka-angka binary. Karena bahasa binary memiliki banyak kombinasi yang sangat sulit dimengerti oleh manusia, maka dibuatlah bahasa penerjemah yang mudah dibaca oleh manusia. Lalu bahasa tersebut akan diterjemahkan lagi oleh komputer, yang biasa disebut dengan compiler.
Setelah itu, Pak Engkos menjelaskan tentang psuedo code. Pseudo code adalah deskripsi dari algoritma pemrograman komputer yang menggunakan konvensi struktural dari suatu bahasa pemrograman, dan ditujukan agar dapat dibaca oleh manusia dan bukan oleh mesin. Berikut ini adalah contoh untuk mencari nilai sin x menggunakan psuedo code.
I = r ; err = 1
suku = x
sin = suku
while err > 1e-7
{ ratio = -x^2/((2*I)*(2*I+1))
suku = suku*ratio
err = abs(suku/sin)
sin = sin + suku
I = I+1 }
Pertemuan 3 (17 september 2019)
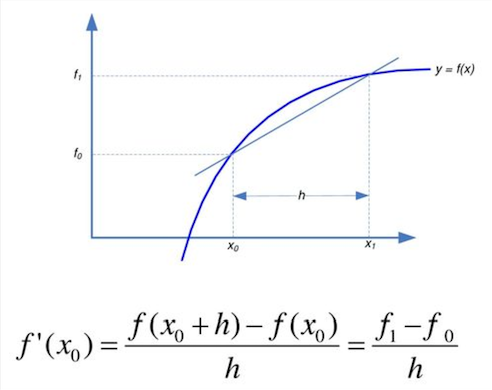
Pada pertemuan kali ini materi yang dibahas adalah turunan numerik. Persoalan turunan numerik ialah menentukan hampiran nilai turunan fungsi f yang diberikan dalam bentuk tabel. Ada 3 pendekatan dalam perhitungan turunan numerik, yaitu:
1. Pendekatan selisih maju
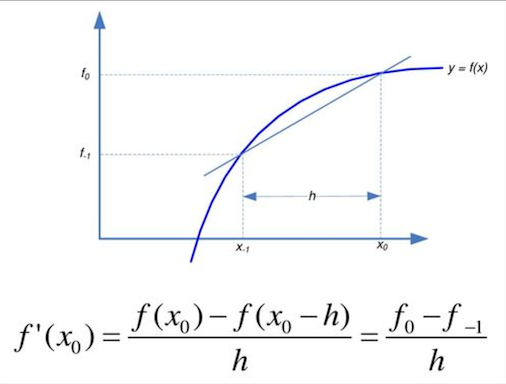
2. Pendekatan selisih mundur
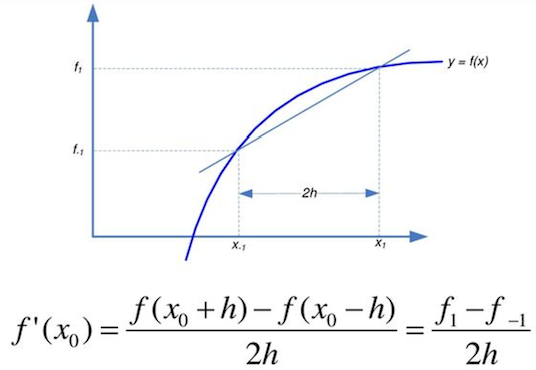
3. Pendekatan selisih pusat
Pertemuan 4 (24 september 2019)
Pada pertemuan kali ini materi yang dibahas adalah secant method, bisect method, dan newton-raphson method. Metode-metode ini digunakan untuk mencari bilangan pembuat nol dalam suatu fungsi atau biasa disebut dengan root-finding algorithm. Secant method adalah metode yang menggunakan garis secant untuk mengaproksimasi nilai sebuah fungsi. Bisect method merupakan metode pencarian akar-akar untuk fungsi yang kontinu. Newton-raphson method merupakan metode pencarian akar suatu fungsi dengan pendekatan satu titik, dimana fungsinya memiliki turunan.
Pertemuan 5 (1 oktober 2019)
Dalam melakukan suatu penurunan fungsi dan pengerjaan metode numerik terdapat beberapa error yang akan terjadi. Error yang sering terjadi adalah Round-off errors, Truncation errors, dan Range errors. Round-off errors adalah pembulatan angka menjadi dasar adanya kesalahan. Truncation errors adalah pemotongan suku pada suatu deret/rumus approksimasi menjadi pemicu kesalahan yang timbul, misalnya suatu rumus rumit diganti dengan rumus yang lebih sederhana. Range errors adalah kesalahan yang terjadi karena nilai hasil komputasi melampaui batas angka yang diperbolehkan oleh komputer, misalnya sangat kecil atau sangat besar. Semua metode numerik memiliki truncation error, baik itu Newton-Raphson, finite element, finite difference dst, dan semua software juga memiliki truncation error.
Pertemuan 6 (29 oktober 2019)
Pada pertemuan kali ini, kita membahas tentang bahasa pyhton yang merupakan salah satu bahasa dalam metode numerik. Beberapa hal diterangkan pada kesempatan ini, baik bahasa-bahasa tertentu, penulisan hingga praktik secara langsung menggunakan aplikasi yang ada. Python sendiri adalah salah satu metode agar manusia dapat berkomunikasi dengan komputer serta tentunya mempermudah pekerjaan manusia. Terdapat beberapa perintah mudah yang diterapkan pada kelas hari ini. Seperti penjumlahan angka dan kata-kata. Contohnya sebagai berikut:
>>>a = 50
>>>b = 25
>>>a+b
75
Kelas diakhiri dengan pemberian tugas yang akan diselesaikan pada pertemuan selanjutnya dalam bentuk video. Untuk tugas yang diberikan kepada Mahasiswa adalah membuat aplikasi yang dapat mengukur top speed dari sebuah kendaraan.
Tugas 1
Kelompok:
1. Abraham Theodorus
2. Dimas Fahrul Rozi
3. Muhammad Ichsan
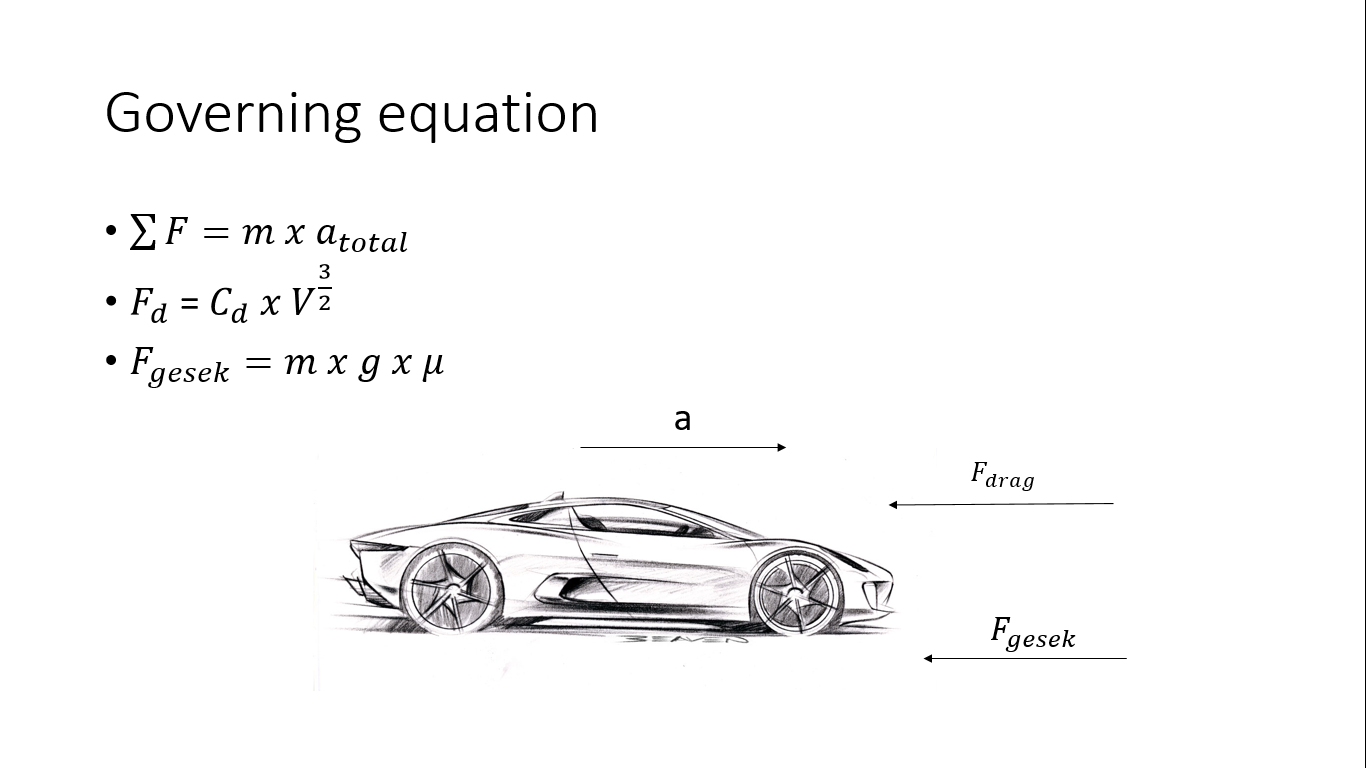
Berikut ini adalah governing equation dari mobil yang bergerak

 Pseudocode
Pseudocode
memasukkan nilai variabel yang diperlukan
g= float(9.8) #gravitational_acceleration
cd=eval(input("drag coefficient: "))
myu= float(input("koefisien gesek dinamis: "))
v0=eval(input("initial velocity (m/s): "))
m=eval(input("mass (kg): "))
a=eval(input("acceleration (m/s^2): "))
vt=eval(input("top speed (m/s): "))
semua dibagi m
fgesek=g*myu
fdrag=(cd*vt**(3/2))/m
ft=a
atot=ft-fdrag-fgesek
t=(vt-v0)/atot
print("waktu mobil untuk mencapai top speed: ",t, "detik")
Pertemuan 7 (5 november 2019)
Pada pertemuan kali ini, kita membahas tentang metode runge-kutta. Metode Runge Kutta adalah metode penyelesaian masalah nilai awal persamaan diferensial dengan pendekatan iterasi numerik. Metode Runge-Kutta adalah alternatif lain dari metode deret Taylor yang tidak membutuhkan perhitungan turunan. Metode ini berusaha mendapatkan derajat ketelitian yang lebih tinggi.