Difference between revisions of "Kelompok 2"
(→Tugas Besar) |
|||
| (19 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| + | 1. [[Ryanson Jonathan]] | ||
| + | |||
| + | 2. [[Agis Gilang Setiawan]] | ||
| + | |||
| + | 3. [[Ales Daniel]] | ||
| + | |||
| + | |||
===Eliminasi Gauss=== | ===Eliminasi Gauss=== | ||
<youtube width="200" height="100">Ysrz1P3X-_s</youtube> | <youtube width="200" height="100">Ysrz1P3X-_s</youtube> | ||
| Line 41: | Line 48: | ||
===Runge-Kutta Method=== | ===Runge-Kutta Method=== | ||
<youtube width="200" height="100">QfEgmJaGOAE</youtube> | <youtube width="200" height="100">QfEgmJaGOAE</youtube> | ||
| + | <youtube width="200" height="100">BMm8E_PxccE</youtube> | ||
| − | |||
Pengerjaan dilakukan dan kode dirancang untuk mengikuti contoh soal. | Pengerjaan dilakukan dan kode dirancang untuk mengikuti contoh soal. | ||
| Line 53: | Line 60: | ||
if 0 <= x < 2: | if 0 <= x < 2: | ||
# dydx menyatakan persamaan awal dalam soal. Persamaan harus diintegralkan sekali untuk menghasilkan persamaan kecepatan. | # dydx menyatakan persamaan awal dalam soal. Persamaan harus diintegralkan sekali untuk menghasilkan persamaan kecepatan. | ||
| − | # Didapat hasil | + | # Didapat hasil 2x^2 - 30xy karena dipakai massa m = 2,5 kg dan konstanta pegas k = 75 N/m. |
# P(t) dinyatakan dalam x. | # P(t) dinyatakan dalam x. | ||
def dydx(x, y): | def dydx(x, y): | ||
| Line 92: | Line 99: | ||
else: | else: | ||
print("Mohon masukkan nilai t positif.") | print("Mohon masukkan nilai t positif.") | ||
| + | |||
| + | [[File:Flowdiagram_RungeKutta_Kelompok2.jpg]] | ||
| + | |||
| + | ===CFD CAR DRAG ANALYSIS=== | ||
| + | |||
| + | Analysis drag dilakukan terlebih dahulu input data yang diperlukan pada ''CFD-Pre'' dan ''CFD-Solve''. Berikut adalah hasil setelah dilakukan ''Mesh Geometry'' dan ''Run Solver'' dari mobil yang akan dianalisa. | ||
| + | |||
| + | [[File:testcfdkel2_1.jpg|400px]] | ||
| + | |||
| + | Kemudian, pada bagian ''tab'' ''CFD-Post'', dilakukan running dengan aplikasi ''Paraview'' untuk mengetahui drag force yang ingin dicari tahu. | ||
| + | |||
| + | [[File:testcfdkel2_2.jpg|400px]] | ||
| + | |||
| + | Lalu, dilakukan pengerjaan dengan filter ''Generate Surface Normal'', dengan mengapply tampak car_body saja yang terlihat. Kemudian, dilakukan kalkulasi besar P terhadap gaya normal sumbu x. Hasil tersebut kemudian di apply kembali sehingga menghasilkan perhitungan yang diinginkan yaitu ''Drag Force'' yang ditentukan. Didapatkan besarnya setelah dilakukan ''filter'' dan integrasi perhitungan yang ada. Berikut adalah skema yang dilakukan: | ||
| + | |||
| + | [[File:testcfdkel2_3.jpg|400px]] | ||
| + | |||
| + | Kemudian, dilakukan percobaan lainnya dengan variasi V dengan interval 1 dari 10 hingga 20. Akhirnya, didapatkan data yang kemudian dibentuk grafiknya serta ''trendline'' yang berbentuk kurva sebagai berikut: | ||
| + | |||
| + | [[File:testcfdkel2_4.jpg|400px]] | ||
| + | |||
| + | |||
| + | ===Optimasi=== | ||
| + | Optimasi untuk kasus airfoil dilakukan menggunakan kode sbb: | ||
| + | |||
| + | # -*- coding: utf-8 -*- | ||
| + | """ | ||
| + | Created on Mon Dec 2 14:39:11 2019 | ||
| + | |||
| + | @author: rjsec | ||
| + | """ | ||
| + | |||
| + | import numpy as np | ||
| + | from scipy.optimize import minimize | ||
| + | |||
| + | |||
| + | def cdrag(x): | ||
| + | x1 = x[0] | ||
| + | drag = 0.0000003*x1**4-0.00002*x1**3+0.0008*x1**2+0.0026*x1-0.0517 | ||
| + | return drag | ||
| + | |||
| + | def clift(x): | ||
| + | x1 = x[0] | ||
| + | lift = 0.0000001*x1**4+0.00001*x1**3+0.0003*x1**2+0.0052*x1+0.0187 | ||
| + | return lift | ||
| + | |||
| + | def objective(x): | ||
| + | return cdrag(x) | ||
| + | |||
| + | def constraint1(x): | ||
| + | return 90 - cdrag(x) | ||
| + | def constraint2(x): | ||
| + | return 90 - clift(x) | ||
| + | |||
| + | con1=({'type':'ineq','fun':constraint1}) | ||
| + | con2=({'type':'ineq','fun':constraint2}) | ||
| + | cons = (con1,con2) | ||
| + | |||
| + | x1_guess = 50 | ||
| + | |||
| + | x0 = np.array([x1_guess]) | ||
| + | |||
| + | sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True}) | ||
| + | |||
| + | xopt = sol.x | ||
| + | forceopt = -sol.fun | ||
| + | |||
| + | dragopt = cdrag(xopt) | ||
| + | liftopt = clift(xopt) | ||
| + | |||
| + | print ("") | ||
| + | print ("Hasil optimasi:") | ||
| + | print ("Sudut optimal = "+str(-xopt[0])) | ||
| + | print ("Total force optimal = "+str(forceopt)) | ||
| + | print ("Drag force optimal = "+str(-dragopt)) | ||
| + | print ("Lift force optimal = "+str(liftopt)) | ||
| + | |||
| + | |||
| + | == Tugas Besar == | ||
| + | '''Spesifikasi Airfoil''' | ||
| + | [[File:TB1.png]] | ||
| + | Airfoil yang digunakan adalah MH 70 11.08% - Martin Hepperle MH70 | ||
| + | Span = 2 mm | ||
| + | Root and Tip Chord = 10 mm | ||
| + | |||
| + | '''Pembuatan model airfoil''' | ||
| + | Airfoil dibuat dengan menggunakan software Autodesk Inventor | ||
| + | [[File:TB2.png]] | ||
| + | |||
| + | '''Simulasi menggunakan CFD''' | ||
| + | Model yang sudah dibuat diimport ke CFDSOF | ||
| + | [[File:TB3.png]] | ||
| + | Model memasuki tahap ''meshing'' | ||
| + | |||
| + | Berikut adalah ''Boundary geometry'' untuk proses ''meshing'' | ||
| + | [[File:TB4.png]] | ||
| + | |||
| + | Model memasuki tahap-tahap analisis sebagai berikut | ||
| + | [[File:TB5.png]] | ||
| + | |||
| + | [[File:TB6.png]] | ||
| + | |||
| + | [[File:TB7.png]] | ||
| + | |||
| + | [[File:TB8.png]] | ||
| + | |||
| + | [[File:TB9.png]] | ||
| + | |||
| + | [[File:TB10.png]] | ||
| + | |||
| + | [[File:TB11.png]] | ||
| + | |||
| + | [[File:TB12.png]] | ||
| + | |||
| + | '''Perhitungan menggunakan Paraview''' | ||
| + | Model ''meshing'' diimport ke Paraview | ||
| + | Perhitungan dilakukan dengan tahap berikut | ||
| + | [[File:TB12.png]] | ||
| + | |||
| + | [[File:TB13.png]] | ||
| + | |||
| + | [[File:TB14.png]] | ||
| + | |||
| + | [[File:TB15.png]] | ||
| + | |||
| + | [[File:TB16.png]] | ||
| + | |||
| + | [[File:TB17.png]] | ||
| + | |||
| + | [[File:TB18.png]] | ||
| + | |||
| + | '''Hasil Percobaan''' | ||
| + | ''Data Percobaan'' | ||
| + | Data Percobaan | ||
| + | [[File:TB19.png]] | ||
| + | |||
| + | ''Grafik Percobaan'' | ||
| + | Berikut adalah grafik lift dan drag kami | ||
| + | [[File:TB20.png]] | ||
| + | |||
| + | ''Optimasi'' | ||
| + | Kode yang digunakan | ||
| + | [[File:TB21.png]] | ||
| + | |||
| + | Berikut hasil optimasi yang dilakukan | ||
| + | [[File:TB22.png]] | ||
| + | |||
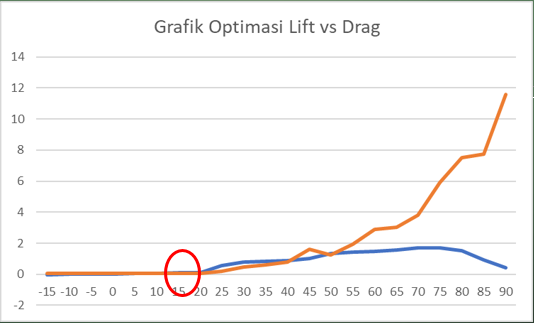
| + | Grafik hasil optimasi Lift vs Drag | ||
| + | |||
| + | [[File:TB23.png]] | ||
Latest revision as of 17:50, 8 December 2019
3. Ales Daniel
Eliminasi Gauss
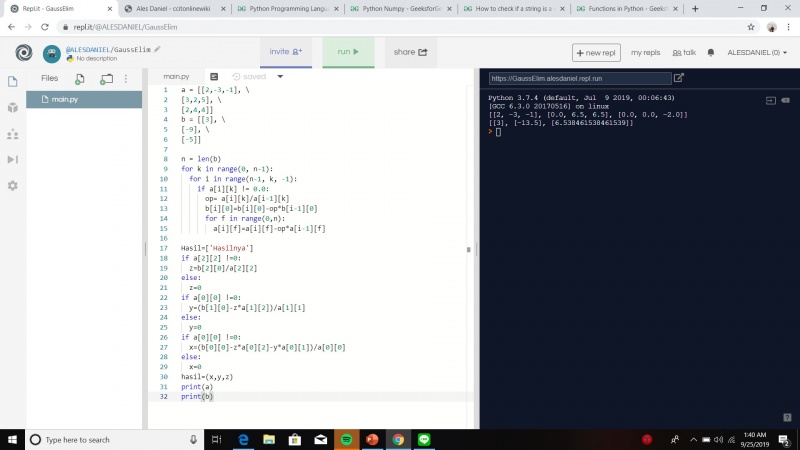
Pengerjaan dilakukan menggunakan algoritma Gauss seperti yang ada di buku Phyton. Namun, yang membedakan adalah tidak menggunakan module pada pengerjaan ini. Berikut adalah algoritma yang sudah dirancang berdasarkan soal pada buku Phyton :
Algoritma yang kami gunakan adalah sebagai berikut:
a = [[2,-3,-1], \
[3,2,5], \
[2,4,4]]
b = [[3], \
[-9], \
[-5]]
n = len(b)
for k in range(0, n-1):
for i in range(n-1, k, -1):
if a[i][k] != 0.0:
op= a[i][k]/a[i-1][k]
b[i][0]=b[i][0]-op*b[i-1][0]
for f in range(0,n):
a[i][f]=a[i][f]-op*a[i-1][f]
Hasil=['Hasilnya']
if a[2][2] !=0:
z=b[2][0]/a[2][2]
else:
z=0
if a[0][0] !=0:
y=(b[1][0]-z*a[1][2])/a[1][1]
else:
y=0
if a[0][0] !=0:
x=(b[0][0]-z*a[0][2]-y*a[0][1])/a[0][0]
else:
x=0
hasil=(x,y,z)
print(a)
Runge-Kutta Method
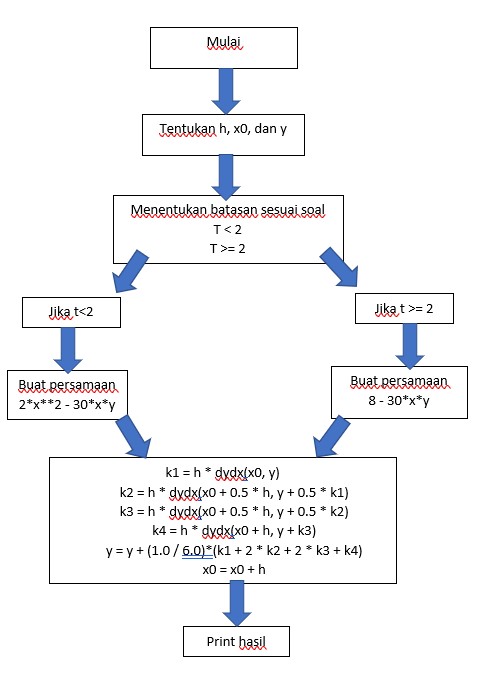
Pengerjaan dilakukan dan kode dirancang untuk mengikuti contoh soal.
# Di sini, kita akan menggunakan x0 dan y sebagai titik asal, x sebagai t yang diinginkan, dan h sebagai increment. Kita menggunakan h = 0.01.
x0 = 0
y = 0
h = 0.01
x = float(input("Masukkan nilai t: "))
if 0 <= x < 2:
# dydx menyatakan persamaan awal dalam soal. Persamaan harus diintegralkan sekali untuk menghasilkan persamaan kecepatan.
# Didapat hasil 2x^2 - 30xy karena dipakai massa m = 2,5 kg dan konstanta pegas k = 75 N/m.
# P(t) dinyatakan dalam x.
def dydx(x, y):
return (2*x**2 - 30*x*y)
# Ini merupakan implementasi perhitungan Runge-Kutta.
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
# untuk y selanjutnya
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# untuk x selanjutnya
x0 = x0 + h
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
elif x >= 2:
# Ketika x >= 2, perhitungan harus diganti karena P(t) sudah konstan di angka 20 N.
def dydx(x, y):
return (8 - 30*x*y)
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
x0 = x0 + h
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
else:
print("Mohon masukkan nilai t positif.")
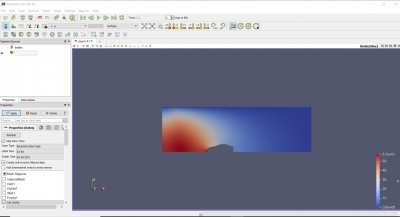
CFD CAR DRAG ANALYSIS
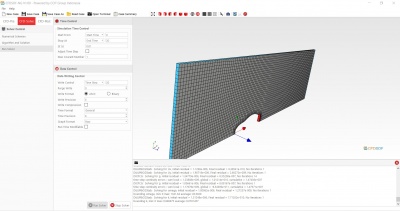
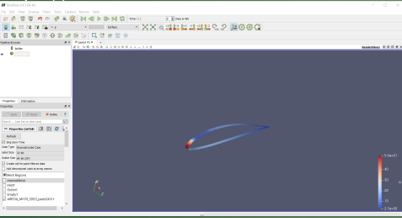
Analysis drag dilakukan terlebih dahulu input data yang diperlukan pada CFD-Pre dan CFD-Solve. Berikut adalah hasil setelah dilakukan Mesh Geometry dan Run Solver dari mobil yang akan dianalisa.
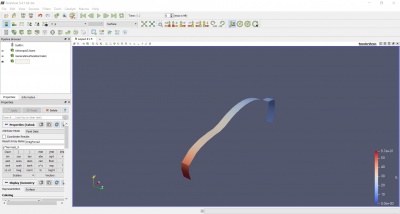
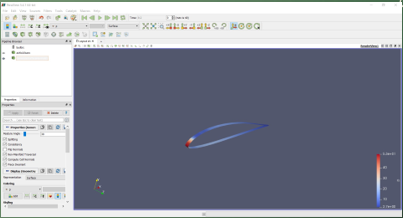
Kemudian, pada bagian tab CFD-Post, dilakukan running dengan aplikasi Paraview untuk mengetahui drag force yang ingin dicari tahu.
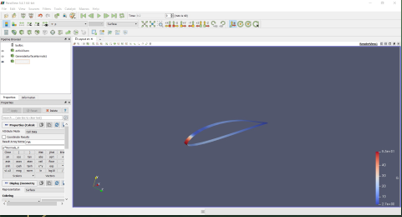
Lalu, dilakukan pengerjaan dengan filter Generate Surface Normal, dengan mengapply tampak car_body saja yang terlihat. Kemudian, dilakukan kalkulasi besar P terhadap gaya normal sumbu x. Hasil tersebut kemudian di apply kembali sehingga menghasilkan perhitungan yang diinginkan yaitu Drag Force yang ditentukan. Didapatkan besarnya setelah dilakukan filter dan integrasi perhitungan yang ada. Berikut adalah skema yang dilakukan:
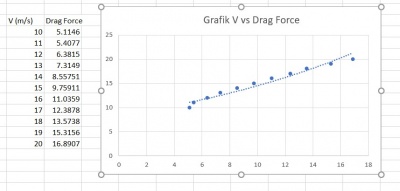
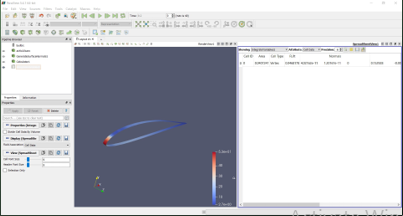
Kemudian, dilakukan percobaan lainnya dengan variasi V dengan interval 1 dari 10 hingga 20. Akhirnya, didapatkan data yang kemudian dibentuk grafiknya serta trendline yang berbentuk kurva sebagai berikut:
Optimasi
Optimasi untuk kasus airfoil dilakukan menggunakan kode sbb:
# -*- coding: utf-8 -*-
"""
Created on Mon Dec 2 14:39:11 2019
@author: rjsec
"""
import numpy as np
from scipy.optimize import minimize
def cdrag(x):
x1 = x[0]
drag = 0.0000003*x1**4-0.00002*x1**3+0.0008*x1**2+0.0026*x1-0.0517
return drag
def clift(x):
x1 = x[0]
lift = 0.0000001*x1**4+0.00001*x1**3+0.0003*x1**2+0.0052*x1+0.0187
return lift
def objective(x):
return cdrag(x)
def constraint1(x):
return 90 - cdrag(x)
def constraint2(x):
return 90 - clift(x)
con1=({'type':'ineq','fun':constraint1})
con2=({'type':'ineq','fun':constraint2})
cons = (con1,con2)
x1_guess = 50
x0 = np.array([x1_guess])
sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True})
xopt = sol.x
forceopt = -sol.fun
dragopt = cdrag(xopt)
liftopt = clift(xopt)
print ("")
print ("Hasil optimasi:")
print ("Sudut optimal = "+str(-xopt[0]))
print ("Total force optimal = "+str(forceopt))
print ("Drag force optimal = "+str(-dragopt))
print ("Lift force optimal = "+str(liftopt))
Tugas Besar
Spesifikasi AirfoilAirfoil yang digunakan adalah MH 70 11.08% - Martin Hepperle MH70 Span = 2 mm Root and Tip Chord = 10 mm
Pembuatan model airfoil Airfoil dibuat dengan menggunakan software Autodesk Inventor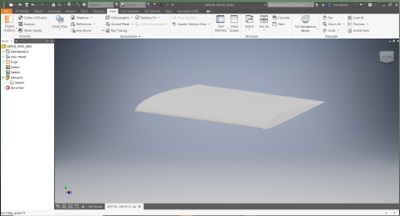
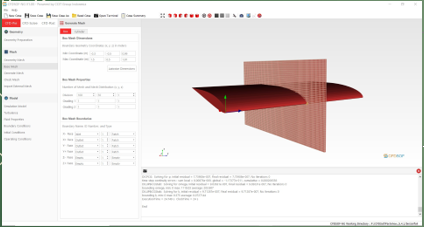
Simulasi menggunakan CFD Model yang sudah dibuat diimport ke CFDSOFModel memasuki tahap meshing Berikut adalah Boundary geometry untuk proses meshing
Model memasuki tahap-tahap analisis sebagai berikut
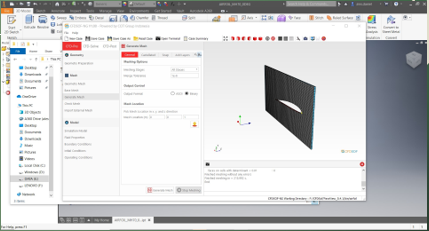
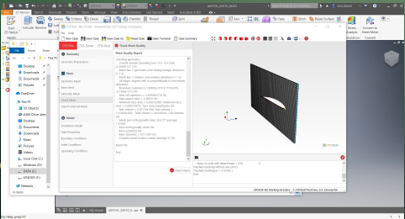
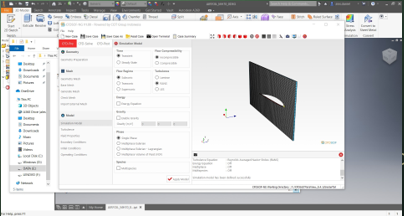
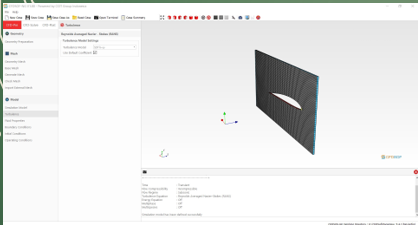
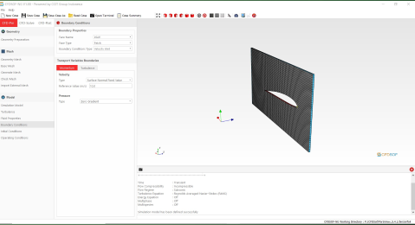
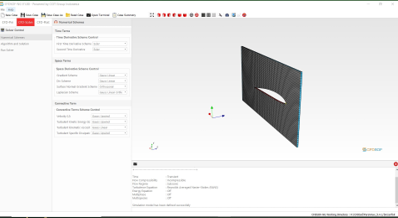
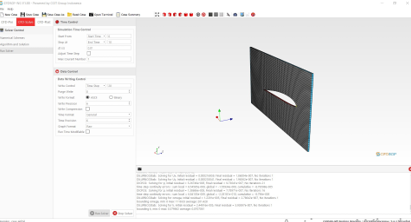
Perhitungan menggunakan Paraview Model meshing diimport ke Paraview Perhitungan dilakukan dengan tahap berikut
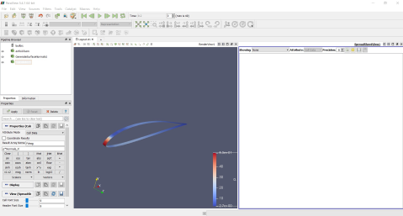
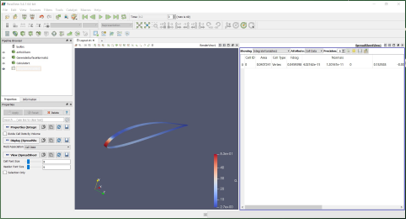
Hasil Percobaan Data Percobaan Data PercobaanGrafik Percobaan Berikut adalah grafik lift dan drag kami
Optimasi Kode yang digunakan
Berikut hasil optimasi yang dilakukan
Grafik hasil optimasi Lift vs Drag