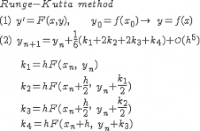Difference between revisions of "Kelompok 13"
(→TUBES NO. 3 Analisis Pengaruh Sudut Serang pada Airfoil) |
(→TUBES NO. 3 Analisis Pengaruh Sudut Serang pada Airfoil) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 233: | Line 233: | ||
Airfoil merupakan profil dari sebuah sayap yang terdapat pada sayap pesawat ataupun wahana lain dengan tujuan untuk mendapatkan gaya angkat atau gaya tekan bergantung dari profilnya itu sendiri. Untuk sebuah pesawat, fungsi airfoil adalah untuk mendapatkan lift atau gaya angkat agar pesawat dapat | Airfoil merupakan profil dari sebuah sayap yang terdapat pada sayap pesawat ataupun wahana lain dengan tujuan untuk mendapatkan gaya angkat atau gaya tekan bergantung dari profilnya itu sendiri. Untuk sebuah pesawat, fungsi airfoil adalah untuk mendapatkan lift atau gaya angkat agar pesawat dapat | ||
| − | terbang. Airfoil yang kami gunakan dalam proses analisis ini menggunakan airfoil dari internet dengan nama NH-70. Berikut ini adalah bentuk profil NH-70 beserta proses analisisnya. | + | terbang. Airfoil yang kami gunakan dalam proses analisis ini menggunakan airfoil dari internet dengan nama NH-70. Airfoil dianalisis dengan kecepatan inlet sebesar 50 m/s. Analisis dilakukan untuk mencari besar drag dan lift yang terbentuk dengan variari sudut serang (''Angle of Attack'') tiap 15 derajat dari -15 sampai 90 derajat. Berikut ini adalah bentuk profil NH-70 beserta proses analisisnya. |
[[File:nh7013.JPG|700px|center]] | [[File:nh7013.JPG|700px|center]] | ||
| Line 245: | Line 245: | ||
[[File:drag9013.png|700px|center]] | [[File:drag9013.png|700px|center]] | ||
| − | [[File: | + | Dari proses analisis diatas, maka didapatkan hasil berupa data besar sudut serang, data drag, dan data lift. Berikut ini adalah grafik Drag vs Sudut serang, Lift vs Sudut serang, dan Lift/Drang vs Sudut serang. Grafik Lift/Drag diperlukan karena banyak proses pencarian airfoil yang membutuhkan data tersebut yang menggambarkan secara jelas performa airfoil pada setiap derajatnya. |
| + | |||
| + | [[File:dataliftdrag13.JPG|500px|center]] | ||
| + | |||
| + | [[File:Dragairfoil13.JPG|700px|center]] | ||
| + | |||
| + | [[File:liftairfoil13.JPG|700px|center]] | ||
| + | |||
| + | [[File:liftdragairfoil13.JPG|700px|center]] | ||
| + | |||
| + | |||
| + | Dari semua data di atas, dilakukan analisis optimasi untuk mencari pada sudut mana airfoil ini sangat optimum. | ||
| + | |||
| + | import numpy as np | ||
| + | from scipy.optimize import minimize | ||
| + | def calc_drag(x):#drag | ||
| + | x1 = x[0] | ||
| + | drag = 0.0017*x1**3-0.0516*x1**2-0.6403*x1+10.537 | ||
| + | return drag | ||
| + | def calc_lift(x): #lift | ||
| + | x1 = x[0] | ||
| + | lift = -0.0005*x1**3+0.0568*x1**2-0.2805*x1-14.462 | ||
| + | return lift | ||
| + | def objective(x): #volume yang diminimalkan | ||
| + | return calc_lift(x) | ||
| + | def constraint1(x): #variable SUDUT yang meminimalkan persamaan garis drag | ||
| + | return 90 - calc_drag(x) | ||
| + | def constraint2(x): #variable SUDUT yang meminimalkan persamaan garis lift | ||
| + | return 90 - calc_lift(x) | ||
| + | con1=({'type':'ineq','fun':constraint1}) | ||
| + | con2=({'type':'ineq','fun':constraint2}) | ||
| + | cons = (con1,con2) | ||
| + | x1_guess = 50 | ||
| + | x0 = np.array([x1_guess]) | ||
| + | sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True}) | ||
| + | xopt = sol.x | ||
| + | forceopt = -sol.fun | ||
| + | dragopt = calc_drag(xopt) # drag optimal | ||
| + | liftopt = calc_lift(xopt) # lift optimal | ||
| + | print ('sudut optimal = '+str(xopt[0])) | ||
| + | print ('total force optimal = '+str(-forceopt)) | ||
| + | print ('drag force optimal = '+str(dragopt)) | ||
| + | print ('lift force optimal = '+str(liftopt)) | ||
| + | |||
| + | Berikut ini adalah hasil running dengan kode python diatas: | ||
| + | |||
| + | [[File:Optimasiairfoil13.JPG|600px|center]] | ||
| + | |||
| + | Dengan demikian, maka sudut yang paling optimum pada airfoil ini adalah pada 2 derajat. | ||
Latest revision as of 13:54, 4 December 2019
Anggota Kelompok 13:
1. Viliasio Sirait
2. Muhammad Luqman Sugiyono
3. Zaim Kamil Muhammad
Contents
Pada pertemuan keempat, kami ditantang untuk membuat sebuah program python yang mampu menjawab eliminasi Gauss dari sebuh matriks. Eliminasi Gauss adalah suatu cara mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks yang lebih sederhana. Caranya adalah dengan melakukan operasi baris sehingga matriks tersebut menjadi matriks yang eselon-baris. Ini dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan menggunakan matriks. Caranya dengan mengubah persamaan linear tersebut ke dalam matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks Eselon-baris, lakukan substitusi balik untuk mendapatkan nilai dari variabel-variabel tersebut.
Eliminasi Gauss ini disempurnakan kembali dengan yang namanya Eliminasi Gauss Jordan. Dalam aljabar linear, eliminasi Gauss-Jordan adalah versi dari eliminasi Gauss. Pada metode eliminasi Gauss-Jordan kita membuat nol elemen-elemen di bawah maupun di atas diagonal utama suatu matriks. Hasilnya adalah matriks tereduksi yang berupa matriks diagonal satuan (semua elemen pada diagonal utama bernilai 1, elemen-elemen lainnya nol).
Berikut ini adalah kode program python yang telah saya pelajari:
from fractions import Fraction
def pprint(A):
n = len(A)
for i in range(0, n):
line = ""
for j in range(0, n+1):
line += str(A[i][j]) + "\t"
if j == n-1:
line += "| "
print(line)
print("")
# Performs and returns the gauss elimination
# @A : matrix
def gauss(A):
n = len(A)
for i in range(0, n):
# Search for maximum in this column
maxE1 = abs(A[i][i])
maxRow = i
for k in range(i+1, n):
# compares rows, first row can't start with zero
if abs(A[k][i]) < maxE1 or maxE1 == 0:
maxE1 = abs(A[k][i])
maxRow = k
# Swap maximum row with current row (column by column)
for k in range(i, n+1):
tmp = A[maxRow][k]
A[maxRow][k] = A[i][k]
A[i][k] = tmp
# Make all rows below this one 0 in current column
for k in range(i+1, n):
c = -A[k][i]/A[i][i]
for j in range(i, n+1):
if i == j:
A[k][j] = 0
else:
A[k][j] += c * A[i][j]
# Print echelon matrix
print("Echelon Matrix:\t")
pprint(A)
# Solve equation Ax = b for echelon matrix
x = [0 for i in range(n)]
for i in range(n - 1, -1, -1):
# there is no solution
if A[i][i] == 0:
return [0 for i in range(n)]
# normal solution
else:
x[i] = A[i][n]/A[i][i]
for k in range(i-1, -1, -1):
A[k][n] -= A[k][i]*x[i]
return x
# test code
print('Please input the number of variables:')
n = int(input())
# creates a matrix of zeros
A = [[0 for j in range(n+1)] for i in range(n)]
# Read input data
print("Please enter each row separated by a new line:")
for i in range(0, n):
line = map(Fraction, input().split(" "))
for j, el in enumerate(line):
A[i][j] = el
print("Please enter the solution column with values separated by spaces:")
line = input().split(" ")
lastLine = list(map(Fraction, line))
for i in range(0, n):
A[i][n] = lastLine[i]
# Print input
print("\nMatrix:")
pprint(A)
# Calculate solution
x = gauss(A)
# Print solution
print("Result:")
# check results
solution = False
for i in range(n):
if x[i] != 0:
solution = True
# a solution exists
if solution:
for i in range(len(x)):
print("x", i+1, " = ", x[i])
# a solution does not exist
else:
print("No Solution")
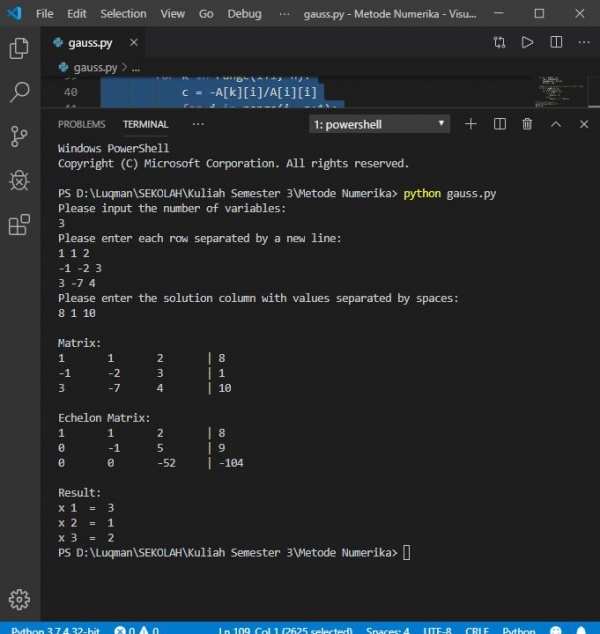
Ketika kode python ini dijalankan, maka akan keluar instruksi untuk mnginput banyak variabel dari sistem persamaan liniar. Setelah menginput variabel, muncul juga instruksi untuk memasukkan isi dari vektor variabel. Berikut ini merupakan sebuah contoh dari penggunaan kode python ini:
Ketika dibandingkan dengan kalkulator eliminasi gauss, didapatkan hasil yang benar-benar sama.
Aplikasi Runge Kutta
2. Algoritma penyelesaian persamaan diferensial dengan Runge Kutta
a. Terdapat sebuah pegas dengan dengan k = 75 N/m, dikaitkan dengan massa sebesar 2.5 kg
b. Massa ditarik dengan fungsi P(t)
c. Jika massa ditarik dalam waktu kurang dari 2 detik, maka gaya yang menarik massa adalah 10t.
d. jika massa ditarik dalam 2 detik atau lebih, maka gaya yang menarik massa adalah 20 N.
e. Regangan terjauh ditentukan oleh besaran gaya yang menarik massa.
f. regangan terjauh dirumuskan dengan metode Runge Kutta, dengan y" terjauh = P(t)/m - ky/m
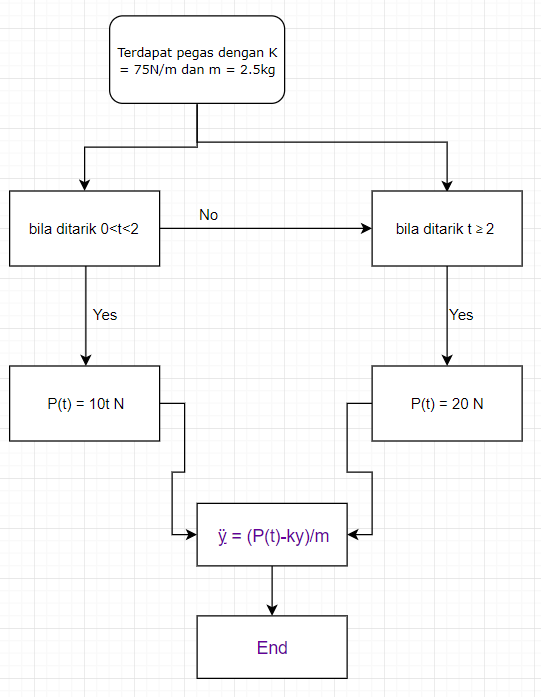
3. Membuat Flow Chart
4. Program Pyhton dengan Penyelesaian Aplikasi Runge Kutta
x0 = 0 # perpindahan ke-0 adalah 0
y = 0
h = 0.01 # step size sebesar 0.01
t = float(input("Masukkan nilai t: "))
if 0 <= t < 2:
# dydx menyatakan persamaan awal dalam soal.
# Didapat hasil 4x - 30y karena dipakai massa m = 2,5 kg dan konstanta pegas k = 75 N/m.
# P(t) dinyatakan dalam x.
def dydx(x, y):
return (4*x - 30*y)
# Ini merupakan implementasi perhitungan Runge-Kutta.
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
# untuk y selanjutnya
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# untuk x selanjutnya
x0 = x0 + h
return y
print("Nilai y pada t =", t, "adalah", rungeKutta(x0, y, t, h))
elif t >= 2:
# Ketika x >= 2, maka variabel x sudah tidak lagi memengaruhi persamaan.
def dydx(x, y):
return (8 - 30*y)
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
x0 = x0 + h
return y
print("Nilai y pada t =", t, "adalah", rungeKutta(x0, y, t, h))
else:
print("Mohon masukkan nilai t positif.")
TUBES NO. 2 Analisis Drag Force pada Mobil Bergerak
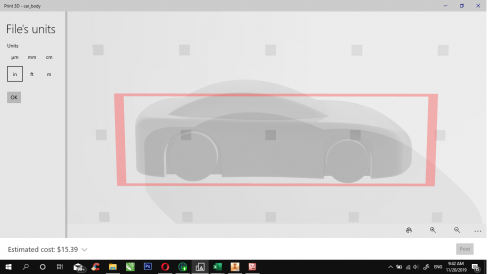
Analisis untuk mendapatkan drag force pada mobil yang bergerak dilakukan pada aplikasi CFDSOF dan dilanjutkan pada ParaView. Untuk melakukan analisis, harus tersedia dulu model dari mobil tersebut dan dibuat dengan geometri tertentu. Pembuatan mobil di Inventor tidak bisa dengan ukuran sebesar mobil nyata karena akan terjadi error saat melakukan analisis di CFD. Pada tugas nomer 2 ini, kami diminta untuk mencari drag force pada mobil yang telah disediakan oleh asdos. Dalam proses pencarian drag, kecepatan velocity inlet dibuat sebagai variabel terikat (divariasikan). Tentu saja setelah velocuty inlet divariasikan, akan mendapatkan drag force yang beragam. Kemudian data-data kecepatan-drag force ini dibuat dalam kurva dan dibuat garis trendline nya di excel. Berikut ini adalah hasil yang telah kami lakukan pada analisis drag force dari mobil yang diberikan oleh asdos:
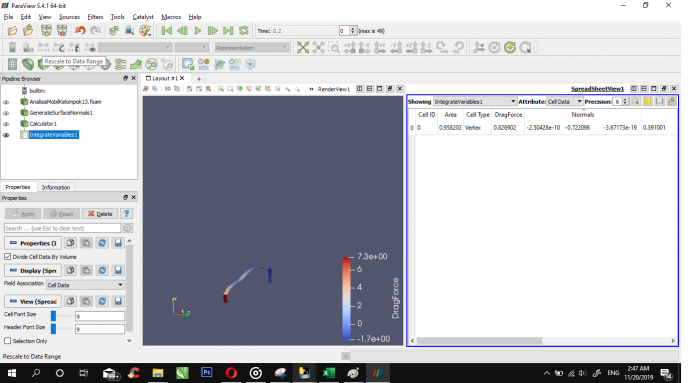
Gambar diatas merupakan tampak mobil yang akan dianalisa kali ini. dengan bentuk sedemikian rupa, didapatkan area yang menyebabkan DragForce sebesar 0.958202 m^2.
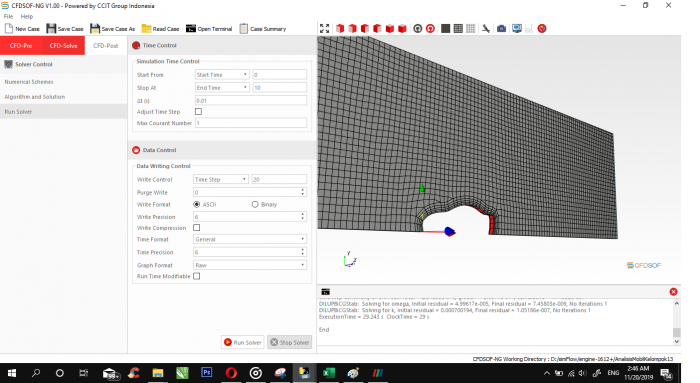
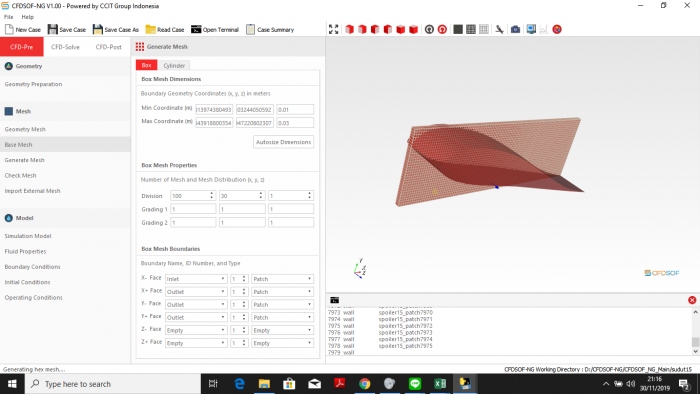
Proses Analisis Mobil pada software CFDSOF.
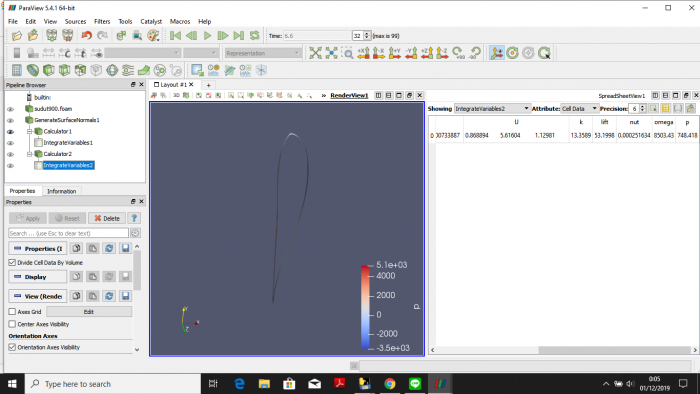
Proses Analisis Mobil pada software Paraview.
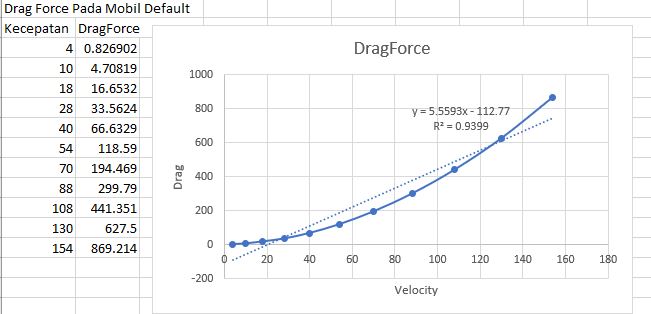
Hasil data-data kecepatan dan drag force yang telah ditemukan. Dibuat grafik v vs Drag dan dibuat regresi linearnya.
TUBES NO. 3 Analisis Pengaruh Spoiler pada Drag Force yang Terjadi Pada Mobil Bergerak
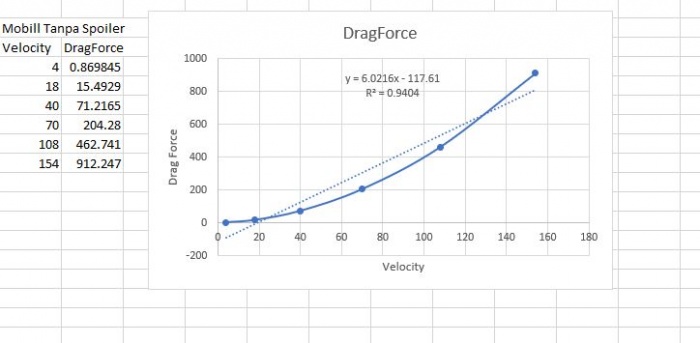
Tugas besar nomor 3 ini mahasiswa diminta untuk membuat sebuah mobil rancangan sendiri yang nantinya akan dianalisis drag forcenya sama seperti nomor 2. Yang membedakan disini adalah pada analisis mobil yang kita desain harus terdapat spoiler yang berfungsi membuat downforce. Disini akan terdapat banyak sekali data, karena terdapat variasi sudut spoiler relatif terhadap mobil dan terdapat variasi kecepatan di tiap variasi spoiler tersebut. Pertama-tama kami memulai analisis dengan mobilnya saja tanpa menggunakan spoiler. Berikut ini hasil yang kami dapatkan dari analisis tersebut.
Gambaran mobil tanpa spoiler yang kami gunakan dalam analisis ini.
Gambar hasil analisa kami.
Lalu setelah membuat mobil tanpa spoiler, kami membuat mobil dengan spoiler yang tentu saja bukan spoiler yang rumit. Berikut ini adalah gambar mobil sudah dilengkapi dengan spoiler.
Namun sayangnya, proses analisa nobil dengan spoiler ini terpaksa untuk dihentikan karena objek yang akan dianalisis dinilai terlalu sulit dan objek analisis diganti menjadi sebuah airfoil yang akan kami kerjaan di nomor selanjutnya.
TUBES NO. 3 Analisis Pengaruh Sudut Serang pada Airfoil
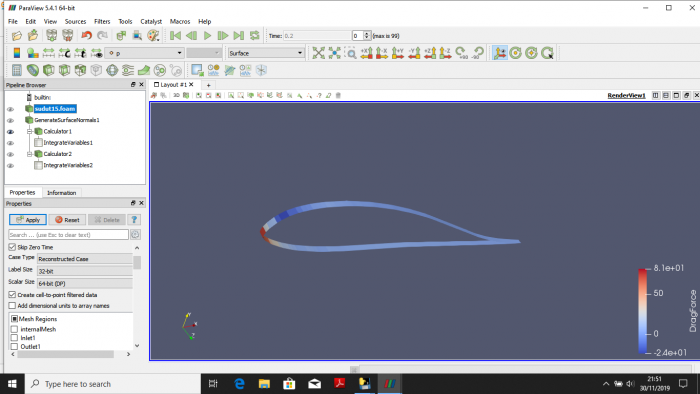
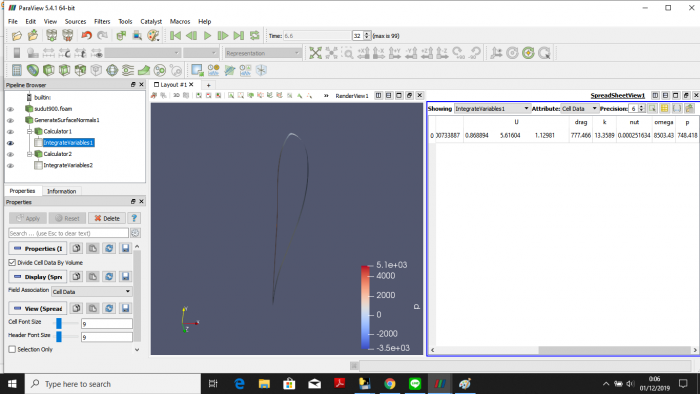
Airfoil merupakan profil dari sebuah sayap yang terdapat pada sayap pesawat ataupun wahana lain dengan tujuan untuk mendapatkan gaya angkat atau gaya tekan bergantung dari profilnya itu sendiri. Untuk sebuah pesawat, fungsi airfoil adalah untuk mendapatkan lift atau gaya angkat agar pesawat dapat terbang. Airfoil yang kami gunakan dalam proses analisis ini menggunakan airfoil dari internet dengan nama NH-70. Airfoil dianalisis dengan kecepatan inlet sebesar 50 m/s. Analisis dilakukan untuk mencari besar drag dan lift yang terbentuk dengan variari sudut serang (Angle of Attack) tiap 15 derajat dari -15 sampai 90 derajat. Berikut ini adalah bentuk profil NH-70 beserta proses analisisnya.
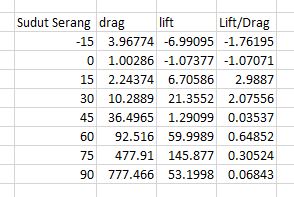
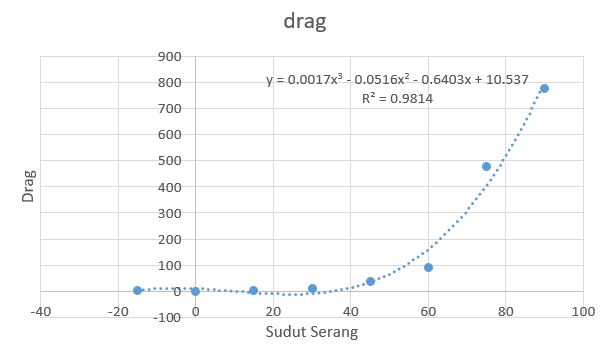
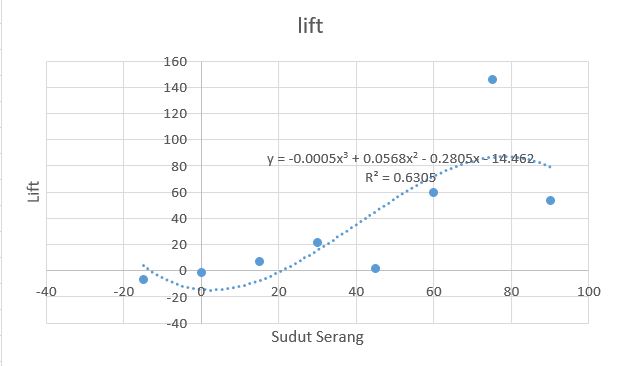
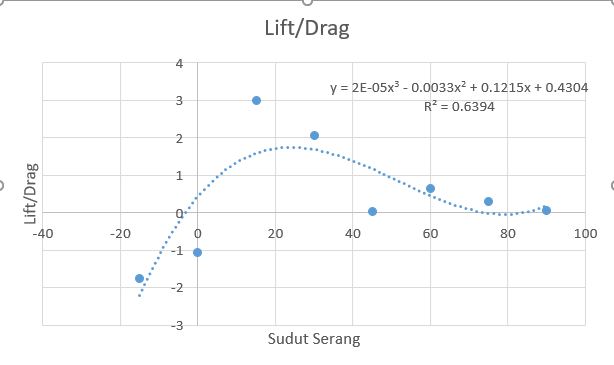
Dari proses analisis diatas, maka didapatkan hasil berupa data besar sudut serang, data drag, dan data lift. Berikut ini adalah grafik Drag vs Sudut serang, Lift vs Sudut serang, dan Lift/Drang vs Sudut serang. Grafik Lift/Drag diperlukan karena banyak proses pencarian airfoil yang membutuhkan data tersebut yang menggambarkan secara jelas performa airfoil pada setiap derajatnya.
Dari semua data di atas, dilakukan analisis optimasi untuk mencari pada sudut mana airfoil ini sangat optimum.
import numpy as np
from scipy.optimize import minimize
def calc_drag(x):#drag
x1 = x[0]
drag = 0.0017*x1**3-0.0516*x1**2-0.6403*x1+10.537
return drag
def calc_lift(x): #lift
x1 = x[0]
lift = -0.0005*x1**3+0.0568*x1**2-0.2805*x1-14.462
return lift
def objective(x): #volume yang diminimalkan
return calc_lift(x)
def constraint1(x): #variable SUDUT yang meminimalkan persamaan garis drag
return 90 - calc_drag(x)
def constraint2(x): #variable SUDUT yang meminimalkan persamaan garis lift
return 90 - calc_lift(x)
con1=({'type':'ineq','fun':constraint1})
con2=({'type':'ineq','fun':constraint2})
cons = (con1,con2)
x1_guess = 50
x0 = np.array([x1_guess])
sol = minimize(objective,x0, method='SLSQP',constraints=cons, options={'disp':True})
xopt = sol.x
forceopt = -sol.fun
dragopt = calc_drag(xopt) # drag optimal
liftopt = calc_lift(xopt) # lift optimal
print ('sudut optimal = '+str(xopt[0]))
print ('total force optimal = '+str(-forceopt))
print ('drag force optimal = '+str(dragopt))
print ('lift force optimal = '+str(liftopt))
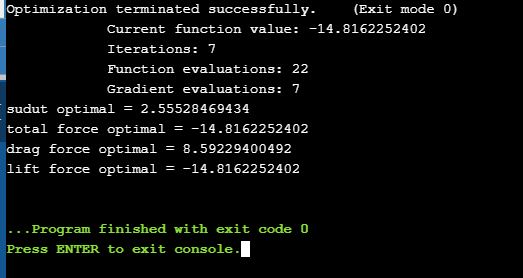
Berikut ini adalah hasil running dengan kode python diatas:
Dengan demikian, maka sudut yang paling optimum pada airfoil ini adalah pada 2 derajat.