Difference between revisions of "PYTHON - Kelas Metode Numerik"
| (13 intermediate revisions by the same user not shown) | |||
| Line 78: | Line 78: | ||
[[File:Eliminasi Gauss Part 1.mp4]] | [[File:Eliminasi Gauss Part 1.mp4]] | ||
| − | + | [[File:Eliminasi Gauss Part 2.mp4]] | |
| − | + | [[File:Eliminasi Gauss Part 3.mp4]] | |
| − | + | [[File:Eliminasi Gauss part 4.mp4]] | |
| − | + | [[File:Eliminasi Gauss part 5.mp4]] | |
| Line 94: | Line 94: | ||
Sistem pegas seri dapat ditinjau melalu metode finite elemenet analysis (FEA). Dengan FEA, pegas ditinjau pada setiap elemen dengan setiap node yang ada pada masing-masing elemen pegas. Eliminasi Gauss, dengan menggunakan program Python juga dapat digunakan untuk menyelesaikan sistem pegas seri yang ditinjau dengan metode FEA. Tutorial dan penjelasan singkat mengenai penyelesaian sistem pegas seri dengan menggunakan python dapat dilihat pada video berikut: | Sistem pegas seri dapat ditinjau melalu metode finite elemenet analysis (FEA). Dengan FEA, pegas ditinjau pada setiap elemen dengan setiap node yang ada pada masing-masing elemen pegas. Eliminasi Gauss, dengan menggunakan program Python juga dapat digunakan untuk menyelesaikan sistem pegas seri yang ditinjau dengan metode FEA. Tutorial dan penjelasan singkat mengenai penyelesaian sistem pegas seri dengan menggunakan python dapat dilihat pada video berikut: | ||
| − | + | [[File:Pegas Seri part 1.mp4]] | |
| − | + | [[File:Pegas Seri part 2.mp4]] | |
| − | + | [[File:Pegas Seri part 3.mp4]] | |
| − | + | [[File:Pegas Seri part 4.mp4]] | |
| − | + | [[File:Pegas Seri part 5.mp4]] | |
| + | |||
| + | ==Metode Numerik untuk persamaan diferrensial-Runge-Kutta== | ||
| + | |||
| + | Metode Numerik juga dapat digunakan untuk menyelesaikan persaan diferrensial biasa (Oder Differential Equation) atau yang dikenal dengan ODE. Penggunakan metode numerik untuk menyelesaikan ODE didasarkan pada beberapa hal sebagai berikut: | ||
| + | 1.Metode numerik dapat menyelesaikan persaaman differensial biasa secara effektif dan lebih mudah dibandingkan dengan penyelesain secara exact. | ||
| + | |||
| + | 2.Terdapat banyak kasus dimana persamaan diferensial biasa tidak bisa diselesaikan secara exact, namun bisa diselesaikan secara numerikal. | ||
| + | |||
| + | 3.Pada aplikasinya, sebagian besar persoalan mengenai persamaan differensial biasa diselesaikan menggunakan metode numerik, khususnya di era komputerisasi. | ||
| + | Untuk menyelesaikan persamaan differensial biasa secara numerikal, ada beberapa metode yang dapat digunakan, diantaranya adalah metode runge-kutta. Secara mendasar, pendekatan dengan menggunakan metode runge-kutta dapat digambarkan sebgai berikut: | ||
| + | |||
| + | [[File:runge-kutta1.JPG]] | ||
| + | |||
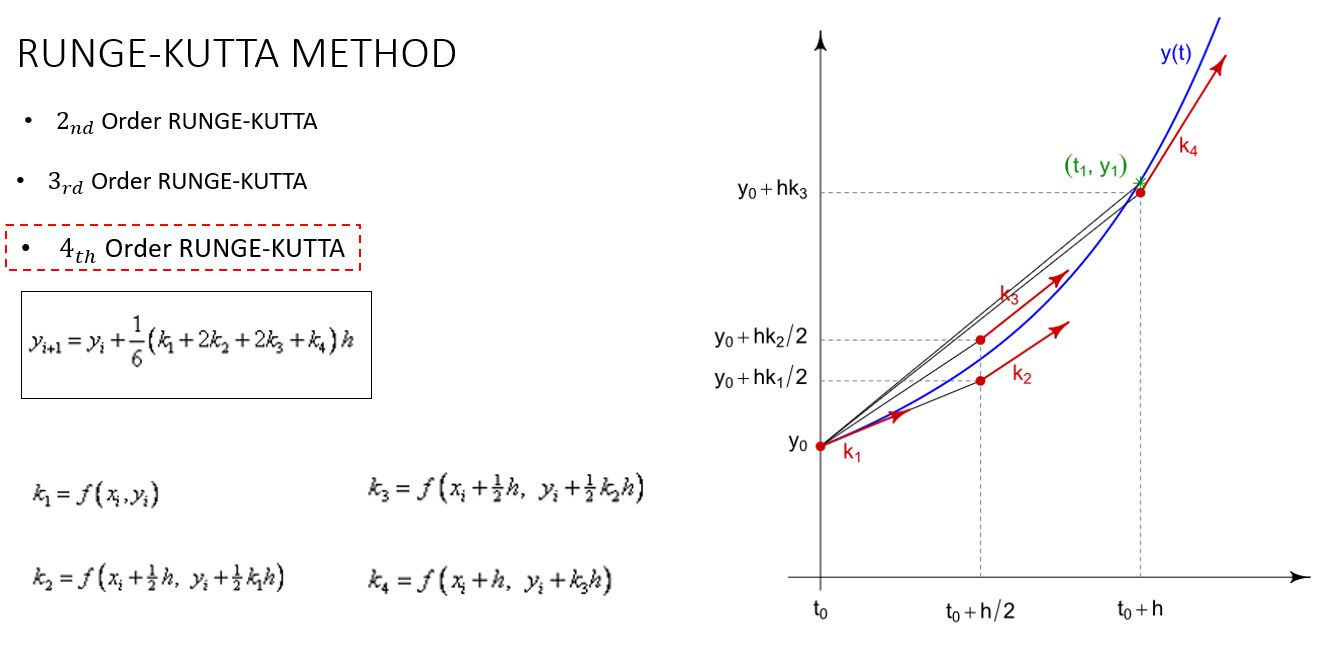
| + | Metode Runge-Kutta terdiri dari beberapa orde, dimuluai dari metode Runge-Kutta orde 2, yaitu metode Rungge-Kutta yang paling sederhana. Metode Rungge-Kutta orde 3 dapat menghasilkan akurasi yang lebih baik. Begitu juga dengan metode Rungge-Kutta orde 4 dapat menghasilkan hasil pendekatan dengan akurasi yang lebih baik dari pada metode Runge-Kutta orde 3 dan orde 2. Oleh karena itu, laman ini hanya akan membahas aplikasi metode Runge-Kutta orde 4. | ||
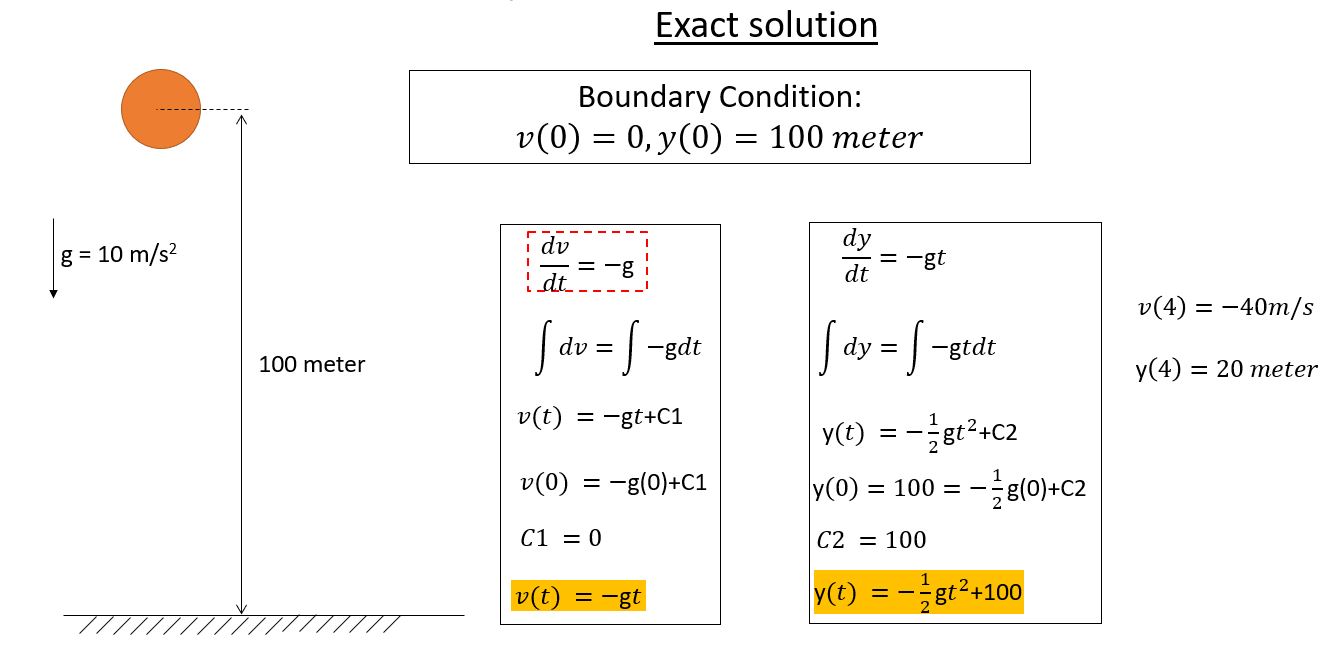
| + | Untuk mendapatkan pemahaman yang lebih baik, mari lihat pemyelesaian persoalan berikut: | ||
| + | |||
| + | [[File:runge-kutta2.JPG]] | ||
| + | |||
| + | [[File:runge-kutta3.JPG]] | ||
| + | |||
| + | [[File:runge-kutta4.JPG]] | ||
| + | |||
| + | [[File:runge-kutta5.JPG]] | ||
| + | |||
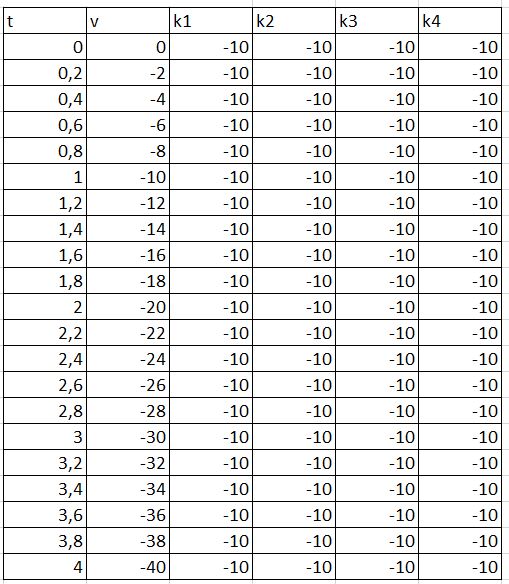
| + | Selanjutnya, pengerjaan dapan dilanjutkandengan menggunakan bantuan spread sheet. Sebelum menggunakan bahasa pemrograman python. Dengan menggunakan Sperad Sheet (Ms.Excel) didapatkan hasil sebagai berikut: | ||
| + | |||
| + | [[File:tabel_runge-kutta1_rev.JPG]] | ||
| + | |||
| + | [[File:tabel_runge-kutta2.JPG]] | ||
| + | |||
| + | |||
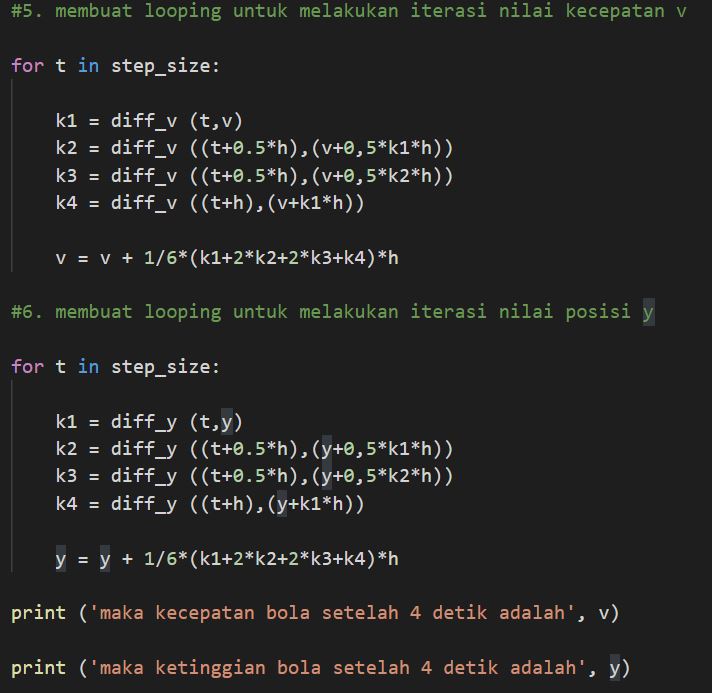
| + | Lalu, selanjutnya metode runge kutta ini dapat diapliakasikan dengan bahasa pemrograman. Berikut algoritma beserta koding metode Runge-kutta untuk soal bola jatuh bebas: | ||
| + | |||
| + | [[File:python_runge-kutta1.JPG]] | ||
| + | [[File:python_runge-kutta2.JPG]] | ||
| + | |||
| + | ==ARTIFICIAL INTELEGENCE: NEURAL-NETWORK== | ||
| + | |||
| + | Seiring dengan berkembangnya zaman, saat ini pengembangan mengenai Artificial Intelegence sangat berkembang dengan pesat. Terlebih lagi sekarang Indonesia sudah mulai memasuki era industri 4.0. Diantara Artificial Intelegence yang sangat banyak diaplikasikan adalah Model Neural Network atau biasa disebut Artificial Neural Network. Prinsip dari Neural Network ini terinsipirasi dari sistem kerja sistem kerja otak manusia. Untuk mengetahui apa itu Neural Network, teman-teman dapat melakukan studi literatur lebih lanjut. | ||
| + | |||
| + | Di page ini, kita akan membahas bagaimana membangun sebuah model Neural Network dengan menggunakan python. Pertama, kita akan membuat model tersebut di python secara kasar atau ''scratch''. Contoh code Neural Network secara scratch dapat dilihat sebagai berikut: | ||
| + | |||
| + | import numpy as np | ||
| + | from numpy import exp as exp | ||
| + | |||
| + | def sigmoid (x): | ||
| + | return 1/(1+exp(-x)) | ||
| + | |||
| + | def sigmoid_derivative (x): | ||
| + | return x*(1-x) | ||
| + | |||
| + | |||
| + | # input sebanyak 4 buah dengan 5 percobaan data | ||
| + | training_input = np.array([[0,0,1,0,1], | ||
| + | [1,1,1,0,1], | ||
| + | [1,0,1,0,1], | ||
| + | [0,1,1,0,1]]) | ||
| + | |||
| + | # nilai output sebanyak 4 buah dengan 2 hasil mendekati nilai eksak | ||
| + | training_output = np.array([[1,1,1,1],[0,0,0,0]]).T | ||
| + | |||
| + | print('training input') | ||
| + | print(training_input) | ||
| + | |||
| + | print('training outputs') | ||
| + | print(training_output) | ||
| + | |||
| + | # pseudo random untuk matrix weight | ||
| + | np.random.seed(1) | ||
| + | |||
| + | # total synaptic weight di matrix neuron 5 kolom 2 baris | ||
| + | # 5 untuk banyak data per input | ||
| + | # 2 untuk banyaknya output | ||
| + | |||
| + | synaptic_weight =2*np.random.random((5,2))+1 | ||
| + | |||
| + | |||
| + | print('random starting synaptic weight') | ||
| + | print(synaptic_weight) | ||
| + | |||
| + | for i in range (2000): | ||
| + | input_layer = training_input | ||
| + | output = sigmoid(np.dot(input_layer, synaptic_weight)) | ||
| + | error = training_output - output | ||
| + | adjustment = error + sigmoid_derivative(output) | ||
| + | synaptic_weight += np.dot(input_layer.T, adjustment) | ||
| + | |||
| + | print('synaptic weight after training') | ||
| + | print(synaptic_weight) | ||
| + | |||
| + | print ('output hasil setelah iterasi') | ||
| + | print(output) | ||
Latest revision as of 11:48, 3 December 2019
Tanggal : 12/02/2019
Contents
PENDAHULUAN
Metode numerik merupakan sebuah metode yang digunakan untuk menyelesaikan berbagai kasus dan masalah matematis melalui komputasi. Metode numerik pada umumnya melibatkan jumlah komputasi yang sangat banyak, dengan melibatkan proses iterasi hitungan. Oleh karena itu, komputasi metode numerik dilakukan dengan menggunakan bantuan komputer. Metode numerik saat ini juga banyak diaplikasikan dalam berbagai bidang, salah satunya dibidang engineering.
Perhitungan metode numerik dapat dilakukan dengan bantuan komputer melalui software atau perangkat lunak yang digunakan khusus untuk perhitungan metode numerik.Software pemrograman juga telah banyak tersedia seecara gratis (Open Source). Salah satu software pemrograman yang cukup umum digunakan saat ini adalah Python. Python merupakan salah satu software yang dapat digunakan untuk melakukan perhitungan metode numerik. Selain bersifat gratis (Open Source), software ini juga banyak diminati karena banyak tersedia library yang memudahkan penggunanya.
Dalam page ini, akan dibahas beberapa bahasan yang telah dibahas di kelas metode numerik departemen teknik mesin FTUI. Diharapkan semua orang yang mengakses page ini dapat mengambil manfaat dan ilmu yang bermanfaat, terutama ilmu mengenai metode numerik. Masukan dan saran sangat diperlukan agar page ini bisa menjadi lebih baik lagi kedepannya.
PYTHON : BASIC
Pada aplikasinya, metodu numerikal dilakukan dengan bantuan software. Diantara software yang saat ini banyak digunakan, terutama didunia industri, khususnya pengembangan revolusi industri 4.0, adalah python Oleh karena itu, sebelum mempelajari metode numerik, ada baiknya terlebih dahulu kita mengenal lebih dekat mengenai software python itu sendiri.
Saat ini, sudah banyak tersebar informasi dan media untuk mempelajari software python, seperti di youtube, website, dan bahkan aplikasi. Salah satu website rujukan yang saya rekomendasikan untuk mempelajari python adalah [1]. Namun, di page ini saya juga akan memberikan beberapa materi dasar mengenai program python.
1. Menampilkan sesuatu menggunakan python "Hellow World"
menampilkan sesuatu pada python, misalnya, sebuah tulisan atau sebuah angka, dapat dilakukan dengan perintah print('tulisan') sebagai contoh berikut:
- under construction
2. Variabel dan Types
-Strings -Number
3. Tupples dan List
4. konveri types
5. operasi aritmatika dasar
6. Condition
7. Loops
8. Input Data
9. Fungsi
-Lambda statement
10. Modules and Dictionary
11. membuat Array
APLIKASI PADA LIMIT FUNGSI
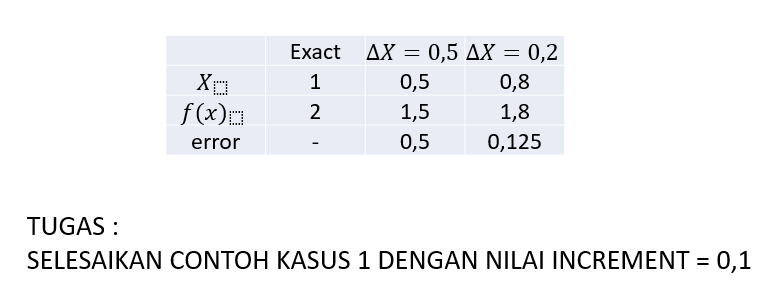
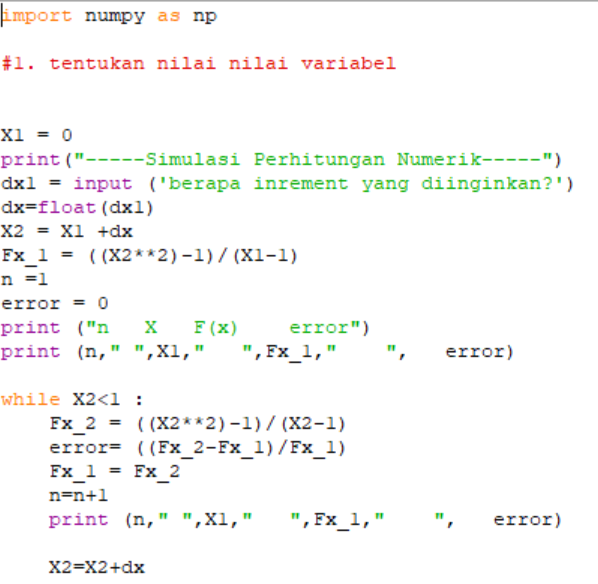
Pembahasan pertama, yaitu contoh sederhana bagaimana cara menyelesaikan persamaan menggunakan metode numerik. Materi singkat mengenai aplikasi metode numerik pada limit sebuah fungsi dapat dilihat sebagai berikut:
Adapun contoh code syntax sederhana perhitungan limit fungsi pada software python adalah
Aplikasi Pada Aljabar Simultan : Eliminasi Gauss
Eliminasi Gauss dapat diaplikasikan untuk menyelesaikan kasus pada aljabar simultan. Eliminasi Gauss juga dapat dilakukan dengan menggunakan metode numerik. Dengan menggunakan metode numerik, perhitungan dapat dilakukan secara efisien dan cepat dengan menggunakan bantuan program python. Berikut dibawah ini merupakan video mengenai konsep dan penjelasan sederhana mengenai Eliminasi Gauss yang dilakukan dengan metode numerik dengan menggunakan program Python.
Aplikasi Aljabar Simultan pada sistem pegas
Sistem Pegas Seri
Sistem pegas seri dapat ditinjau melalu metode finite elemenet analysis (FEA). Dengan FEA, pegas ditinjau pada setiap elemen dengan setiap node yang ada pada masing-masing elemen pegas. Eliminasi Gauss, dengan menggunakan program Python juga dapat digunakan untuk menyelesaikan sistem pegas seri yang ditinjau dengan metode FEA. Tutorial dan penjelasan singkat mengenai penyelesaian sistem pegas seri dengan menggunakan python dapat dilihat pada video berikut:
Metode Numerik untuk persamaan diferrensial-Runge-Kutta
Metode Numerik juga dapat digunakan untuk menyelesaikan persaan diferrensial biasa (Oder Differential Equation) atau yang dikenal dengan ODE. Penggunakan metode numerik untuk menyelesaikan ODE didasarkan pada beberapa hal sebagai berikut: 1.Metode numerik dapat menyelesaikan persaaman differensial biasa secara effektif dan lebih mudah dibandingkan dengan penyelesain secara exact.
2.Terdapat banyak kasus dimana persamaan diferensial biasa tidak bisa diselesaikan secara exact, namun bisa diselesaikan secara numerikal.
3.Pada aplikasinya, sebagian besar persoalan mengenai persamaan differensial biasa diselesaikan menggunakan metode numerik, khususnya di era komputerisasi. Untuk menyelesaikan persamaan differensial biasa secara numerikal, ada beberapa metode yang dapat digunakan, diantaranya adalah metode runge-kutta. Secara mendasar, pendekatan dengan menggunakan metode runge-kutta dapat digambarkan sebgai berikut:
Metode Runge-Kutta terdiri dari beberapa orde, dimuluai dari metode Runge-Kutta orde 2, yaitu metode Rungge-Kutta yang paling sederhana. Metode Rungge-Kutta orde 3 dapat menghasilkan akurasi yang lebih baik. Begitu juga dengan metode Rungge-Kutta orde 4 dapat menghasilkan hasil pendekatan dengan akurasi yang lebih baik dari pada metode Runge-Kutta orde 3 dan orde 2. Oleh karena itu, laman ini hanya akan membahas aplikasi metode Runge-Kutta orde 4. Untuk mendapatkan pemahaman yang lebih baik, mari lihat pemyelesaian persoalan berikut:
Selanjutnya, pengerjaan dapan dilanjutkandengan menggunakan bantuan spread sheet. Sebelum menggunakan bahasa pemrograman python. Dengan menggunakan Sperad Sheet (Ms.Excel) didapatkan hasil sebagai berikut:
Lalu, selanjutnya metode runge kutta ini dapat diapliakasikan dengan bahasa pemrograman. Berikut algoritma beserta koding metode Runge-kutta untuk soal bola jatuh bebas:
ARTIFICIAL INTELEGENCE: NEURAL-NETWORK
Seiring dengan berkembangnya zaman, saat ini pengembangan mengenai Artificial Intelegence sangat berkembang dengan pesat. Terlebih lagi sekarang Indonesia sudah mulai memasuki era industri 4.0. Diantara Artificial Intelegence yang sangat banyak diaplikasikan adalah Model Neural Network atau biasa disebut Artificial Neural Network. Prinsip dari Neural Network ini terinsipirasi dari sistem kerja sistem kerja otak manusia. Untuk mengetahui apa itu Neural Network, teman-teman dapat melakukan studi literatur lebih lanjut.
Di page ini, kita akan membahas bagaimana membangun sebuah model Neural Network dengan menggunakan python. Pertama, kita akan membuat model tersebut di python secara kasar atau scratch. Contoh code Neural Network secara scratch dapat dilihat sebagai berikut:
import numpy as np from numpy import exp as exp
def sigmoid (x):
return 1/(1+exp(-x))
def sigmoid_derivative (x):
return x*(1-x)
- input sebanyak 4 buah dengan 5 percobaan data
training_input = np.array([[0,0,1,0,1],
[1,1,1,0,1],
[1,0,1,0,1],
[0,1,1,0,1]])
- nilai output sebanyak 4 buah dengan 2 hasil mendekati nilai eksak
training_output = np.array([[1,1,1,1],[0,0,0,0]]).T
print('training input') print(training_input)
print('training outputs') print(training_output)
- pseudo random untuk matrix weight
np.random.seed(1)
- total synaptic weight di matrix neuron 5 kolom 2 baris
- 5 untuk banyak data per input
- 2 untuk banyaknya output
synaptic_weight =2*np.random.random((5,2))+1
print('random starting synaptic weight')
print(synaptic_weight)
for i in range (2000):
input_layer = training_input output = sigmoid(np.dot(input_layer, synaptic_weight)) error = training_output - output adjustment = error + sigmoid_derivative(output) synaptic_weight += np.dot(input_layer.T, adjustment)
print('synaptic weight after training') print(synaptic_weight)
print ('output hasil setelah iterasi') print(output)