Difference between revisions of "Kelompok 15"
(→Anggota Kelompok) |
(→CFD - Airdrag) |
||
| (6 intermediate revisions by 2 users not shown) | |||
| Line 4: | Line 4: | ||
1. Jonathan Kevin (1706036513) | 1. Jonathan Kevin (1706036513) | ||
2. Raihan Nurrasyid A (1806149255) | 2. Raihan Nurrasyid A (1806149255) | ||
| − | 3. Wahyu Nugroho Ramadhan | + | 3. Wahyu Nugroho Ramadhan (1806201314) |
== Tugas Kelompok == | == Tugas Kelompok == | ||
| + | === Eliminasi Gauss === | ||
| + | Operasi gaus merupakan salahs atu metode untuk menyelesaikan persamaan matematis. Dari segi bentuk matrik, operasi gaus terdiri dari tiga matriks yaitu matriks koefisien, matriks variabel, dan matriks konstanta. | ||
| − | |||
| − | + | [[File:regaus-1.jpg | 500px | center | thumb | matrik operasi eliminasi gaus yang umum gunakan dalam bentuk matriks terpartisi]] | |
| − | + | ||
| − | + | gambar diatas merupakan contoh dari matrik yang siap dilakukan operasi eliminasi gaus. Bentuk matriksnya disebut matriks terpartisi. Matrik terpartisi sendiri juga terdiri dari matriks koefisien di tiga kolom awal, dan matriks konstanta di kolom terakhir yang dipisahkan dengan garis putus-putus. | |
| − | [- | + | |
| − | [ | + | dari situ, untuk memulai pengkodean ke dalam python, terdapat dua hal yang perlu dipelajari yaitu (1) metriks dan pembuatan matriks di python, dan (2) operasi matriks. |
| − | + | ||
| − | + | untuk memudahkan, kami menggunakan modul numpy yang memiliki model operasi eliminasi gaus dengan syntax linalg. | |
| − | + | ||
| − | + | from numpy import linalg | |
| − | + | import numpy as np | |
| − | + | ||
| − | + | bar1 = [1 , 0 , 0] | |
| + | bar2 = [-1, 1 ,0 ] | ||
| + | bar3 = [ 0, -1 ,1] | ||
| + | |||
| + | f1=3 | ||
| + | f2=2 | ||
| + | f3=3 | ||
| + | |||
| + | nmat = np.array ([bar1,bar2,bar3]) | ||
| + | cons = np.array ([f1 , f2 , f3]) | ||
| + | print(' ') | ||
| + | print ("Matriks Koefisien :") | ||
| + | print(nmat) | ||
| + | print(' ') | ||
| + | print ('Matriks Konstanta :') | ||
| + | print (cons) | ||
| + | print(' ') | ||
| + | |||
| + | jawab = linalg.solve (nmat,cons) | ||
| + | print(jawab) | ||
| + | |||
| + | |||
| + | dalam skrip diatas, terdapat pendefinisian matriks dengan menggunakan syntax "np.array". np dalam syntax itu adalah panggilan untuk numpy dan array adalah subjek yang dipanggil dalam kontkes ini adalah matriks. Kemudian Linalg merupkaan operasi matriks bentuk Ax=B dimana A adalah matriks koeisien, x matriks variabel dan B adalah matriks konstanta. Bentuk Ax=B sendiri adalha bentuk untuk mencari nilai dai matriks variabel. | ||
| + | |||
| + | setelah di run, muncul hasil seperti berikut. | ||
| + | |||
| + | [[File:rehasiloperasi.png | thumb | center | Hasil run skrip diatas]] | ||
| + | |||
| + | |||
| + | === Runge Kutta === | ||
| + | === CFD - Airdrag === | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | [[File:cfdsoff1.jpg|800px|center]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | [[File:cfdsoff2.jpg|800px|center]] | ||
Latest revision as of 16:29, 20 November 2019
Anggota Kelompok
1. Jonathan Kevin (1706036513) 2. Raihan Nurrasyid A (1806149255) 3. Wahyu Nugroho Ramadhan (1806201314)
Tugas Kelompok
Eliminasi Gauss
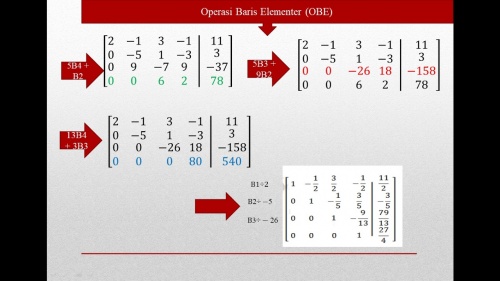
Operasi gaus merupakan salahs atu metode untuk menyelesaikan persamaan matematis. Dari segi bentuk matrik, operasi gaus terdiri dari tiga matriks yaitu matriks koefisien, matriks variabel, dan matriks konstanta.
gambar diatas merupakan contoh dari matrik yang siap dilakukan operasi eliminasi gaus. Bentuk matriksnya disebut matriks terpartisi. Matrik terpartisi sendiri juga terdiri dari matriks koefisien di tiga kolom awal, dan matriks konstanta di kolom terakhir yang dipisahkan dengan garis putus-putus.
dari situ, untuk memulai pengkodean ke dalam python, terdapat dua hal yang perlu dipelajari yaitu (1) metriks dan pembuatan matriks di python, dan (2) operasi matriks.
untuk memudahkan, kami menggunakan modul numpy yang memiliki model operasi eliminasi gaus dengan syntax linalg.
from numpy import linalg import numpy as np
bar1 = [1 , 0 , 0] bar2 = [-1, 1 ,0 ] bar3 = [ 0, -1 ,1] f1=3 f2=2 f3=3
nmat = np.array ([bar1,bar2,bar3])
cons = np.array ([f1 , f2 , f3])
print(' ')
print ("Matriks Koefisien :")
print(nmat)
print(' ')
print ('Matriks Konstanta :')
print (cons)
print(' ')
jawab = linalg.solve (nmat,cons) print(jawab)
dalam skrip diatas, terdapat pendefinisian matriks dengan menggunakan syntax "np.array". np dalam syntax itu adalah panggilan untuk numpy dan array adalah subjek yang dipanggil dalam kontkes ini adalah matriks. Kemudian Linalg merupkaan operasi matriks bentuk Ax=B dimana A adalah matriks koeisien, x matriks variabel dan B adalah matriks konstanta. Bentuk Ax=B sendiri adalha bentuk untuk mencari nilai dai matriks variabel.
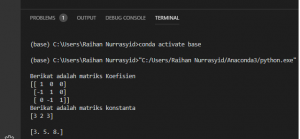
setelah di run, muncul hasil seperti berikut.
Runge Kutta
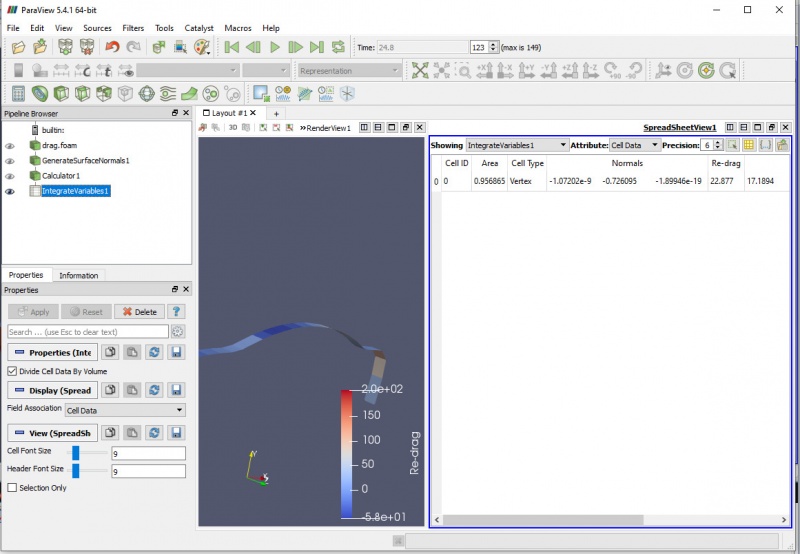
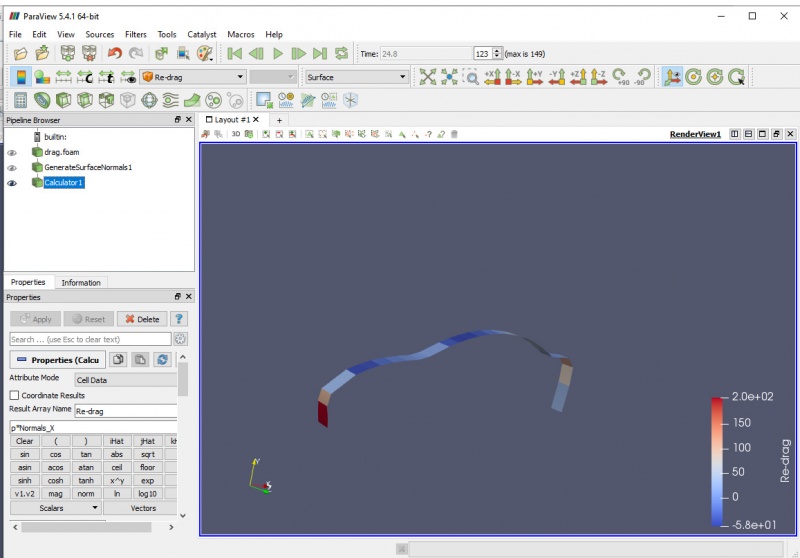
CFD - Airdrag