Difference between revisions of "Gabriella Emristy"
(→Pertemuan 9 (23/10/19)) |
|||
| (17 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
| − | == Pertemuan 1 == | + | == Pertemuan 1 (4/9/19)== |
'''''Mengapa Gaby belajar kalkulus ?''''' Kenapa saya belajar kalkulus? Tidak ada dorongan, hanya takut mama kecewa. | '''''Mengapa Gaby belajar kalkulus ?''''' Kenapa saya belajar kalkulus? Tidak ada dorongan, hanya takut mama kecewa. | ||
| + | |||
'''''Apa itu Python?''''' Python adalah perangkat pemrograman yang cukup sederhana. Dengan perangkat ini kita dapat meminta bantuan komputer untuk menyelesaikan permasalahan yang diberikan dengan metode matematika. Bahasa yang digunakan pun relatif universal, dapat dipahami oleh komputer dan manusia. Terkadang kita mengerti logika penyelesaian masalah, namun kita tidak mampu menghitungnya karena perhitungan yang kompleks. Disinilah peran perangkat phyton. Komputer tidak akan kesulitan untuk menghitung banyak hal dan bilangan, selama kita memasukkan bahasa yang dapat ia mengerti. Kita dapat menemukan jawaban dengan mengaplikasikan langkah-langkah pengerjaannya. Aplikasi skala besarnya adalah, Amerika Serikat bisa memprediksi kapan badai akan datang hanya dengan penggunaan komputer untuk menyelesaikan model matematika dengan model numerik. | '''''Apa itu Python?''''' Python adalah perangkat pemrograman yang cukup sederhana. Dengan perangkat ini kita dapat meminta bantuan komputer untuk menyelesaikan permasalahan yang diberikan dengan metode matematika. Bahasa yang digunakan pun relatif universal, dapat dipahami oleh komputer dan manusia. Terkadang kita mengerti logika penyelesaian masalah, namun kita tidak mampu menghitungnya karena perhitungan yang kompleks. Disinilah peran perangkat phyton. Komputer tidak akan kesulitan untuk menghitung banyak hal dan bilangan, selama kita memasukkan bahasa yang dapat ia mengerti. Kita dapat menemukan jawaban dengan mengaplikasikan langkah-langkah pengerjaannya. Aplikasi skala besarnya adalah, Amerika Serikat bisa memprediksi kapan badai akan datang hanya dengan penggunaan komputer untuk menyelesaikan model matematika dengan model numerik. | ||
| + | |||
'''Rakuman''' | '''Rakuman''' | ||
| Line 15: | Line 17: | ||
Dalam mata kuliah Metode Numerik ini, kami kami akan belajar sedikit-banyak tentang pemrograman. Sebuah hal yang tidak banyak dikuasai anak teknik mesin. Bagi saya, mata kuliah ini cukup menarik. Saya pernah belajar programming dengan bantuan Qbasic. Kini, kami menggunakan Python. Python mudah didapatkan dan mudah digunakan. Aplikasinya bisa luas dan sangat berguna. Di pertemuan pertama ini, kami pun diminta untuk mengisi biodata kami di web ini, air.eng.ac.id. Mata kuliah ini tidak main-main! | Dalam mata kuliah Metode Numerik ini, kami kami akan belajar sedikit-banyak tentang pemrograman. Sebuah hal yang tidak banyak dikuasai anak teknik mesin. Bagi saya, mata kuliah ini cukup menarik. Saya pernah belajar programming dengan bantuan Qbasic. Kini, kami menggunakan Python. Python mudah didapatkan dan mudah digunakan. Aplikasinya bisa luas dan sangat berguna. Di pertemuan pertama ini, kami pun diminta untuk mengisi biodata kami di web ini, air.eng.ac.id. Mata kuliah ini tidak main-main! | ||
| − | == | + | == Tugas 1== |
[[File:gebi1.jpg|400px|thumb|center|]] | [[File:gebi1.jpg|400px|thumb|center|]] | ||
| + | |||
---- | ---- | ||
| − | + | == Pertemuan 2 (11/9/19)== | |
| − | == Pertemuan 2 == | ||
'''''Tahu lebih jauh''''' | '''''Tahu lebih jauh''''' | ||
Saya berhalangan hadir minggu kemarin akibat kurang sehat. Meski begitu, saya belajar lebih jauh soal penggunaan Python itu sendiri. Saya belajar penggunaan rumus if else, dan penggunaan phyton dalam menghitung luas bangun datar.Juga penggunaan while. Saya memahami bahwa Phyton dapat membantu saya dalam menyelesaikan persoalan yang setipe dengan lebih cepat. Terutama bila banyak data yang perlu diolah. Perangkat ini kemudian penggunaannya dapat diaplikasikan ke banyak aspek lainnya. | Saya berhalangan hadir minggu kemarin akibat kurang sehat. Meski begitu, saya belajar lebih jauh soal penggunaan Python itu sendiri. Saya belajar penggunaan rumus if else, dan penggunaan phyton dalam menghitung luas bangun datar.Juga penggunaan while. Saya memahami bahwa Phyton dapat membantu saya dalam menyelesaikan persoalan yang setipe dengan lebih cepat. Terutama bila banyak data yang perlu diolah. Perangkat ini kemudian penggunaannya dapat diaplikasikan ke banyak aspek lainnya. | ||
| + | saya juga membuat tugas atau latihan yang dikelas seperti tercantum | ||
| + | [[File:gebi1.png|400px|thumb|center|]] | ||
| − | |||
| − | == Pertemuan 3 == | + | ---- |
| + | == Pertemuan 3 (18/9/19)== | ||
'''Penggunaan Loop pada Python''' | '''Penggunaan Loop pada Python''' | ||
Kelas hari ini diawali dengan Kuis. Kami diminta untuk membuat command pada Python untuk membantu pengguna program mengetahui nilai suku ke-n dari deret Fibonacci. Kami tidak diizinkan untuk mengaplikasikannya langsung di Python, melainkan di secarik kertas. Proses yang harus kami lewati adalah membuat Algoitma, Flow Chart, barulah cammand program yang dapat di "run". | Kelas hari ini diawali dengan Kuis. Kami diminta untuk membuat command pada Python untuk membantu pengguna program mengetahui nilai suku ke-n dari deret Fibonacci. Kami tidak diizinkan untuk mengaplikasikannya langsung di Python, melainkan di secarik kertas. Proses yang harus kami lewati adalah membuat Algoitma, Flow Chart, barulah cammand program yang dapat di "run". | ||
| + | |||
'''''Algoritma''''' adalah sebuah cara kita mengekspresikan sebuah notasi dengan bahasa yang kita gunakan sehari-hari, bukan bahasa pemrograman.Algoritma seseorang dapat berbeda dengan orang lain. | '''''Algoritma''''' adalah sebuah cara kita mengekspresikan sebuah notasi dengan bahasa yang kita gunakan sehari-hari, bukan bahasa pemrograman.Algoritma seseorang dapat berbeda dengan orang lain. | ||
'''''Flow Chart''''' adalah sebuah cara kita menngerjakan soal yang menggunakan logika dengan sistem diagram yang menghasilkan yes/no untuk hasil yang berbeda. Sistematika flow chart pun tidak melulu sama untuk setiap orang. | '''''Flow Chart''''' adalah sebuah cara kita menngerjakan soal yang menggunakan logika dengan sistem diagram yang menghasilkan yes/no untuk hasil yang berbeda. Sistematika flow chart pun tidak melulu sama untuk setiap orang. | ||
| + | |||
Saya tidak dapat menemukan cara yang sesuai. Saya awalnya mencoba untuk menggunakan "if" pada Python. Mematenkan jawaban "1" di suku ke 1 dan 2, lalu mati langkah untuk suku ke 3 dan seterusnya. | Saya tidak dapat menemukan cara yang sesuai. Saya awalnya mencoba untuk menggunakan "if" pada Python. Mematenkan jawaban "1" di suku ke 1 dan 2, lalu mati langkah untuk suku ke 3 dan seterusnya. | ||
| Line 48: | Line 54: | ||
Gambar di atas menunjukkan hasil pemrograman python untuk deret fibonacci | Gambar di atas menunjukkan hasil pemrograman python untuk deret fibonacci | ||
Pada gambar pertama, n yang dimasukkan bernilai 1. Program tidak dapat menuntaskan masalah bila n lebih dari 2 karena program pada "else" tidak menggunakan "return" | Pada gambar pertama, n yang dimasukkan bernilai 1. Program tidak dapat menuntaskan masalah bila n lebih dari 2 karena program pada "else" tidak menggunakan "return" | ||
| + | |||
Maka dilakukan revisi, sehingga didapat program dan hasil di gambar ke-2, program beroperasi sepenuhnya | Maka dilakukan revisi, sehingga didapat program dan hasil di gambar ke-2, program beroperasi sepenuhnya | ||
| + | |||
'''''Apa kekurangan program?''''' Program tipe ini tidak beroprasi efektif karena program akan memakan waktu lama untuk menghitung nilai n yang besar. Hal ini terjadi karena pada "else" program dibuat untuk menambahkan suku-suku fibonacci terlebih dahulu hingga n yang dimaksud. Program pun membutuhkan waktu untuk proses penambahan tersebut. | '''''Apa kekurangan program?''''' Program tipe ini tidak beroprasi efektif karena program akan memakan waktu lama untuk menghitung nilai n yang besar. Hal ini terjadi karena pada "else" program dibuat untuk menambahkan suku-suku fibonacci terlebih dahulu hingga n yang dimaksud. Program pun membutuhkan waktu untuk proses penambahan tersebut. | ||
| + | |||
| + | |||
| + | Pada pertemuan ke-3 ini kami diberi tugas untuk menyiapkan presentasi sebuah penyajian program untuk menyelesaikan masalah Eliminasi Gauss. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == Pertemuan 4 (25/9/19)== | ||
| + | |||
| + | Pembelajaran kami hari ini dimulai dengan kata "model". Apa itu "model" sebenarnya? | ||
| + | |||
| + | Dalam definisi kata ini ada 3 istilah yang melekat. Sebagai '''''representasi, simplifikasi,''''' dan ''''asumsi'''''. Model sendiri memiliki makna yang unik tergantung penggunaan maupun sudut pandang orang. Bagi saya, Model merupakan simplifikasi dari suatu benda atau hal yang memiliki tujuan untuk merepresentasikan hal yang sulit dibuat ulang. Sudut pandang pak Dai cukup mirip dengan saya akan tetapi saya sendiri masih berasa perlunya pengetahuan saya untuk berkembang sehingga mengerti seluk beluk san makan dari sebuah kata yang diintepretasikan dalam istilah teknik mesin. Kami juga selain mendengarkan sudut pandang pak Dai, kami diberi tugas melakukan eliminasi gauss dimana tugas tersebut sudah dikerjakan di Website kelompok kami. | ||
| + | |||
| + | == Tugas 2== | ||
| + | |||
| + | Tugas di link kelompok 16 | ||
| + | http://air.eng.ui.ac.id/index.php?title=Kelompok_16. | ||
| + | |||
| + | == Pertemuan 5 (2/10/19)== | ||
| + | |||
| + | Pada pertemuan ini kami dikenalkan dengan asisten dari Pak Dai, dan kami diberi penjelasan perihal pengaplikasian matriks ke sistem pegas seri. Setiap pegas memiliki suatu koefisien, seperti pada rumus | ||
| + | |||
| + | F= -k dx | ||
| + | |||
| + | Pegas tersebut apabila disusun secara seri akan memiliki persamaan yang baru sehingga Koefisiennya dapat dijumlahkan sehingga mendapatkan suatu persamaan baru yang mampu diwakili olh rumus lain. Untuk menghitung suatu koefisien dapat dilakukan dengan membuat suatu matriks yang berisi beberapa koefisien pegas (stiffness coeficcient) terusun linier. | ||
| + | |||
| + | [[File:laper3.jpg|thumb|center|]] | ||
| + | |||
| + | == Pertemuan 6 (9/10/19)== | ||
| + | |||
| + | Pada pertemuan kali ini, Pak Dai membri kami penjelasan atas suatu istilah lain yaitu, Kontinu. Kontinu memiliki definis yang sangat luas bagi Pak Dai disini Kontinu berarti segala sesuatu yang meiliki wujud atau nyata, seperti meja, laptop, komputer dan bahkan udara. Udara dianggap kontinu karena Walaupun tidak dapat dilihat udara dapat dirasakan. dan udara dapat dilihat atau dianalisa seperti pada wind tunnel yang dibahas d pelajaran semester lain. Gaya atau Force dalam bahasa inggris merupakan hal yang kontinu dimana gaya tidak dapat dilihat namun dapat dirasakan, tetapi pada zaman sekarang gaya dapat diobservasi melalui peranti lunak yang mampu melakukan Mesh View sehingga dapatdilakukan pengoperasian finite element analysis, dimana dibentuk banya segitiga untukmembuat lekukan suatu benda dan deformasinya untuk memperlihatkan efek suatu benda secara rinci. Pak Dai juga menjelaskan apa arti Diffrensial dan manfaatnya di dunia nyata. Diffrensial dari persamaan jarak : | ||
| + | |||
| + | S= V0t + 0.5at^2 | ||
| + | |||
| + | |||
| + | Untuk menghasilkan suatu persamaan kecepatan. | ||
| + | |||
| + | (Vt)^2= V0^2 + 2as | ||
| + | |||
| + | seberti diatas | ||
| + | |||
| + | == Pertemuan 7 (16/10/19)== | ||
| + | Pada pertemuan kali ini saya tidak dapat hadir kelas, diakrenakan sakit, surat terlampir. Namun saya tetap mengerjakan tugas yang seharusnya menjadi perbaikan quiz take home. Setelah saya berbicara dengan sahabat saya, Fabio Almer, saya jadi mengerti bagaimana cara mngerjakan soal yang diberikan. Ternyata tidak sesulit yang saya kira | ||
| + | Berikut jawaban saya: | ||
| + | |||
| + | from numpy import linalg | ||
| + | import numpy as np | ||
| + | #definisikan matriks A | ||
| + | A1 = [0, 0, 2, 1, 2] | ||
| + | A2 = [0, 1, 0, 2, -1] | ||
| + | A3 = [1, 2, 0, -2, 0] | ||
| + | A4 = [0, 0, 0, -1, 1] | ||
| + | A5 = [0, 1, -1, 1, -1] | ||
| + | nmat = np.array ([A1, A2, A3, A4, A5]) | ||
| + | #definisikan matriks B | ||
| + | B = np.array ([1, 1, -4, -2, -1]) | ||
| + | #Dibawah ini adalah kode untuk memecahkan persamaan aljabar linear bertuliskan (linalg) | ||
| + | jawaban = linalg.solve (nmat,B) | ||
| + | a = int(jawaban[0]) | ||
| + | b = int(jawaban[1]) | ||
| + | c = int(jawaban[2]) | ||
| + | d = int(jawaban[3]) | ||
| + | f = int(jawaban[4]) | ||
| + | #munculkan hasil | ||
| + | print("Jawab : X1 adalah ", a) | ||
| + | print("X2 =", b) | ||
| + | print("X3 =", c) | ||
| + | print("X4 =", d) | ||
| + | print("X5 =", f) | ||
| + | #maka dari cara kedua didapat matriks Xnya adalah | ||
| + | Jawab : X1 adalah 2 | ||
| + | X2 = -2 | ||
| + | X3 = 1 | ||
| + | X4 = 1 | ||
| + | X5 = -1 | ||
| + | |||
| + | Program diatas menggunakan numpy. Dimana numpy sendiri saya masih kurang mengerti, Tetapi setelah dijelaskan fabio saya mulai mengerti setiap makna dari string tersebut. | ||
| + | |||
| + | # Di sini, kita akan menggunakan x0 dan y sebagai titik asal, x sebagai t yang diinginkan, dan h sebagai increment. Kita menggunakan h = 0.01. | ||
| + | x0 = 2 | ||
| + | y = 1 | ||
| + | h = 0.01 | ||
| + | x = float(input("Masukkan nilai t: ")) | ||
| + | if x>0 : | ||
| + | # dydx menyatakan persamaan awal dalam soal. | ||
| + | # Didapat hasil x^2-4y | ||
| + | |||
| + | def dydx(x, y): | ||
| + | return (x**2-4*y) | ||
| + | # Ini merupakan implementasi perhitungan Runge-Kutta. | ||
| + | def rungeKutta(x0, y0, x, h): | ||
| + | n = (int)((x - x0)/h) | ||
| + | y = y0 | ||
| + | for i in range(1, n + 1): | ||
| + | k1 = h * dydx(x0, y) | ||
| + | k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1) | ||
| + | k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2) | ||
| + | k4 = h * dydx(x0 + h, y + k3) | ||
| + | |||
| + | # untuk y selanjutnya | ||
| + | y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | |||
| + | # untuk x selanjutnya | ||
| + | x0 = x0 + h | ||
| + | list.append(y) | ||
| + | return y | ||
| + | print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h)) | ||
| + | kemudian akan didapatkan hasil apabila t=0.03 | ||
| + | input | ||
| + | Masukkan nilai t: 0.03 | ||
| + | Nilai y pada t = 0.03 adalah 1 | ||
| + | |||
| + | Rangekutta adalah metode yang sulit. saya juga masih mempelajari ini berhubung pada pelajaran semester 1 maupun 2 saya tidak mendapat metode rangekutta. | ||
| + | |||
| + | [[File:Gaby3.jpg|thumb|center|]] | ||
| + | |||
| + | == Pertemuan 8 (23/10/19)== | ||
| + | Pada pertemuan ini terdapat UTS yang dapat diralat berikut merupakan jawabannya setelah berkonsultasi dengan sahabat saya Fabio Almer. | ||
| + | |||
| + | Problem A | ||
| + | |||
| + | from math import* | ||
| + | #memasukkan variabel yang dipelukan | ||
| + | g=9.81 | ||
| + | m1=eval(input("massa I dalam kg: ")) | ||
| + | m2=eval(input("massa II dalam kg: ")) | ||
| + | m3=eval(input("massa III dalam kg: ")) | ||
| + | alpha=eval(input("sudut dalam radian: ")) | ||
| + | ms=eval(input("koefisien gesek statis: ")) | ||
| + | y=sin(alpha) | ||
| + | x=cos(alpha) | ||
| + | z=(y-ms*x) | ||
| + | T1=m1*g*z | ||
| + | T2=T1+m2*g*z | ||
| + | T3=T2+m3*g*z | ||
| + | m4=T3/g | ||
| + | print("nilai T1 adalah: ", T1, "Newton") | ||
| + | print("nilai T1 adalah: ", T2, "Newton") | ||
| + | print("nilai T1 adalah: ", T3, "Newton") | ||
| + | print("nilai m4 adalah: ", m4, "kilogram") | ||
| + | |||
| + | |||
| + | Problem B | ||
| + | |||
| + | #memasukkan nilai variabel yang diperlukan | ||
| + | cd=eval(input("koefisien drag: ")) | ||
| + | v0=eval(input("Kecepatan Awal (m/s): ")) | ||
| + | m=eval(input("Massa (kg): ")) | ||
| + | a=eval(input("Percepatan (m/s^2): ")) | ||
| + | vt=eval(input("Kecepatan maksimal (m/s): ")) | ||
| + | #semua dibagi m | ||
| + | fdrag=(cd*vt**(3/2))/m | ||
| + | ft=a | ||
| + | atot=ft-fdrag | ||
| + | t=(vt-v0)/atot | ||
| + | print("waktu mobil listrik untuk mencapai kecepatan tertinggi: ",t, "detik") | ||
| + | |||
| + | Jujur saya sendiri masih sedikit bingung tentang cara membuat program diatas tetapi saya memahami makna dari program tersebut. Pada saat saya mencoba program versi saya yang B gagal dan tidak ada output, dikarenakan kurangnya pengertian atas hal tersebut. UTS saya merasa tenang karena ada take home. Saya mohon tugas saya dapat diterima dengan baik. | ||
| + | |||
| + | |||
| + | A | ||
| + | https://youtu.be/ZnC0J_XeS8U | ||
| + | https://youtu.be/D8F_n0N6ugM | ||
| + | |||
| + | B | ||
| + | Part 1 https://youtu.be/oquSacHYWKI | ||
| + | Part 2 https://youtu.be/FbF73aaRPYU | ||
| + | |||
| + | |||
| + | |||
| + | == Pertemuan 9 (23/10/19)== | ||
| + | |||
| + | Pemodelan Damping Dengan Method Runge Kutta | ||
| + | |||
| + | [[File:gaby10.png|thumb|center|]] | ||
| + | |||
| + | F = m*a (sigma Gaya) | ||
| + | 5t - cv = m*a | ||
| + | a = (5t-cv)/m | ||
| + | dv/dt = (5t-cv)/m | ||
| + | |||
| + | def TurunV(t, v): #Fungsi Turunan V terhadap t | ||
| + | return ((5*t - c*v)/m) | ||
| + | |||
| + | m=eval(input("massa dalam kilogram : ")) | ||
| + | c=eval(input("damper koefisien (Ns/m) : ")) | ||
| + | |||
| + | t0 = 0 #t initial | ||
| + | v0 = 0 #v initial | ||
| + | t = 7 #kecepatan sistem ditanya pada t setelah 7s | ||
| + | h = 0.06 #delta yang digunakan | ||
| + | nilai = (int)((t - t0)/h) #menghitung jumlah increment | ||
| + | for i in range(1, nilai + 1): | ||
| + | |||
| + | k1 = h * TurunV(t0, v0) #runge kutta | ||
| + | k2 = h * TurunV(t0 + 0.5 * h, v0 + 0.5 * k1) | ||
| + | k3 = h * TurunV(t0 + 0.5 * h, v0 + 0.5 * k2) | ||
| + | k4 = h * TurunV(t0 + h, v0 + k3) | ||
| + | |||
| + | v0 = v0 + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) #sigma nilai k1,k2,k3,k4 ke y' yang baru dan membaginya | ||
| + | t0 = t0 + h | ||
| + | print("Velocity dalam Sistem : ",v0, "m/s") | ||
| + | |||
| + | [[File:gaby11.jpg|thumb|center|]] | ||
Latest revision as of 16:31, 13 November 2019
Gaby , puan ini lahir di Bandung tepat pada 7 Maret tahun naga emas. Ia percaya banyak hal besar yang menunggunya di masa depan. Lain hal, kini, ia bangga sekali menjadi bagian dari Teknik Mesin Universitas Indonesia. Puan ini pula merindukan Bandung, terutama toko kopi Djawa di jalan Braga.
Contents
Pertemuan 1 (4/9/19)
Mengapa Gaby belajar kalkulus ? Kenapa saya belajar kalkulus? Tidak ada dorongan, hanya takut mama kecewa.
Apa itu Python? Python adalah perangkat pemrograman yang cukup sederhana. Dengan perangkat ini kita dapat meminta bantuan komputer untuk menyelesaikan permasalahan yang diberikan dengan metode matematika. Bahasa yang digunakan pun relatif universal, dapat dipahami oleh komputer dan manusia. Terkadang kita mengerti logika penyelesaian masalah, namun kita tidak mampu menghitungnya karena perhitungan yang kompleks. Disinilah peran perangkat phyton. Komputer tidak akan kesulitan untuk menghitung banyak hal dan bilangan, selama kita memasukkan bahasa yang dapat ia mengerti. Kita dapat menemukan jawaban dengan mengaplikasikan langkah-langkah pengerjaannya. Aplikasi skala besarnya adalah, Amerika Serikat bisa memprediksi kapan badai akan datang hanya dengan penggunaan komputer untuk menyelesaikan model matematika dengan model numerik.
Rakuman
Dalam mata kuliah Metode Numerik ini, kami kami akan belajar sedikit-banyak tentang pemrograman. Sebuah hal yang tidak banyak dikuasai anak teknik mesin. Bagi saya, mata kuliah ini cukup menarik. Saya pernah belajar programming dengan bantuan Qbasic. Kini, kami menggunakan Python. Python mudah didapatkan dan mudah digunakan. Aplikasinya bisa luas dan sangat berguna. Di pertemuan pertama ini, kami pun diminta untuk mengisi biodata kami di web ini, air.eng.ac.id. Mata kuliah ini tidak main-main!
Tugas 1
Pertemuan 2 (11/9/19)
Tahu lebih jauh
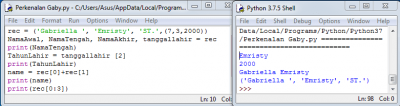
Saya berhalangan hadir minggu kemarin akibat kurang sehat. Meski begitu, saya belajar lebih jauh soal penggunaan Python itu sendiri. Saya belajar penggunaan rumus if else, dan penggunaan phyton dalam menghitung luas bangun datar.Juga penggunaan while. Saya memahami bahwa Phyton dapat membantu saya dalam menyelesaikan persoalan yang setipe dengan lebih cepat. Terutama bila banyak data yang perlu diolah. Perangkat ini kemudian penggunaannya dapat diaplikasikan ke banyak aspek lainnya.
saya juga membuat tugas atau latihan yang dikelas seperti tercantum
Pertemuan 3 (18/9/19)
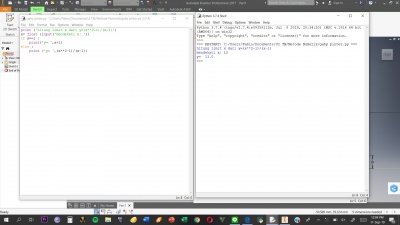
Penggunaan Loop pada Python
Kelas hari ini diawali dengan Kuis. Kami diminta untuk membuat command pada Python untuk membantu pengguna program mengetahui nilai suku ke-n dari deret Fibonacci. Kami tidak diizinkan untuk mengaplikasikannya langsung di Python, melainkan di secarik kertas. Proses yang harus kami lewati adalah membuat Algoitma, Flow Chart, barulah cammand program yang dapat di "run".
Algoritma adalah sebuah cara kita mengekspresikan sebuah notasi dengan bahasa yang kita gunakan sehari-hari, bukan bahasa pemrograman.Algoritma seseorang dapat berbeda dengan orang lain.
Flow Chart adalah sebuah cara kita menngerjakan soal yang menggunakan logika dengan sistem diagram yang menghasilkan yes/no untuk hasil yang berbeda. Sistematika flow chart pun tidak melulu sama untuk setiap orang.
Saya tidak dapat menemukan cara yang sesuai. Saya awalnya mencoba untuk menggunakan "if" pada Python. Mematenkan jawaban "1" di suku ke 1 dan 2, lalu mati langkah untuk suku ke 3 dan seterusnya.
Kuis dikumpulkan, kemudian kami diberi kesempatan untuk mencoba program kami ke komputer. Kami pun diizinkan untuk mencari informasi tambaha dari Internet. Dari situ lah banyak dari kami yang berhasil membuat command. Tetapi saya kini malah stuck dengan program saya yang entah salahnya dimana, tapi tidak bisa dirun.
Kami pun kembali diberi kesempatan untuk mencobanya di rumah, dan hasil kerja kami harus diunggah di akun ini
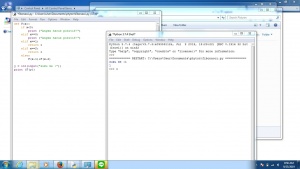
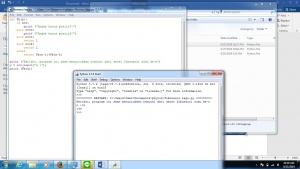
Gambar di atas menunjukkan hasil pemrograman python untuk deret fibonacci Pada gambar pertama, n yang dimasukkan bernilai 1. Program tidak dapat menuntaskan masalah bila n lebih dari 2 karena program pada "else" tidak menggunakan "return"
Maka dilakukan revisi, sehingga didapat program dan hasil di gambar ke-2, program beroperasi sepenuhnya
Apa kekurangan program? Program tipe ini tidak beroprasi efektif karena program akan memakan waktu lama untuk menghitung nilai n yang besar. Hal ini terjadi karena pada "else" program dibuat untuk menambahkan suku-suku fibonacci terlebih dahulu hingga n yang dimaksud. Program pun membutuhkan waktu untuk proses penambahan tersebut.
Pada pertemuan ke-3 ini kami diberi tugas untuk menyiapkan presentasi sebuah penyajian program untuk menyelesaikan masalah Eliminasi Gauss.
Pertemuan 4 (25/9/19)
Pembelajaran kami hari ini dimulai dengan kata "model". Apa itu "model" sebenarnya?
Dalam definisi kata ini ada 3 istilah yang melekat. Sebagai representasi, simplifikasi, dan 'asumsi. Model sendiri memiliki makna yang unik tergantung penggunaan maupun sudut pandang orang. Bagi saya, Model merupakan simplifikasi dari suatu benda atau hal yang memiliki tujuan untuk merepresentasikan hal yang sulit dibuat ulang. Sudut pandang pak Dai cukup mirip dengan saya akan tetapi saya sendiri masih berasa perlunya pengetahuan saya untuk berkembang sehingga mengerti seluk beluk san makan dari sebuah kata yang diintepretasikan dalam istilah teknik mesin. Kami juga selain mendengarkan sudut pandang pak Dai, kami diberi tugas melakukan eliminasi gauss dimana tugas tersebut sudah dikerjakan di Website kelompok kami.
Tugas 2
Tugas di link kelompok 16 http://air.eng.ui.ac.id/index.php?title=Kelompok_16.
Pertemuan 5 (2/10/19)
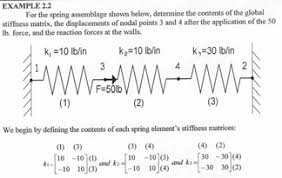
Pada pertemuan ini kami dikenalkan dengan asisten dari Pak Dai, dan kami diberi penjelasan perihal pengaplikasian matriks ke sistem pegas seri. Setiap pegas memiliki suatu koefisien, seperti pada rumus
F= -k dx
Pegas tersebut apabila disusun secara seri akan memiliki persamaan yang baru sehingga Koefisiennya dapat dijumlahkan sehingga mendapatkan suatu persamaan baru yang mampu diwakili olh rumus lain. Untuk menghitung suatu koefisien dapat dilakukan dengan membuat suatu matriks yang berisi beberapa koefisien pegas (stiffness coeficcient) terusun linier.
Pertemuan 6 (9/10/19)
Pada pertemuan kali ini, Pak Dai membri kami penjelasan atas suatu istilah lain yaitu, Kontinu. Kontinu memiliki definis yang sangat luas bagi Pak Dai disini Kontinu berarti segala sesuatu yang meiliki wujud atau nyata, seperti meja, laptop, komputer dan bahkan udara. Udara dianggap kontinu karena Walaupun tidak dapat dilihat udara dapat dirasakan. dan udara dapat dilihat atau dianalisa seperti pada wind tunnel yang dibahas d pelajaran semester lain. Gaya atau Force dalam bahasa inggris merupakan hal yang kontinu dimana gaya tidak dapat dilihat namun dapat dirasakan, tetapi pada zaman sekarang gaya dapat diobservasi melalui peranti lunak yang mampu melakukan Mesh View sehingga dapatdilakukan pengoperasian finite element analysis, dimana dibentuk banya segitiga untukmembuat lekukan suatu benda dan deformasinya untuk memperlihatkan efek suatu benda secara rinci. Pak Dai juga menjelaskan apa arti Diffrensial dan manfaatnya di dunia nyata. Diffrensial dari persamaan jarak :
S= V0t + 0.5at^2
Untuk menghasilkan suatu persamaan kecepatan.
(Vt)^2= V0^2 + 2as
seberti diatas
Pertemuan 7 (16/10/19)
Pada pertemuan kali ini saya tidak dapat hadir kelas, diakrenakan sakit, surat terlampir. Namun saya tetap mengerjakan tugas yang seharusnya menjadi perbaikan quiz take home. Setelah saya berbicara dengan sahabat saya, Fabio Almer, saya jadi mengerti bagaimana cara mngerjakan soal yang diberikan. Ternyata tidak sesulit yang saya kira
Berikut jawaban saya:
from numpy import linalg
import numpy as np
#definisikan matriks A
A1 = [0, 0, 2, 1, 2]
A2 = [0, 1, 0, 2, -1]
A3 = [1, 2, 0, -2, 0]
A4 = [0, 0, 0, -1, 1]
A5 = [0, 1, -1, 1, -1]
nmat = np.array ([A1, A2, A3, A4, A5])
#definisikan matriks B
B = np.array ([1, 1, -4, -2, -1])
#Dibawah ini adalah kode untuk memecahkan persamaan aljabar linear bertuliskan (linalg)
jawaban = linalg.solve (nmat,B)
a = int(jawaban[0])
b = int(jawaban[1])
c = int(jawaban[2])
d = int(jawaban[3])
f = int(jawaban[4])
#munculkan hasil
print("Jawab : X1 adalah ", a)
print("X2 =", b)
print("X3 =", c)
print("X4 =", d)
print("X5 =", f)
#maka dari cara kedua didapat matriks Xnya adalah
Jawab : X1 adalah 2
X2 = -2
X3 = 1
X4 = 1
X5 = -1
Program diatas menggunakan numpy. Dimana numpy sendiri saya masih kurang mengerti, Tetapi setelah dijelaskan fabio saya mulai mengerti setiap makna dari string tersebut.
# Di sini, kita akan menggunakan x0 dan y sebagai titik asal, x sebagai t yang diinginkan, dan h sebagai increment. Kita menggunakan h = 0.01.
x0 = 2
y = 1
h = 0.01
x = float(input("Masukkan nilai t: "))
if x>0 :
# dydx menyatakan persamaan awal dalam soal.
# Didapat hasil x^2-4y
def dydx(x, y):
return (x**2-4*y)
# Ini merupakan implementasi perhitungan Runge-Kutta.
def rungeKutta(x0, y0, x, h):
n = (int)((x - x0)/h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
k4 = h * dydx(x0 + h, y + k3)
# untuk y selanjutnya
y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# untuk x selanjutnya
x0 = x0 + h
list.append(y)
return y
print("Nilai y pada t =", x, "adalah", rungeKutta(x0, y, x, h))
kemudian akan didapatkan hasil apabila t=0.03
input Masukkan nilai t: 0.03 Nilai y pada t = 0.03 adalah 1
Rangekutta adalah metode yang sulit. saya juga masih mempelajari ini berhubung pada pelajaran semester 1 maupun 2 saya tidak mendapat metode rangekutta.
Pertemuan 8 (23/10/19)
Pada pertemuan ini terdapat UTS yang dapat diralat berikut merupakan jawabannya setelah berkonsultasi dengan sahabat saya Fabio Almer.
Problem A
from math import*
#memasukkan variabel yang dipelukan
g=9.81
m1=eval(input("massa I dalam kg: "))
m2=eval(input("massa II dalam kg: "))
m3=eval(input("massa III dalam kg: "))
alpha=eval(input("sudut dalam radian: "))
ms=eval(input("koefisien gesek statis: "))
y=sin(alpha)
x=cos(alpha)
z=(y-ms*x)
T1=m1*g*z
T2=T1+m2*g*z
T3=T2+m3*g*z
m4=T3/g
print("nilai T1 adalah: ", T1, "Newton")
print("nilai T1 adalah: ", T2, "Newton")
print("nilai T1 adalah: ", T3, "Newton")
print("nilai m4 adalah: ", m4, "kilogram")
Problem B
#memasukkan nilai variabel yang diperlukan
cd=eval(input("koefisien drag: "))
v0=eval(input("Kecepatan Awal (m/s): "))
m=eval(input("Massa (kg): "))
a=eval(input("Percepatan (m/s^2): "))
vt=eval(input("Kecepatan maksimal (m/s): "))
#semua dibagi m
fdrag=(cd*vt**(3/2))/m
ft=a
atot=ft-fdrag
t=(vt-v0)/atot
print("waktu mobil listrik untuk mencapai kecepatan tertinggi: ",t, "detik")
Jujur saya sendiri masih sedikit bingung tentang cara membuat program diatas tetapi saya memahami makna dari program tersebut. Pada saat saya mencoba program versi saya yang B gagal dan tidak ada output, dikarenakan kurangnya pengertian atas hal tersebut. UTS saya merasa tenang karena ada take home. Saya mohon tugas saya dapat diterima dengan baik.
A
https://youtu.be/ZnC0J_XeS8U
https://youtu.be/D8F_n0N6ugM
B Part 1 https://youtu.be/oquSacHYWKI Part 2 https://youtu.be/FbF73aaRPYU
Pertemuan 9 (23/10/19)
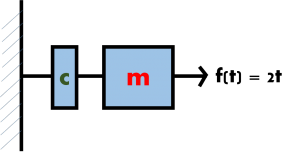
Pemodelan Damping Dengan Method Runge Kutta
F = m*a (sigma Gaya) 5t - cv = m*a a = (5t-cv)/m dv/dt = (5t-cv)/m
def TurunV(t, v): #Fungsi Turunan V terhadap t return ((5*t - c*v)/m)
m=eval(input("massa dalam kilogram : "))
c=eval(input("damper koefisien (Ns/m) : "))
t0 = 0 #t initial
v0 = 0 #v initial
t = 7 #kecepatan sistem ditanya pada t setelah 7s
h = 0.06 #delta yang digunakan
nilai = (int)((t - t0)/h) #menghitung jumlah increment
for i in range(1, nilai + 1):
k1 = h * TurunV(t0, v0) #runge kutta
k2 = h * TurunV(t0 + 0.5 * h, v0 + 0.5 * k1)
k3 = h * TurunV(t0 + 0.5 * h, v0 + 0.5 * k2)
k4 = h * TurunV(t0 + h, v0 + k3)
v0 = v0 + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) #sigma nilai k1,k2,k3,k4 ke y' yang baru dan membaginya
t0 = t0 + h
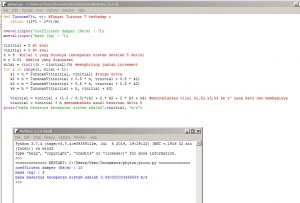
print("Velocity dalam Sistem : ",v0, "m/s")