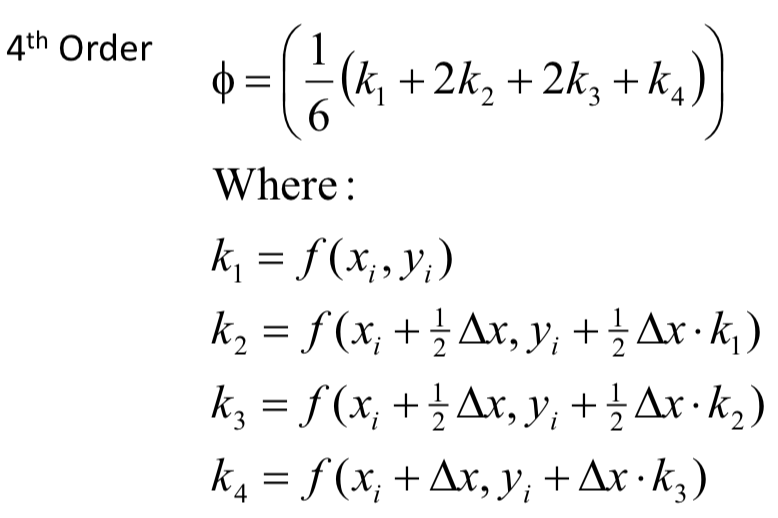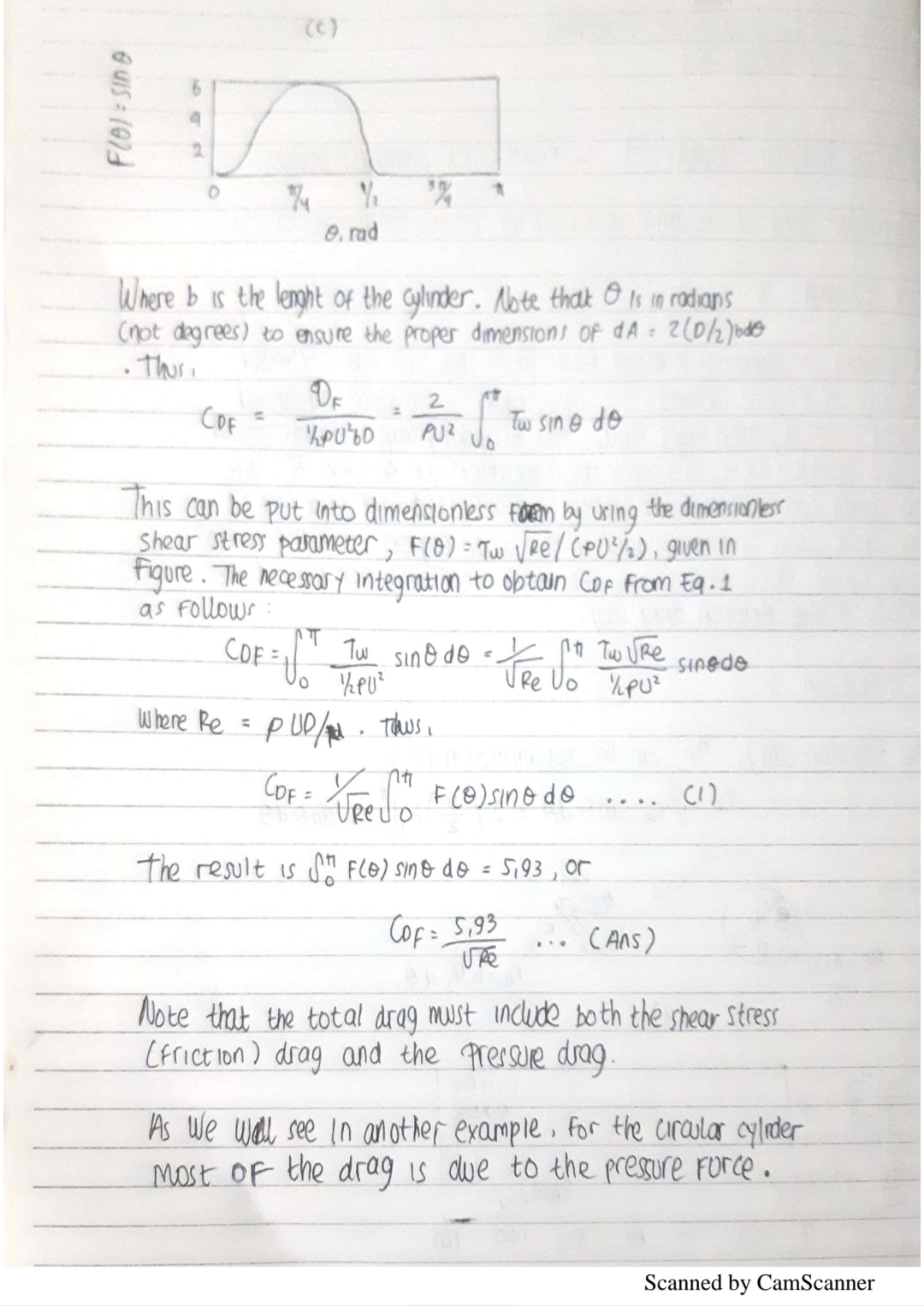Difference between revisions of "Muhammad Salim Al Haddar"
(→Video Muhasabah diri) |
|||
| (14 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
Perkenalkan : | Perkenalkan : | ||
| − | [[]] | + | [[File:IMG_6717.jpg]] |
Nama : Muhammad Salim Al Haddar | Nama : Muhammad Salim Al Haddar | ||
| Line 56: | Line 56: | ||
[[File:Screenshot_2019-10-13_at_17.49.34.png]] | [[File:Screenshot_2019-10-13_at_17.49.34.png]] | ||
| + | |||
[[File:Screenshot_2019-10-13_at_17.51.30.png]] | [[File:Screenshot_2019-10-13_at_17.51.30.png]] | ||
| + | |||
[[File:Screenshot_2019-10-13_at_19.04.23.png]] | [[File:Screenshot_2019-10-13_at_19.04.23.png]] | ||
| + | |||
[[File:Screenshot_2019-10-13_at_17.56.59.png]] | [[File:Screenshot_2019-10-13_at_17.56.59.png]] | ||
| + | |||
| + | == Quis 1 Persiapan UTS == | ||
| + | |||
| + | 1. Problem set 2.1 No.6 halaman 55 pengerjaan di python | ||
| + | |||
| + | Pada soal ini matrix yang diberikan soal adalah sebagai berikut, | ||
| + | |||
| + | A = [[0, 0, 2, 1, 2], [0, 1, 0, 2, -1], [1, 2, 0, -2, 0], [0, 0, 0, -1, 1], [0, 1, -1, 1, -1]] | ||
| + | |||
| + | B = [1, 1, -4, -2, -1] | ||
| + | |||
| + | sebelum memasuki eleminasi gauss, matrix tersebut harus dikonfigurasi ulang agar bisa dihitung, | ||
| + | |||
| + | konfigurasi matrix, | ||
| + | |||
| + | A = [[1, 2, 0, -2, 0], [0, 1, 0, 2, -1],[0, 1, -1, 1, -1], [0, 0, 0, -1, 1], [0, 0, 2, 1, 2]] | ||
| + | |||
| + | B = [-4, 1, -1, -2, 1] | ||
| + | |||
| + | maka hasil yang akan didapatkan adalah, | ||
| + | |||
| + | X1 = 2 | ||
| + | |||
| + | X2 = -2 | ||
| + | |||
| + | X3 = 1 | ||
| + | |||
| + | X4 = 1 | ||
| + | |||
| + | X5 = -1 | ||
| + | |||
| + | kode python | ||
| + | import numpy as np | ||
| + | |||
| + | A=np.array([[1, 2, 0, -2, 0], [0, 1, 0, 2, -1],[0, 1, -1, 1, -1], [0, 0, 0, -1, 1], [0, 0, 2, 1, 2]],float) | ||
| + | |||
| + | B=np.array([-4, 1, -1, -2, 1],float) | ||
| + | |||
| + | n=len(A) | ||
| + | |||
| + | for k in range (0,n-1): for i in range (k+1, n): if A[i,k]!=0 : lam= A[i,k]/A[k,k] A[i,k:n]= A[i, k:n]-(A[k,k:n]*lam) B[i]=B[i]-(B[k]*lam) print ('matrix A:', '\n', A) x=np.zeros(n,float) for m in range (n-1, -1, -1): x[m]=(B[m]-np.dot(A[m, m+1:n], x[m+1:n]))/A[m,m] print ('nilai X', m+1, '=', x[m]) | ||
| + | |||
| + | [[File:Pytonsalim22.png]] | ||
| + | |||
| + | |||
| + | [[File:Python23.png]] | ||
| + | |||
| + | [[File:salimpython.jpg]] | ||
| + | |||
| + | 2. problem set 7.1 no.1 hal 263 | ||
| + | |||
| + | [[File:Pythonism22.jpg]] | ||
| + | |||
| + | [[File:Pythonism2.jpg]] | ||
| + | |||
| + | |||
| + | |||
| + | hasil tersebut memiliki error dari rumus analitis sebesar +2.0880e-12 | ||
| + | |||
| + | == UTS == | ||
| + | |||
| + | Soal 1 | ||
| + | |||
| + | import numpy as np | ||
| + | |||
| + | print('berapa nilai m1?') | ||
| + | a =eval(input()) | ||
| + | |||
| + | print('berapa nilai m2?') | ||
| + | b =eval(input()) | ||
| + | |||
| + | print('berapa nilai m3?') | ||
| + | c =eval(input()) | ||
| + | |||
| + | print('berapa nilai m4?') | ||
| + | d =eval(input()) | ||
| + | |||
| + | alfa=d/(a+b+c) | ||
| + | |||
| + | print('berarti sinus alfa adalah',alfa) | ||
| + | |||
| + | sudutalfa=math.asin(alfa) | ||
| + | |||
| + | sudutalfa2=math.degrees(sudutalfa) | ||
| + | |||
| + | print('jadi nilai sudut alfa adalah',sudutalfa2) | ||
| + | |||
| + | |||
| + | 1. Pertanyaan untuk fungsi | ||
| + | |||
| + | print('Diberikan fungsi sin teta = m4/(m1+m2+m3)') print('Nilai m1?') m1=eval(input()) print('Nilai m2?') m2=eval(input()) print('Nilai m3?') m3=eval(input()) print('Nilai m4?') m4=eval(input()) | ||
| + | |||
| + | 2. Menentukan nilai a | ||
| + | a = 0 | ||
| + | |||
| + | 3. Menentukan fungsi sin teta | ||
| + | x = m4 y = (m1+m2+m3) result = x / y | ||
| + | |||
| + | 4. Mendapatkan hasil sin teta | ||
| + | print('Jadi, hasil sin teta adalah', result) | ||
| + | |||
| + | |||
| + | Soal 2 | ||
| + | |||
| + | import numpy as np | ||
| + | |||
| + | a = 10 b = 1 c = 2 def diff_v (t,v): | ||
| + | |||
| + | fungsi = a - b -c | ||
| + | |||
| + | return (fungsi) | ||
| + | |||
| + | v = 0 | ||
| + | |||
| + | h = 1 step_size = np.arange (0,10,h) | ||
| + | |||
| + | for t in step_size: | ||
| + | |||
| + | k1 = diff_v (t,v) | ||
| + | |||
| + | k2 = diff_v ((t+0.5*h), (v+0.5*k1*h)) | ||
| + | |||
| + | k3 = diff_v ((t+0.5*h), (v+0.5*k2*h)) | ||
| + | |||
| + | k4 = diff_v ((t+h), (v+k1*h)) | ||
| + | |||
| + | v = v + 1/6*(k1+2*k2+2*k3+k4)*h | ||
| + | |||
| + | print ('maka v setelah 10 detik adalah', v) | ||
| + | |||
| + | == Video Muhasabah diri == | ||
| + | |||
| + | <youtube>https://youtu.be/AoRU1bxYWCU</youtube> | ||
| + | |||
| + | == Video UTS == | ||
| + | |||
| + | <youtube>https://youtu.be/VKUaVK2ET9g</youtube> | ||
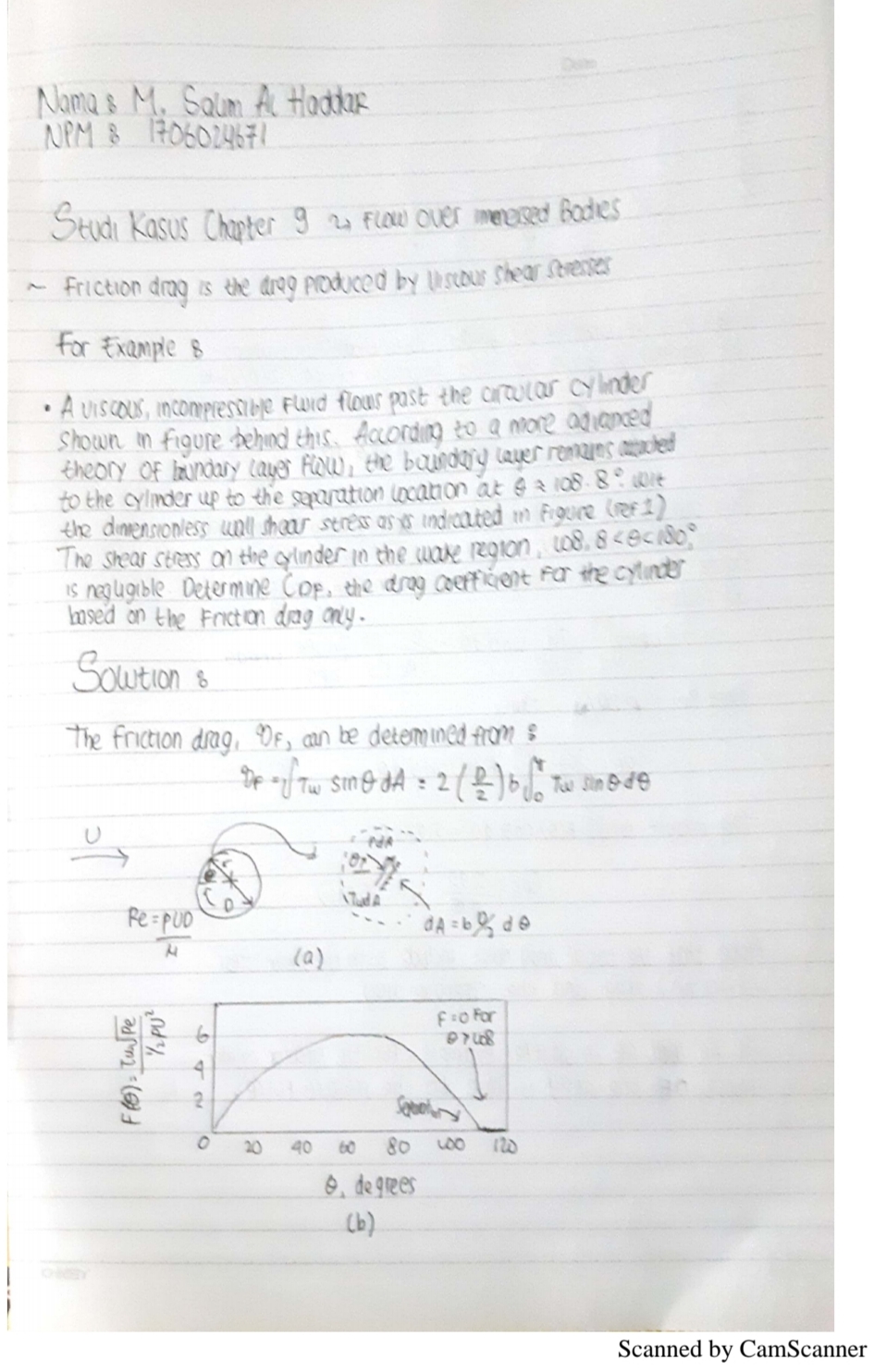
=='''MEKANIKA FLUIDA'''== | =='''MEKANIKA FLUIDA'''== | ||
Latest revision as of 22:42, 28 October 2019
Perkenalkan :
Nama : Muhammad Salim Al Haddar
Npm : 1706024671
Contents
METODE NUMERIK
Hiburan 1
Pada pertemuan perdana, awal dari semester 5, kelas metode numerik pun dimulai. Tentu biasanya pada pertemuan pertama Pak dosen menyuruh untuk memperkenalkan diri, tapi sebelum itu kedua dosen pada mata kuliah ini dua-duanya masuk pada pertemuan pertama dan kita satu kelas ikut berdikusi, setelah berdikusi tentang pokok-pokok kehidupan, kami para mahasiswa langsung disuruh memperkenalkan dirinya masing-masing pada web ini; Muhammad Salim Al Haddar atau Salim ( lahir di Jakarta, 27 Oktober 1999; umur 19 tahun ) adalah seorang mahasiswa Universitas Indonesia dengan jurusan Teknik Mesin. Diterima di Universitas Indonesia pada tahun 2017 dan sudah menjalani masa perkuliahan selama 2 tahun. Sebelumnya, Salim adalah siswa dari SMA Negeri 68 Jakarta yang berlokasi pada Jalan Salemba, Jakarta Pusat. Sedang tempat tinggalnya di kawasan Jakarta Timur, masih tidak terlalu jauh dari kampus UI Depok, sehingga ia pun dan keluarga memutuskan mengekos tidak diperlukan. Ia pun menjalani 2 tahun kuliah ini dengan pulang pergi atau yang lebih dikenal dengan singkatan PP. Ini adalah lanjutan dari studi di Teknik Mesin dengan judul mata kuliah ‘Metode Numerik’. Selamat menjalani hidup dan jangan lupa bersyukur.
Hiburan 2
Belajar aplikasi Phyton
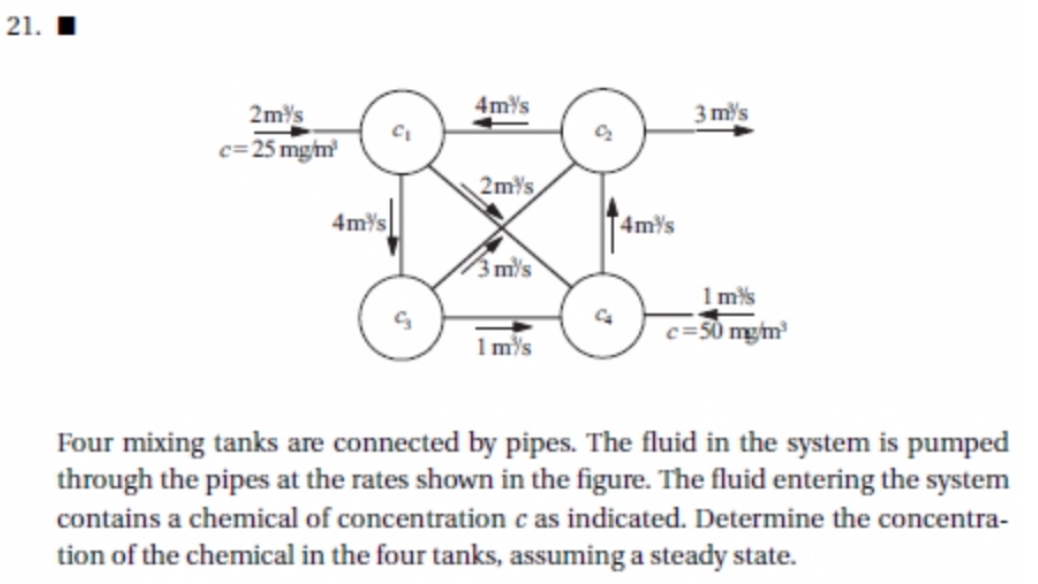
Hiburan 3
Langkah penyelesaian Mencari persamaan pada gambar tersebut 6c1 - 4c2 = 50
-2c1 - c3 + 4c4 = 50
7c2 - 3c3 - 4c4 = 50
-4c1 + 4c3 = 50
dan didapatkan matriks
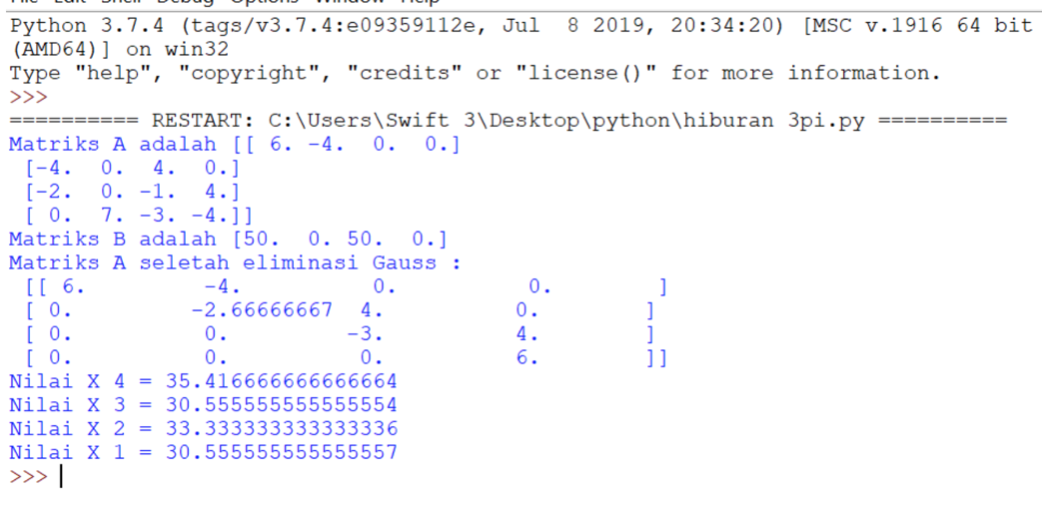
[6. -4. 0. 0.]
[-4. 0. 4. 0.]
[-2. 0. -1. 4.]
[0. 7. -3. -4.]
Kemudian dikerjakan menggunakan python

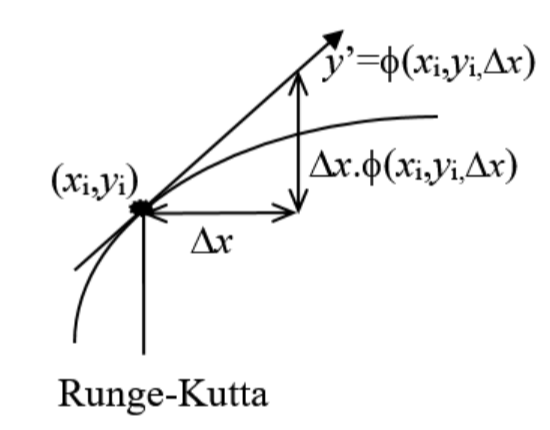
Hiburan 4
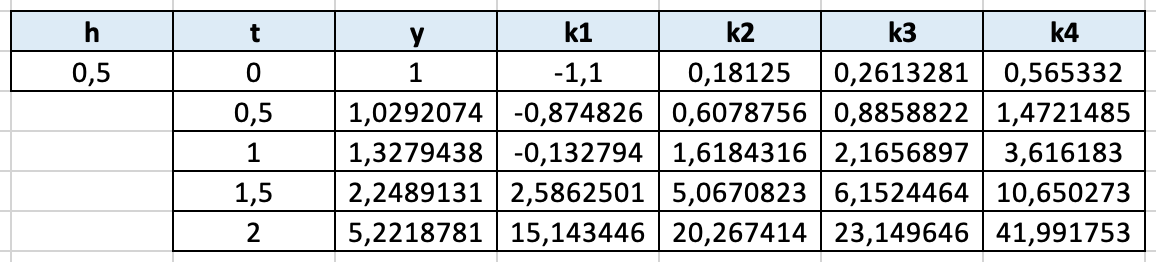
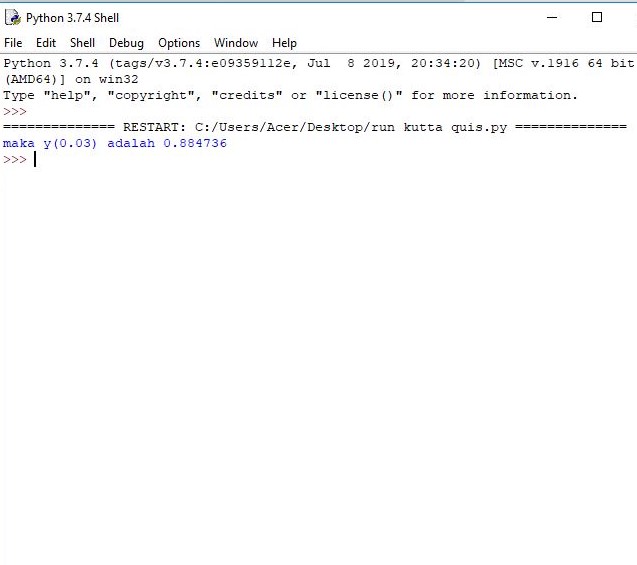
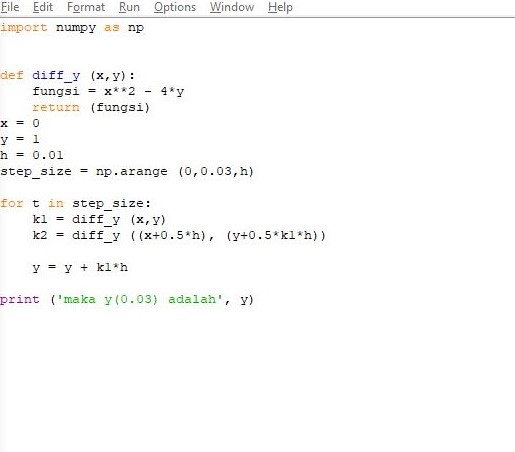
The classical fourth-order runge-kutta method
Quis 1 Persiapan UTS
1. Problem set 2.1 No.6 halaman 55 pengerjaan di python
Pada soal ini matrix yang diberikan soal adalah sebagai berikut,
A = [[0, 0, 2, 1, 2], [0, 1, 0, 2, -1], [1, 2, 0, -2, 0], [0, 0, 0, -1, 1], [0, 1, -1, 1, -1]]
B = [1, 1, -4, -2, -1]
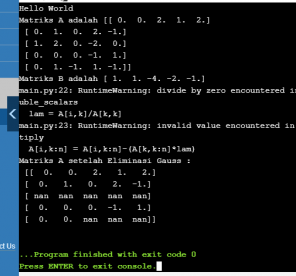
sebelum memasuki eleminasi gauss, matrix tersebut harus dikonfigurasi ulang agar bisa dihitung,
konfigurasi matrix,
A = [[1, 2, 0, -2, 0], [0, 1, 0, 2, -1],[0, 1, -1, 1, -1], [0, 0, 0, -1, 1], [0, 0, 2, 1, 2]]
B = [-4, 1, -1, -2, 1]
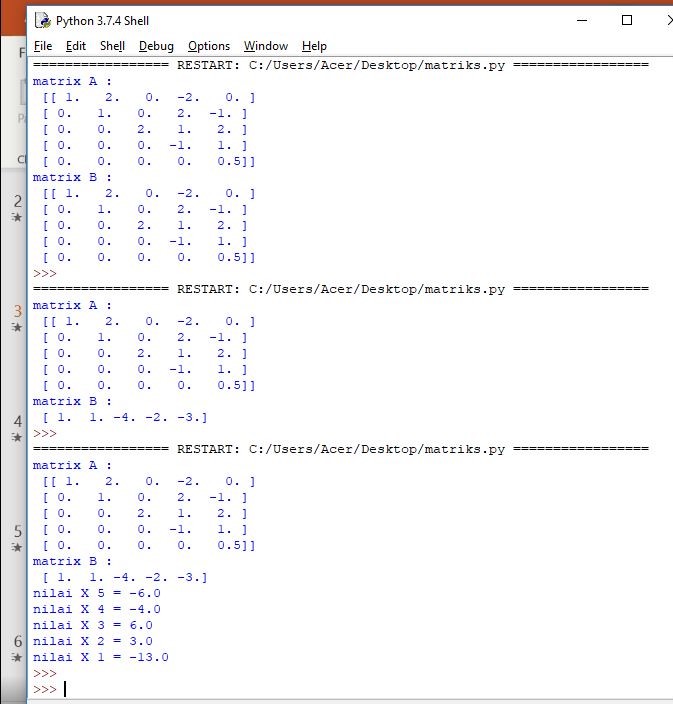
maka hasil yang akan didapatkan adalah,
X1 = 2
X2 = -2
X3 = 1
X4 = 1
X5 = -1
kode python import numpy as np
A=np.array([[1, 2, 0, -2, 0], [0, 1, 0, 2, -1],[0, 1, -1, 1, -1], [0, 0, 0, -1, 1], [0, 0, 2, 1, 2]],float)
B=np.array([-4, 1, -1, -2, 1],float)
n=len(A)
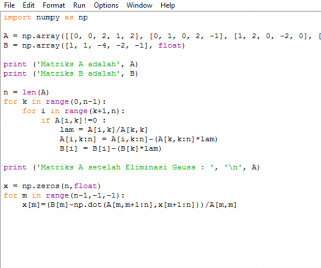
for k in range (0,n-1): for i in range (k+1, n): if A[i,k]!=0 : lam= A[i,k]/A[k,k] A[i,k:n]= A[i, k:n]-(A[k,k:n]*lam) B[i]=B[i]-(B[k]*lam) print ('matrix A:', '\n', A) x=np.zeros(n,float) for m in range (n-1, -1, -1): x[m]=(B[m]-np.dot(A[m, m+1:n], x[m+1:n]))/A[m,m] print ('nilai X', m+1, '=', x[m])
2. problem set 7.1 no.1 hal 263
hasil tersebut memiliki error dari rumus analitis sebesar +2.0880e-12
UTS
Soal 1
import numpy as np
print('berapa nilai m1?') a =eval(input())
print('berapa nilai m2?') b =eval(input())
print('berapa nilai m3?') c =eval(input())
print('berapa nilai m4?') d =eval(input())
alfa=d/(a+b+c)
print('berarti sinus alfa adalah',alfa)
sudutalfa=math.asin(alfa)
sudutalfa2=math.degrees(sudutalfa)
print('jadi nilai sudut alfa adalah',sudutalfa2)
1. Pertanyaan untuk fungsi
print('Diberikan fungsi sin teta = m4/(m1+m2+m3)') print('Nilai m1?') m1=eval(input()) print('Nilai m2?') m2=eval(input()) print('Nilai m3?') m3=eval(input()) print('Nilai m4?') m4=eval(input())
2. Menentukan nilai a a = 0
3. Menentukan fungsi sin teta x = m4 y = (m1+m2+m3) result = x / y
4. Mendapatkan hasil sin teta print('Jadi, hasil sin teta adalah', result)
Soal 2
import numpy as np
a = 10 b = 1 c = 2 def diff_v (t,v): fungsi = a - b -c
return (fungsi)
v = 0
h = 1 step_size = np.arange (0,10,h)
for t in step_size:
k1 = diff_v (t,v) k2 = diff_v ((t+0.5*h), (v+0.5*k1*h))
k3 = diff_v ((t+0.5*h), (v+0.5*k2*h))
k4 = diff_v ((t+h), (v+k1*h)) v = v + 1/6*(k1+2*k2+2*k3+k4)*h
print ('maka v setelah 10 detik adalah', v)