Difference between revisions of "Nadhif Rizki Priambodo"
| (12 intermediate revisions by the same user not shown) | |||
| Line 8: | Line 8: | ||
| − | + | HASIL QUIZ | |
| − | |||
coding | coding | ||
| + | |||
| + | No.1 | ||
| + | |||
print ("QUIZ nadhif rizki p - 1706026140") | print ("QUIZ nadhif rizki p - 1706026140") | ||
A = np.array([[1, 2, 0, -2, 0], [0, 1, 0, 2, -1], [0, 1, -1, 1, -1], [0, 0, 0, -1, 1], [0, 0, 2, 1, 2]], float) | A = np.array([[1, 2, 0, -2, 0], [0, 1, 0, 2, -1], [0, 1, -1, 1, -1], [0, 0, 0, -1, 1], [0, 0, 2, 1, 2]], float) | ||
| Line 35: | Line 37: | ||
SCREENSHOT HASIL | SCREENSHOT HASIL | ||
| + | [[File:Bob.PNG]] | ||
| + | |||
| + | NO.2 | ||
| + | |||
| + | import numpy as np from run_kut4 import * from printSoln import * from math import exp | ||
| + | |||
| + | x = 0.03 def F(x,y): | ||
| + | |||
| + | F = np.zeros(1) | ||
| + | F[0] = ((31/32)*exp(-4))+((1/4)*x**2)-(1/8)*x+(1/32) | ||
| + | return F | ||
| + | x = 0.0 xStop = 0.03 y = np.array([160]) h = 0.01 freq = 1 | ||
| + | |||
| + | print(y) | ||
| + | |||
| + | X,Y = integrate(F,x,y,xStop,h) printSoln(X,Y,freq) input("\nPress return to exit") | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | == UTS Nadhif rizki p == | ||
| + | |||
| + | [nomor 1] | ||
| + | LINK VIDEO : https://www.youtube.com/watch?v=jyrRxuiw6QE | ||
| + | |||
| + | import numpy as np | ||
| + | class GEPP(): | ||
| + | def __init__(self, A, b, doPricing=True): | ||
| + | #super(GEPP, self).__init__() | ||
| + | |||
| + | self.A = A # input: A is an n x n numpy matrix | ||
| + | self.b = b # b is an n x 1 numpy array | ||
| + | self.doPricing = doPricing | ||
| + | |||
| + | self.n = None # n is the length of A | ||
| + | self.x = None # x is the solution of Ax=b | ||
| + | |||
| + | self._validate_input() # method that validates input | ||
| + | self._elimination() # method that conducts elimination | ||
| + | self._backsub() # method that conducts back-substitution | ||
| + | |||
| + | def _validate_input(self): | ||
| + | self.n = len(self.A) | ||
| + | if self.b.size != self.n: | ||
| + | raise ValueError("Invalid argument: incompatible sizes between" + | ||
| + | "A & b.", self.b.size, self.n) | ||
| + | |||
| + | def _elimination(self): | ||
| + | """ | ||
| + | k represents the current pivot row. Since GE traverses the matrix in the | ||
| + | upper right triangle, we also use k for indicating the k-th diagonal | ||
| + | column index. | ||
| + | :return | ||
| + | """ | ||
| + | |||
| + | # Elimination | ||
| + | for k in range(self.n - 1): | ||
| + | if self.doPricing: | ||
| + | # Pivot | ||
| + | maxindex = abs(self.A[k:, k]).argmax() + k | ||
| + | if self.A[maxindex, k] == 0: | ||
| + | raise ValueError("Matrix is singular.") | ||
| + | # Swap | ||
| + | if maxindex != k: | ||
| + | self.Ak, maxindex = self.Amaxindex, k | ||
| + | self.bk, maxindex = self.bmaxindex, k | ||
| + | else: | ||
| + | if self.A[k, k] == 0: | ||
| + | raise ValueError("Pivot element is zero. Try setting doPricing to True.") | ||
| + | # Eliminate | ||
| + | for row in range(k + 1, self.n): | ||
| + | multiplier = self.A[row, k] / self.A[k, k] | ||
| + | self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:] | ||
| + | self.b[row] = self.b[row] - multiplier * self.b[k] | ||
| + | |||
| + | def _backsub(self): | ||
| + | # Back Substitution | ||
| + | |||
| + | self.x = np.zeros(self.n) | ||
| + | for k in range(self.n - 1, -1, -1): | ||
| + | self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k] | ||
| + | |||
| + | |||
| + | def main(): | ||
| + | A = np.array([[1., 0., 0., 0.], | ||
| + | [-1., 1., 0., 0.], | ||
| + | [0., 0., -1., 1.], | ||
| + | [0., 0., 0., 1.]]) | ||
| + | b = np.array([[50.], | ||
| + | [20.], | ||
| + | [5.], | ||
| + | [10.]]) | ||
| + | |||
| + | GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False) | ||
| + | print(GaussElimPiv.x) | ||
| + | print(GaussElimPiv.A) | ||
| + | print(GaussElimPiv.b) | ||
| + | GaussElimPiv = GEPP(A, b) | ||
| + | print(GaussElimPiv.x) | ||
| + | |||
| + | if __name__ == "__main__": | ||
| + | main() | ||
| + | |||
| + | SOAL NOMOR 2 | ||
| + | |||
| + | LINK VIDEO : https://www.youtube.com/watch?v=84Wtcoaow2Q | ||
| + | |||
| + | [[File:Noice.PNG]] | ||
| + | |||
| + | |||
| + | MUHASABAH DIRI NADHIF UNTUK JADI LEBIH BAIK | ||
| + | |||
| + | https://www.youtube.com/watch?v=U0VI7IZAV9s&feature=youtu.be | ||
| + | |||
| + | == Headline text == | ||
Latest revision as of 04:17, 28 October 2019
[Nama : Nadhif rizki priambodo]
[Semester : 5]
[Npm : 1706026140]
Mengikuti lomba kompetisi mobil hemat energi dan shell eco marathon tahun 2018-2020
HASIL QUIZ
coding
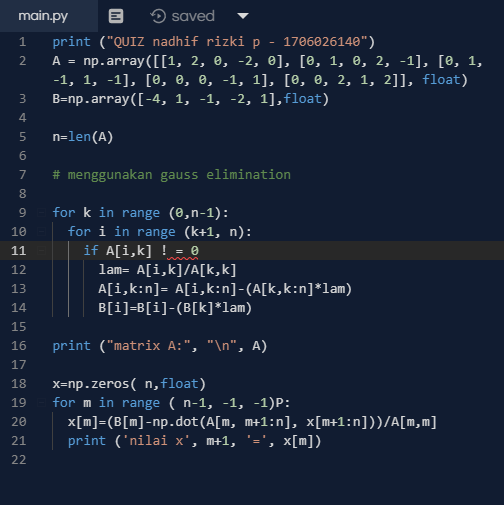
No.1
print ("QUIZ nadhif rizki p - 1706026140") A = np.array([[1, 2, 0, -2, 0], [0, 1, 0, 2, -1], [0, 1, -1, 1, -1], [0, 0, 0, -1, 1], [0, 0, 2, 1, 2]], float) B=np.array([-4, 1, -1, -2, 1],float)
n=len(A)
- menggunakan gauss elimination
for k in range (0,n-1):
for i in range (k+1, n):
if A[i,k] ! = 0
lam= A[i,k]/A[k,k]
A[i,k:n]= A[i,k:n]-(A[k,k:n]*lam)
B[i]=B[i]-(B[k]*lam)
print ("matrix A:", "\n", A)
x=np.zeros( n,float) for m in range ( n-1, -1, -1)P:
x[m]=(B[m]-np.dot(A[m, m+1:n], x[m+1:n]))/A[m,m]
print ('nilai x', m+1, '=', x[m])
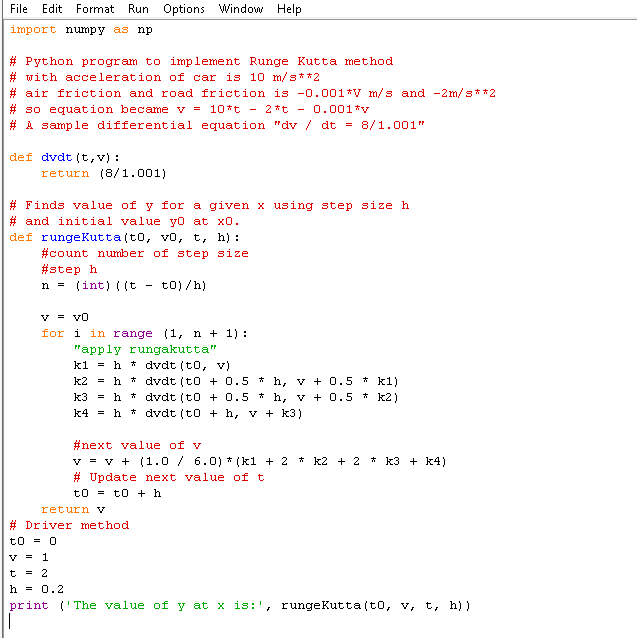
NO.2
import numpy as np from run_kut4 import * from printSoln import * from math import exp
x = 0.03 def F(x,y):
F = np.zeros(1) F[0] = ((31/32)*exp(-4))+((1/4)*x**2)-(1/8)*x+(1/32) return F
x = 0.0 xStop = 0.03 y = np.array([160]) h = 0.01 freq = 1
print(y)
X,Y = integrate(F,x,y,xStop,h) printSoln(X,Y,freq) input("\nPress return to exit")
UTS Nadhif rizki p
[nomor 1] LINK VIDEO : https://www.youtube.com/watch?v=jyrRxuiw6QE
import numpy as np class GEPP():
def __init__(self, A, b, doPricing=True):
#super(GEPP, self).__init__()
self.A = A # input: A is an n x n numpy matrix
self.b = b # b is an n x 1 numpy array
self.doPricing = doPricing
self.n = None # n is the length of A
self.x = None # x is the solution of Ax=b
self._validate_input() # method that validates input
self._elimination() # method that conducts elimination
self._backsub() # method that conducts back-substitution
def _validate_input(self):
self.n = len(self.A)
if self.b.size != self.n:
raise ValueError("Invalid argument: incompatible sizes between" +
"A & b.", self.b.size, self.n)
def _elimination(self):
"""
k represents the current pivot row. Since GE traverses the matrix in the
upper right triangle, we also use k for indicating the k-th diagonal
column index.
:return
"""
# Elimination
for k in range(self.n - 1):
if self.doPricing:
# Pivot
maxindex = abs(self.A[k:, k]).argmax() + k
if self.A[maxindex, k] == 0:
raise ValueError("Matrix is singular.")
# Swap
if maxindex != k:
self.Ak, maxindex = self.Amaxindex, k
self.bk, maxindex = self.bmaxindex, k
else:
if self.A[k, k] == 0:
raise ValueError("Pivot element is zero. Try setting doPricing to True.")
# Eliminate
for row in range(k + 1, self.n):
multiplier = self.A[row, k] / self.A[k, k]
self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:]
self.b[row] = self.b[row] - multiplier * self.b[k]
def _backsub(self):
# Back Substitution
self.x = np.zeros(self.n)
for k in range(self.n - 1, -1, -1):
self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k]
def main():
A = np.array([[1., 0., 0., 0.],
[-1., 1., 0., 0.],
[0., 0., -1., 1.],
[0., 0., 0., 1.]])
b = np.array([[50.],
[20.],
[5.],
[10.]])
GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False) print(GaussElimPiv.x) print(GaussElimPiv.A) print(GaussElimPiv.b) GaussElimPiv = GEPP(A, b) print(GaussElimPiv.x)
if __name__ == "__main__":
main()
SOAL NOMOR 2
LINK VIDEO : https://www.youtube.com/watch?v=84Wtcoaow2Q
MUHASABAH DIRI NADHIF UNTUK JADI LEBIH BAIK
https://www.youtube.com/watch?v=U0VI7IZAV9s&feature=youtu.be