Difference between revisions of "Illiyyin Lafi Abrarri"
IlliyyinLafi (talk | contribs) |
(→UTS) |
||
| (37 intermediate revisions by 2 users not shown) | |||
| Line 6: | Line 6: | ||
== Biografi == | == Biografi == | ||
| − | Illiyyin Lafi Abrarri lahir di Surabaya, 23 Mei 1999 dari pasangan suami istri Amir Hamzah dan Dwi Riawati. Mengawali pendidikan mulai dari sekolah dasar hingga SMA di Surabaya. berasal dari SMAN 15 Surabaya dan melanjutkan pendidikan S1 di Teknik Mesin Universitas Indonesia. memiliki hobi bermain game, renang, dan badminton. | + | [[File:1482205277676.jpg|300px]] |
| + | |||
| + | Illiyyin Lafi Abrarri dengan NPM 1706070772 lahir di Surabaya, 23 Mei 1999 dari pasangan suami istri Amir Hamzah dan Dwi Riawati. Mengawali pendidikan mulai dari sekolah dasar hingga SMA di Surabaya. berasal dari SMAN 15 Surabaya dan melanjutkan pendidikan S1 di Teknik Mesin Universitas Indonesia. memiliki hobi bermain game, renang, dan badminton. | ||
== Karier == | == Karier == | ||
| Line 40: | Line 42: | ||
dan membuat sebuah persamaan yang bias dihitung persamaan linear sederhana | dan membuat sebuah persamaan yang bias dihitung persamaan linear sederhana | ||
| − | == | + | ==Hiburan metode numerik 1 A== |
| − | + | Dalam mengerjakan soal (x^2-1)/(x-1) dengan x=1 tidak bisa mendapatkan hasil yang benar dikarenakan 0/0. Oleh sebab itu, saya gunakan limit pendekatan x=1. Soal dikerjakan dengan menambahkan perbedaan 1/9999999 yang mendekati angka nol sehingga hampir tidak merubah hasil dengan menggunakan module coding sebagai berikut | |
| + | |||
[[File:1568464116160.jpg]] | [[File:1568464116160.jpg]] | ||
| + | |||
| + | Pada module ini, saya memisahkan antara pembilang dan penyebut nya sehingga memudahkan perhitungan. | ||
| + | |||
| + | dan memiliki hasil seperti berikut | ||
| + | |||
| + | [[File:1568602744591.jpg]] | ||
| + | |||
| + | ==Hiburan metode numerik 1 B== | ||
| + | [[File:1568603204429.jpg]] | ||
| + | |||
| + | pada soal ini digunakan metode Newton Raphson sebagai metode mencari faktor dari persamaan tersebut | ||
| + | |||
| + | [[File:Modified+Newton-Raphson+Method.jpg]] | ||
| + | |||
| + | dengan module sebagai berikut | ||
| + | |||
| + | [[File:1568464103427.jpg]] | ||
| + | |||
| + | dan mendapatkan hasil sebagai berikut | ||
| + | |||
| + | [[File:1568603830247.jpg]] | ||
| + | |||
| + | dengan flowchart sebagai berikut | ||
| + | |||
| + | [[File:1568605080666.jpg]] | ||
| + | |||
| + | == Hiburan 02- LAFI == | ||
| + | pada tugas hiburan ini | ||
| + | |||
| + | [[File:S__18382858.jpg]] | ||
| + | |||
| + | dikerjakan menggunakan hukum kontinuitas massa dimana masa yang masuk akan sama dengan yang dikeluarkan sehingga didapati rumus Q*''p''=Q*''p'' sehingga akan mendapatakan 4 persamaan dengan 4 variabel | ||
| + | |||
| + | |||
| + | 6C1 - 4C2 = 50 | ||
| + | |||
| + | -2C1 - 1C3 + 4C4 = 50 | ||
| + | |||
| + | 7C2 - 3C3 - 4C4 = 0 | ||
| + | |||
| + | -4C1 + 4C3 = 0 | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | 6C1 - 4C2 + 0C3 + 0C4 = 50 | ||
| + | |||
| + | -2C1 + 0C2 - 1C3 + 4C4 = 50 | ||
| + | |||
| + | 0C1 + 7C2 - 3C3 - 4C4 = 0 | ||
| + | |||
| + | -4C1 + 0C2 + 4C3 + 0C4 = 0 | ||
| + | |||
| + | yang kemudian dijadikan dalam modue python lalu didapatkan nilai C1 = 275/9 , C2 = 100/3 , C3 = 275/9, C4 = 425/12 | ||
| + | |||
| + | |||
| + | |||
| + | import numpy as np | ||
| + | |||
| + | class GEPP(): | ||
| + | |||
| + | def __init__(self, A, b, doPricing=True): | ||
| + | #super(GEPP, self).__init__() | ||
| + | |||
| + | self.A = A # input: A is an n x n numpy matrix | ||
| + | self.b = b # b is an n x 1 numpy array | ||
| + | self.doPricing = doPricing | ||
| + | |||
| + | self.n = None # n is the length of A | ||
| + | self.x = None # x is the solution of Ax=b | ||
| + | |||
| + | self._validate_input() # method that validates input | ||
| + | self._elimination() # method that conducts elimination | ||
| + | self._backsub() # method that conducts back-substitution | ||
| + | def _validate_input(self): | ||
| + | self.n = len(self.A) | ||
| + | if self.b.size != self.n: | ||
| + | raise ValueError("Invalid argument: incompatible sizes between" + | ||
| + | "A & b.", self.b.size, self.n) | ||
| + | |||
| + | def _elimination(self): | ||
| + | """ | ||
| + | k represents the current pivot row. Since GE traverses the matrix in the | ||
| + | upper right triangle, we also use k for indicating the k-th diagonal | ||
| + | column index. | ||
| + | :return | ||
| + | """ | ||
| + | |||
| + | # Elimination | ||
| + | for k in range(self.n - 1): | ||
| + | if self.doPricing: | ||
| + | # Pivot | ||
| + | maxindex = abs(self.A[k:, k]).argmax() + k | ||
| + | if self.A[maxindex, k] == 0: | ||
| + | raise ValueError("Matrix is singular.") | ||
| + | # Swap | ||
| + | if maxindex != k: | ||
| + | self.A[[k, maxindex]] = self.A[[maxindex, k]] | ||
| + | self.b[[k, maxindex]] = self.b[[maxindex, k]] | ||
| + | else: | ||
| + | if self.A[k, k] == 0: | ||
| + | raise ValueError("Pivot element is zero. Try setting doPricing to True.") | ||
| + | # Eliminate | ||
| + | for row in range(k + 1, self.n): | ||
| + | multiplier = self.A[row, k] / self.A[k, k] | ||
| + | self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:] | ||
| + | self.b[row] = self.b[row] - multiplier * self.b[k] | ||
| + | |||
| + | def _backsub(self): | ||
| + | # Back Substitution | ||
| + | self.x = np.zeros(self.n) | ||
| + | for k in range(self.n - 1, -1, -1): | ||
| + | self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k] | ||
| + | def main(): | ||
| + | A = np.array([[6., -4., 0., 0.], | ||
| + | [-4., 0., 4., 0.], | ||
| + | [-2., 0., -1., 4.], | ||
| + | [0., 7., -3., -4.]]) | ||
| + | b = np.array([[50.], | ||
| + | [0.], | ||
| + | [50.], | ||
| + | [0.]]) | ||
| + | print("ini matriks awal nya") | ||
| + | print(A) | ||
| + | print("ini hasil yang awal") | ||
| + | print(b) | ||
| + | |||
| + | GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False) | ||
| + | print("ini hasil akhirnya") | ||
| + | print(GaussElimPiv.x) | ||
| + | print(GaussElimPiv.A) | ||
| + | print(GaussElimPiv.b) | ||
| + | GaussElimPiv = GEPP(A, b) | ||
| + | print(GaussElimPiv.x) | ||
| + | if __name__ == "__main__": | ||
| + | main() | ||
| + | |||
| + | ==quiz == | ||
| + | 1. | ||
| + | import numpy as np | ||
| + | |||
| + | |||
| + | class GEPP(): | ||
| + | |||
| + | def __init__(self, A, b, doPricing=True): | ||
| + | |||
| + | |||
| + | self.A = A | ||
| + | self.b = b | ||
| + | self.doPricing = doPricing | ||
| + | |||
| + | self.n = None | ||
| + | self.x = None | ||
| + | |||
| + | self._validate_input() | ||
| + | self._elimination() | ||
| + | self._backsub() | ||
| + | |||
| + | def _validate_input(self): | ||
| + | self.n = len(self.A) | ||
| + | if self.b.size != self.n: | ||
| + | raise ValueError("yah bingung.", self.b.size, self.n) | ||
| + | |||
| + | def _elimination(self): | ||
| + | |||
| + | |||
| + | # Elimination | ||
| + | for k in range(self.n - 1): | ||
| + | if self.doPricing: | ||
| + | # Pivot | ||
| + | maxindex = abs(self.A[k:, k]).argmax() + k | ||
| + | if self.A[maxindex, k] == 0: | ||
| + | raise ValueError("Matrix ini singular.") | ||
| + | # Swap | ||
| + | if maxindex != k: | ||
| + | self.A[[k, maxindex]] = self.A[[maxindex, k]] | ||
| + | self.b[[k, maxindex]] = self.b[[maxindex, k]] | ||
| + | else: | ||
| + | if self.A[k, k] == 0: | ||
| + | raise ValueError("coba lagi.") | ||
| + | # Eliminate | ||
| + | for row in range(k + 1, self.n): | ||
| + | multiplier = self.A[row, k] / self.A[k, k] | ||
| + | self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:] | ||
| + | self.b[row] = self.b[row] - multiplier * self.b[k] | ||
| + | |||
| + | def _backsub(self): | ||
| + | # Back Substitution | ||
| + | |||
| + | self.x = np.zeros(self.n) | ||
| + | for k in range(self.n - 1, -1, -1): | ||
| + | self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k] | ||
| + | |||
| + | |||
| + | def main(): | ||
| + | A = np.array([[1., 2., 0., -2., 0.], | ||
| + | [0., 1., 0., 2., -1.], | ||
| + | [0., 1., -1., 1., -1.], | ||
| + | [0., 0., 2., 1., 2.], | ||
| + | [0., 0., 0., -1., 1.]]) | ||
| + | b = np.array([[-4.], | ||
| + | [1.], | ||
| + | [-1.], | ||
| + | [1.], | ||
| + | [-2.]]) | ||
| + | GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False) | ||
| + | print(GaussElimPiv.x) | ||
| + | print(GaussElimPiv.A) | ||
| + | print(GaussElimPiv.b) | ||
| + | GaussElimPiv = GEPP(A, b) | ||
| + | print(GaussElimPiv.x) | ||
| + | |||
| + | if __name__ == "__main__": | ||
| + | main() | ||
| + | #pada persamaan ke 3 dan ke 1 ditukar karena variabel awal tidak boleh bernilai nol | ||
| + | |||
| + | 2. | ||
| + | |||
| + | import numpy as np | ||
| + | from run_kut4 import * | ||
| + | from printSoln import * | ||
| + | from math import exp | ||
| + | |||
| + | x = 0.03 | ||
| + | def F(x,y): | ||
| + | F = np.zeros(1) | ||
| + | F[0] = ((31/32)*exp(-4))+((1/4)*x**2)-(1/8)*x+(1/32) | ||
| + | return F | ||
| + | |||
| + | x = 0.0 | ||
| + | xStop = 0.03 | ||
| + | y = np.array([160]) | ||
| + | h = 0.01 | ||
| + | freq = 1 | ||
| + | |||
| + | print(y) | ||
| + | |||
| + | X,Y = integrate(F,x,y,xStop,h) | ||
| + | printSoln(X,Y,freq) | ||
| + | input("\nPress return to exit") | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==UTS== | ||
| + | A. | ||
| + | |||
| + | https://www.youtube.com/watch?v=Lar9ahvi2ew | ||
| + | |||
| + | |||
| + | import numpy as np | ||
| + | class GEPP(): | ||
| + | def __init__(self, A, b, doPricing=True): | ||
| + | #super(GEPP, self).__init__() | ||
| + | |||
| + | self.A = A # input: A is an n x n numpy matrix | ||
| + | self.b = b # b is an n x 1 numpy array | ||
| + | self.doPricing = doPricing | ||
| + | |||
| + | self.n = None # n is the length of A | ||
| + | self.x = None # x is the solution of Ax=b | ||
| + | |||
| + | self._validate_input() # method that validates input | ||
| + | self._elimination() # method that conducts elimination | ||
| + | self._backsub() # method that conducts back-substitution | ||
| + | |||
| + | def _validate_input(self): | ||
| + | self.n = len(self.A) | ||
| + | if self.b.size != self.n: | ||
| + | raise ValueError("Invalid argument: incompatible sizes between" + | ||
| + | "A & b.", self.b.size, self.n) | ||
| + | |||
| + | def _elimination(self): | ||
| + | """ | ||
| + | k represents the current pivot row. Since GE traverses the matrix in the | ||
| + | upper right triangle, we also use k for indicating the k-th diagonal | ||
| + | column index. | ||
| + | :return | ||
| + | """ | ||
| + | |||
| + | # Elimination | ||
| + | for k in range(self.n - 1): | ||
| + | if self.doPricing: | ||
| + | # Pivot | ||
| + | maxindex = abs(self.A[k:, k]).argmax() + k | ||
| + | if self.A[maxindex, k] == 0: | ||
| + | raise ValueError("Matrix is singular.") | ||
| + | # Swap | ||
| + | if maxindex != k: | ||
| + | self.A[[k, maxindex]] = self.A[[maxindex, k]] | ||
| + | self.b[[k, maxindex]] = self.b[[maxindex, k]] | ||
| + | else: | ||
| + | if self.A[k, k] == 0: | ||
| + | raise ValueError("Pivot element is zero. Try setting doPricing to True.") | ||
| + | # Eliminate | ||
| + | for row in range(k + 1, self.n): | ||
| + | multiplier = self.A[row, k] / self.A[k, k] | ||
| + | self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:] | ||
| + | self.b[row] = self.b[row] - multiplier * self.b[k] | ||
| + | |||
| + | def _backsub(self): | ||
| + | # Back Substitution | ||
| + | |||
| + | self.x = np.zeros(self.n) | ||
| + | for k in range(self.n - 1, -1, -1): | ||
| + | self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k] | ||
| + | |||
| + | |||
| + | def main(): | ||
| + | A = np.array([[1., 0., 0., 0.], | ||
| + | [-1., 1., 0., 0.], | ||
| + | [0., 0., -1., 1.], | ||
| + | [0., 0., 0., 1.]]) | ||
| + | b = np.array([[50.], | ||
| + | [20.], | ||
| + | [5.], | ||
| + | [10.]]) | ||
| + | |||
| + | GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False) | ||
| + | print(GaussElimPiv.x) | ||
| + | print(GaussElimPiv.A) | ||
| + | print(GaussElimPiv.b) | ||
| + | GaussElimPiv = GEPP(A, b) | ||
| + | print(GaussElimPiv.x) | ||
| + | |||
| + | if __name__ == "__main__": | ||
| + | main() | ||
| + | |||
| + | |||
| + | B. | ||
| + | |||
| + | dengan asumsi percepatan mobil sebesar 10m/s**2 | ||
| + | |||
| + | perlambatan gesek jalan sebesar 2m/s**2 | ||
| + | |||
| + | dan perlambatan karena gesek udara yang dipengaruhi oleh kecepatan 0,001*v | ||
| + | |||
| + | https://www.youtube.com/watch?v=ystTyu-qooA | ||
| + | |||
| + | import numpy as np | ||
| + | |||
| + | # Python program to implement Runge Kutta method | ||
| + | # with acceleration of car is 10 m/s**2 | ||
| + | # air friction and road friction is -0.001*V m/s and -2m/s**2 | ||
| + | # so equation became v = 10*t - 2*t - 0.001*v | ||
| + | # A sample differential equation "dv / dt = 8/1.001" | ||
| + | |||
| + | def dvdt(t,v): | ||
| + | return (8/1.001) | ||
| + | |||
| + | # Finds value of y for a given x using step size h | ||
| + | # and initial value y0 at x0. | ||
| + | def rungeKutta(t0, v0, t, h): | ||
| + | #count number of step size | ||
| + | #step h | ||
| + | n = (int)((t - t0)/h) | ||
| + | |||
| + | v = v0 | ||
| + | for i in range (1, n + 1): | ||
| + | "apply rungakutta" | ||
| + | k1 = h * dvdt(t0, v) | ||
| + | k2 = h * dvdt(t0 + 0.5 * h, v + 0.5 * k1) | ||
| + | k3 = h * dvdt(t0 + 0.5 * h, v + 0.5 * k2) | ||
| + | k4 = h * dvdt(t0 + h, v + k3) | ||
| + | |||
| + | #next value of v | ||
| + | v = v + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4) | ||
| + | # Update next value of t | ||
| + | t0 = t0 + h | ||
| + | return v | ||
| + | # Driver method | ||
| + | t0 = 0 | ||
| + | v = 1 | ||
| + | t = 2 | ||
| + | h = 0.2 | ||
| + | print ('The value of y at x is:', rungeKutta(t0, v, t, h)) | ||
| + | |||
| + | |||
| + | |||
| + | C. Muasabah | ||
| + | |||
| + | https://youtu.be/xBV2l7Tj4MI | ||
| + | |||
| + | <comments voting="Plus" /> | ||
Latest revision as of 02:44, 28 October 2019
Contents
Tugas Mekanika Fluida
Biografi
Illiyyin Lafi Abrarri dengan NPM 1706070772 lahir di Surabaya, 23 Mei 1999 dari pasangan suami istri Amir Hamzah dan Dwi Riawati. Mengawali pendidikan mulai dari sekolah dasar hingga SMA di Surabaya. berasal dari SMAN 15 Surabaya dan melanjutkan pendidikan S1 di Teknik Mesin Universitas Indonesia. memiliki hobi bermain game, renang, dan badminton.
Karier
semua karir dimulai ketika masa perkuliahan dimulai dengan membantu tugas skripsi senior mengenai getaran pada tingkat awal, diikuti dengan mengikuti proyek desa Bungin yang diadakan oleh Prof Adi sejak 2018 hingga saat ini meski tidak terlalu berat, memulai mengajar anak SMA secara privat sejak tahun 2018 hingga saat ini, menjadi vice project officer ASUIFEST 2019, menjadi vice PIC Aeromodelling di MMENE sebuah event kebanggaan Ikatan mahasiswa Mesin, menjadi anggota student catalyst 2019 dan memenangkan best project tentang masalah ketidak toleransi umat beragama dan politik, menjadi anggota MPM FTUI periode 2019
PYTHON
Awal belajar sempat kaget karena selalu mengalami syntax error dan tidak mengetahui bagaimana caranya membuat line baru dibawah line sebelumnya. Ternyata tidak dimasukan nya fungsi yang benar. Hal yang sudah saya pelajari di python adalah mengenai operasi hitung tentang penambahan, pengurangan, pengalian, dan pembagian. Fungsi-fungsi persamaan yang sudah saya pelajari adalah
a = 4
b = a + 5
print (b)
9
dan seterusnya termasuk pengalian, pengurangan dan pembagian beberapa juga ada yang mengalami kesalah pahaman seperti
a = [2, 3, 4]
b = [1, 0, 3]
c = a + b
print(c)
[2, 1, 3, 0, 4, 3]
yang seharusnya diharapkan [3, 3, 7] ditambahlagi beberapa campuran kata dan angka akan menghasilkan eror karena tidak masuk akal dan tidak bias dilakukan operasi hitung matematika menggunakan fungsi Batasan angka seperti >, <, =, >=, dan <= memncoba program if, false, dan true dan membuat sebuah persamaan yang bias dihitung persamaan linear sederhana
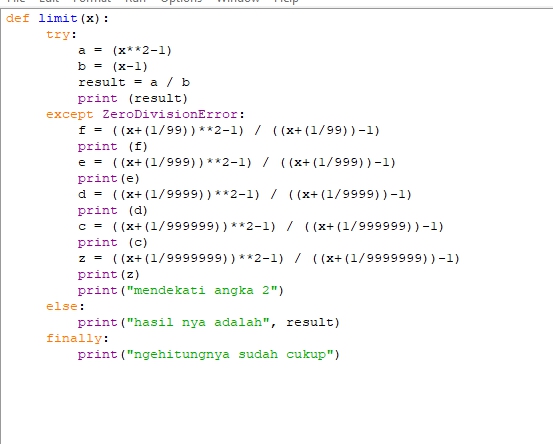
Hiburan metode numerik 1 A
Dalam mengerjakan soal (x^2-1)/(x-1) dengan x=1 tidak bisa mendapatkan hasil yang benar dikarenakan 0/0. Oleh sebab itu, saya gunakan limit pendekatan x=1. Soal dikerjakan dengan menambahkan perbedaan 1/9999999 yang mendekati angka nol sehingga hampir tidak merubah hasil dengan menggunakan module coding sebagai berikut
Pada module ini, saya memisahkan antara pembilang dan penyebut nya sehingga memudahkan perhitungan.
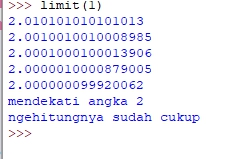
dan memiliki hasil seperti berikut
Hiburan metode numerik 1 B
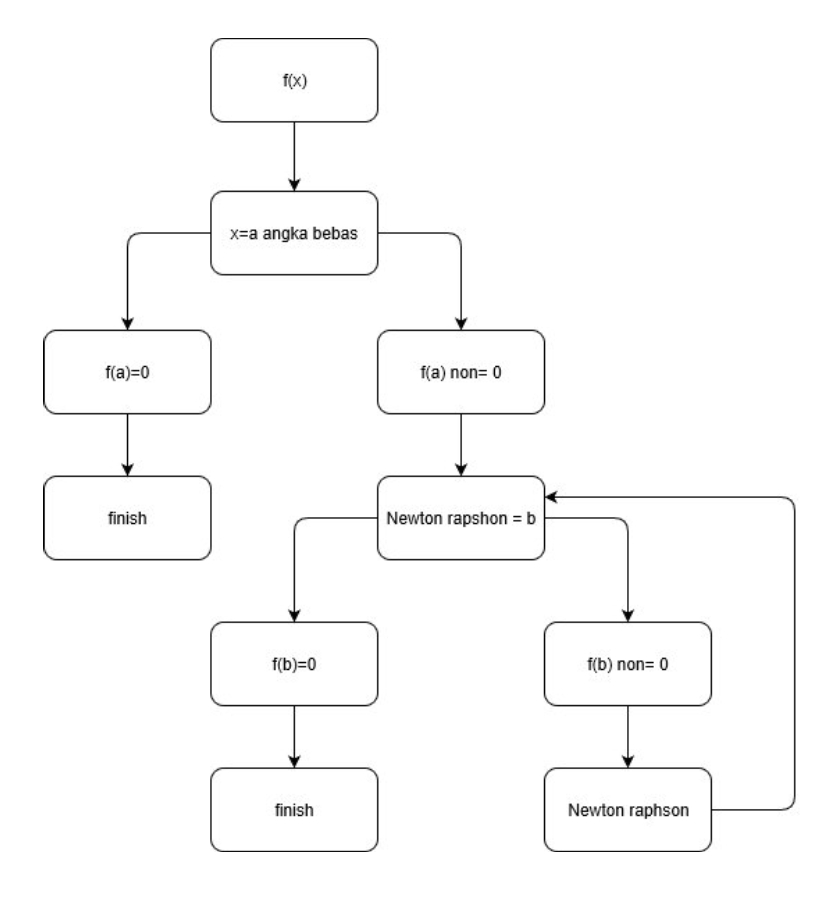
pada soal ini digunakan metode Newton Raphson sebagai metode mencari faktor dari persamaan tersebut
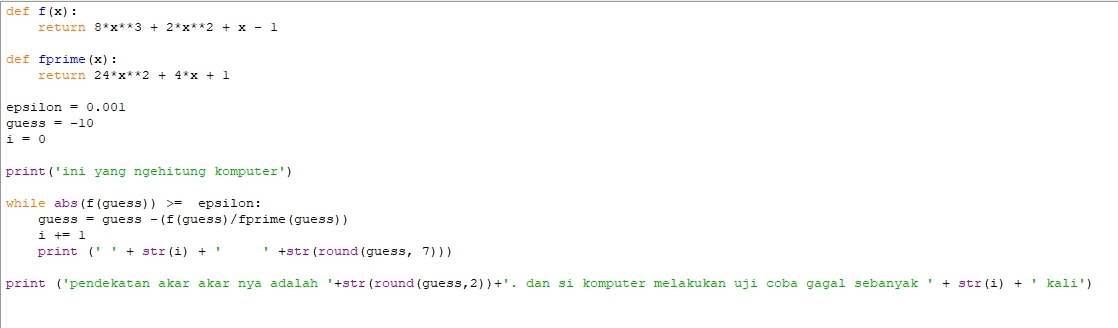
dengan module sebagai berikut
dan mendapatkan hasil sebagai berikut
dengan flowchart sebagai berikut
Hiburan 02- LAFI
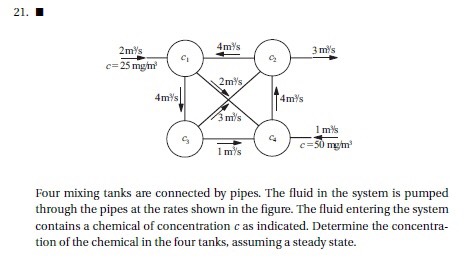
pada tugas hiburan ini
dikerjakan menggunakan hukum kontinuitas massa dimana masa yang masuk akan sama dengan yang dikeluarkan sehingga didapati rumus Q*p=Q*p sehingga akan mendapatakan 4 persamaan dengan 4 variabel
6C1 - 4C2 = 50
-2C1 - 1C3 + 4C4 = 50
7C2 - 3C3 - 4C4 = 0
-4C1 + 4C3 = 0
6C1 - 4C2 + 0C3 + 0C4 = 50
-2C1 + 0C2 - 1C3 + 4C4 = 50
0C1 + 7C2 - 3C3 - 4C4 = 0
-4C1 + 0C2 + 4C3 + 0C4 = 0
yang kemudian dijadikan dalam modue python lalu didapatkan nilai C1 = 275/9 , C2 = 100/3 , C3 = 275/9, C4 = 425/12
import numpy as np
class GEPP():
def __init__(self, A, b, doPricing=True):
#super(GEPP, self).__init__()
self.A = A # input: A is an n x n numpy matrix
self.b = b # b is an n x 1 numpy array
self.doPricing = doPricing
self.n = None # n is the length of A
self.x = None # x is the solution of Ax=b
self._validate_input() # method that validates input
self._elimination() # method that conducts elimination
self._backsub() # method that conducts back-substitution
def _validate_input(self):
self.n = len(self.A)
if self.b.size != self.n:
raise ValueError("Invalid argument: incompatible sizes between" +
"A & b.", self.b.size, self.n)
def _elimination(self):
"""
k represents the current pivot row. Since GE traverses the matrix in the
upper right triangle, we also use k for indicating the k-th diagonal
column index.
:return
"""
# Elimination
for k in range(self.n - 1):
if self.doPricing:
# Pivot
maxindex = abs(self.A[k:, k]).argmax() + k
if self.A[maxindex, k] == 0:
raise ValueError("Matrix is singular.")
# Swap
if maxindex != k:
self.Ak, maxindex = self.Amaxindex, k
self.bk, maxindex = self.bmaxindex, k
else:
if self.A[k, k] == 0:
raise ValueError("Pivot element is zero. Try setting doPricing to True.")
# Eliminate
for row in range(k + 1, self.n):
multiplier = self.A[row, k] / self.A[k, k]
self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:]
self.b[row] = self.b[row] - multiplier * self.b[k]
def _backsub(self):
# Back Substitution
self.x = np.zeros(self.n)
for k in range(self.n - 1, -1, -1):
self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k]
def main():
A = np.array([[6., -4., 0., 0.],
[-4., 0., 4., 0.],
[-2., 0., -1., 4.],
[0., 7., -3., -4.]])
b = np.array([[50.],
[0.],
[50.],
[0.]])
print("ini matriks awal nya")
print(A)
print("ini hasil yang awal")
print(b)
GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False)
print("ini hasil akhirnya")
print(GaussElimPiv.x)
print(GaussElimPiv.A)
print(GaussElimPiv.b)
GaussElimPiv = GEPP(A, b)
print(GaussElimPiv.x)
if __name__ == "__main__":
main()
quiz
1.
import numpy as np
class GEPP():
def __init__(self, A, b, doPricing=True):
self.A = A
self.b = b
self.doPricing = doPricing
self.n = None
self.x = None
self._validate_input()
self._elimination()
self._backsub()
def _validate_input(self):
self.n = len(self.A)
if self.b.size != self.n:
raise ValueError("yah bingung.", self.b.size, self.n)
def _elimination(self):
# Elimination
for k in range(self.n - 1):
if self.doPricing:
# Pivot
maxindex = abs(self.A[k:, k]).argmax() + k
if self.A[maxindex, k] == 0:
raise ValueError("Matrix ini singular.")
# Swap
if maxindex != k:
self.Ak, maxindex = self.Amaxindex, k
self.bk, maxindex = self.bmaxindex, k
else:
if self.A[k, k] == 0:
raise ValueError("coba lagi.")
# Eliminate
for row in range(k + 1, self.n):
multiplier = self.A[row, k] / self.A[k, k]
self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:]
self.b[row] = self.b[row] - multiplier * self.b[k]
def _backsub(self):
# Back Substitution
self.x = np.zeros(self.n)
for k in range(self.n - 1, -1, -1):
self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k]
def main():
A = np.array([[1., 2., 0., -2., 0.],
[0., 1., 0., 2., -1.],
[0., 1., -1., 1., -1.],
[0., 0., 2., 1., 2.],
[0., 0., 0., -1., 1.]])
b = np.array([[-4.],
[1.],
[-1.],
[1.],
[-2.]])
GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False)
print(GaussElimPiv.x)
print(GaussElimPiv.A)
print(GaussElimPiv.b)
GaussElimPiv = GEPP(A, b)
print(GaussElimPiv.x)
if __name__ == "__main__":
main()
#pada persamaan ke 3 dan ke 1 ditukar karena variabel awal tidak boleh bernilai nol
2.
import numpy as np from run_kut4 import * from printSoln import * from math import exp
x = 0.03
def F(x,y):
F = np.zeros(1)
F[0] = ((31/32)*exp(-4))+((1/4)*x**2)-(1/8)*x+(1/32)
return F
x = 0.0 xStop = 0.03 y = np.array([160]) h = 0.01 freq = 1
print(y)
X,Y = integrate(F,x,y,xStop,h)
printSoln(X,Y,freq)
input("\nPress return to exit")
UTS
A.
https://www.youtube.com/watch?v=Lar9ahvi2ew
import numpy as np
class GEPP():
def __init__(self, A, b, doPricing=True):
#super(GEPP, self).__init__()
self.A = A # input: A is an n x n numpy matrix
self.b = b # b is an n x 1 numpy array
self.doPricing = doPricing
self.n = None # n is the length of A
self.x = None # x is the solution of Ax=b
self._validate_input() # method that validates input
self._elimination() # method that conducts elimination
self._backsub() # method that conducts back-substitution
def _validate_input(self):
self.n = len(self.A)
if self.b.size != self.n:
raise ValueError("Invalid argument: incompatible sizes between" +
"A & b.", self.b.size, self.n)
def _elimination(self):
"""
k represents the current pivot row. Since GE traverses the matrix in the
upper right triangle, we also use k for indicating the k-th diagonal
column index.
:return
"""
# Elimination
for k in range(self.n - 1):
if self.doPricing:
# Pivot
maxindex = abs(self.A[k:, k]).argmax() + k
if self.A[maxindex, k] == 0:
raise ValueError("Matrix is singular.")
# Swap
if maxindex != k:
self.Ak, maxindex = self.Amaxindex, k
self.bk, maxindex = self.bmaxindex, k
else:
if self.A[k, k] == 0:
raise ValueError("Pivot element is zero. Try setting doPricing to True.")
# Eliminate
for row in range(k + 1, self.n):
multiplier = self.A[row, k] / self.A[k, k]
self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:]
self.b[row] = self.b[row] - multiplier * self.b[k]
def _backsub(self):
# Back Substitution
self.x = np.zeros(self.n)
for k in range(self.n - 1, -1, -1):
self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k]
def main():
A = np.array([[1., 0., 0., 0.],
[-1., 1., 0., 0.],
[0., 0., -1., 1.],
[0., 0., 0., 1.]])
b = np.array([[50.],
[20.],
[5.],
[10.]])
GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False)
print(GaussElimPiv.x)
print(GaussElimPiv.A)
print(GaussElimPiv.b)
GaussElimPiv = GEPP(A, b)
print(GaussElimPiv.x)
if __name__ == "__main__":
main()
B.
dengan asumsi percepatan mobil sebesar 10m/s**2
perlambatan gesek jalan sebesar 2m/s**2
dan perlambatan karena gesek udara yang dipengaruhi oleh kecepatan 0,001*v
https://www.youtube.com/watch?v=ystTyu-qooA
import numpy as np
# Python program to implement Runge Kutta method # with acceleration of car is 10 m/s**2 # air friction and road friction is -0.001*V m/s and -2m/s**2 # so equation became v = 10*t - 2*t - 0.001*v # A sample differential equation "dv / dt = 8/1.001"
def dvdt(t,v):
return (8/1.001)
# Finds value of y for a given x using step size h
# and initial value y0 at x0.
def rungeKutta(t0, v0, t, h):
#count number of step size
#step h
n = (int)((t - t0)/h)
v = v0
for i in range (1, n + 1):
"apply rungakutta"
k1 = h * dvdt(t0, v)
k2 = h * dvdt(t0 + 0.5 * h, v + 0.5 * k1)
k3 = h * dvdt(t0 + 0.5 * h, v + 0.5 * k2)
k4 = h * dvdt(t0 + h, v + k3)
#next value of v
v = v + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)
# Update next value of t
t0 = t0 + h
return v
# Driver method
t0 = 0
v = 1
t = 2
h = 0.2
print ('The value of y at x is:', rungeKutta(t0, v, t, h))
C. Muasabah

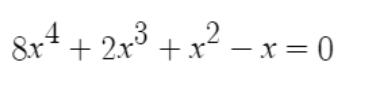


Enable comment auto-refresher
Bagus fadhlurrohman
Permalink |
Anonymous user #1
Permalink |
Geraldositorus
Anggitoz
Permalink |
Edosyafei
Permalink |
IlliyyinLafi
Ahmadsennop
Permalink |