Difference between revisions of "Rizky Narendra Putra"
| (41 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | Profil: | ||
| + | Rizky Narendra Putra / 1606907524 | ||
| + | Teknik Mesin Universitas Indonesia | ||
| + | [[File:Muka.jpg]] | ||
| + | ---- | ||
| + | |||
[[File:Studi Kasus Bab 8 Rizky.jpg]] | [[File:Studi Kasus Bab 8 Rizky.jpg]] | ||
[[File:Studi Kasus Bab 9 Rizky.jpg]] | [[File:Studi Kasus Bab 9 Rizky.jpg]] | ||
[[File:Studi Kasus Bab 10 Rizky.jpg]] | [[File:Studi Kasus Bab 10 Rizky.jpg]] | ||
[[File:Studi Kasus Bab 11 Rizky.jpg]] | [[File:Studi Kasus Bab 11 Rizky.jpg]] | ||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | Video Mekanika Fluida Bab 8: https://www.youtube.com/watch?v=42tyCDgc2dA&feature=youtu.be | ||
| + | |||
| + | Video Mekanika Fluida Bab 9: https://www.youtube.com/watch?v=sDhnzQfGJoU&feature=youtu.be | ||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| + | Tugas 1 Kelas Metode Numerik: | ||
| + | |||
| + | Apa yang saya pelajari tentang Python: | ||
| + | |||
| + | Python merupakan bahasa pemograman | ||
| + | Python dapat mengerjakan operasi matematika ( integral, penjumlahan, pengurangan, pengalian, pangkat, pembagian, dst ) | ||
| + | Jika dalam suatu pembagian hasilnya ada desimal dan kita tidak ingin memperlihatkan desimal tersebut, kita dapat menggunakan rumus misal: 5//2, maka akan keluar hasilnya 2, bukan 2,5 | ||
| + | dengan menggunakan // maka desimal dalam pembagian tersebut akan hilang, namun jika kita ingin memperlihatkan desimal tersebut, cukup: 5/2, maka akan keluar hasilnya 2,5 | ||
| + | Jika kita ingin menggunakan pangkat, maka dapat dilakukan 2**5 dan hasilnya akan keluar 32, jika kita ingin perkalian saja maka dapat digunakan 2*5 dan akan keluar hasilnya 10 | ||
| + | |||
| + | Untuk operasi matematika, python mempunyai prioritas tertinggi sampai yang terendah yaitu: | ||
| + | 1. ( .. ) | ||
| + | 2. ( * , / , ** ) | ||
| + | 3. ( +,- ) | ||
| + | |||
| + | ---- | ||
| + | Tugas 2 Metode Numerik | ||
| + | |||
| + | [[File:program python limit.png]] | ||
| + | [[File:hasil program python limit.png]] | ||
| + | |||
| + | ---- | ||
| + | |||
| + | Tugas 3 | ||
| + | |||
| + | Menggunakan matrix equation untuk eliminasi menggunakan Gaussian Elimination. | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | 6x<sub>1</sub> + 4x<sub>2</sub> = 50 | ||
| + | 2x<sub>1</sub> + x<sub>3</sub> + 4x<sub>4</sub> = 50 | ||
| + | 7x<sub>2</sub> + 3x<sub>3</sub> + 4x<sub>4</sub> = 50 | ||
| + | 4x<sub>1</sub> + 4x<sub>3</sub> = 50 | ||
| + | |||
| + | Didapat hasil matrix: | ||
| + | [[6. 4. 0. 0.] | ||
| + | [2. 0. 1. 4.] | ||
| + | [0. 7. 3. 4.] | ||
| + | [4. 0. 4. 0.]] | ||
| + | </div> | ||
| + | |||
| + | Mendefinisikan matrix di dalam python: | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | import numpy as np | ||
| + | <br>A = np.array([[6, 4, 0, 0], [2, 0 ,1, 4], [0, 7, 3, 4], [ 4, 0, 4, 0]], float) | ||
| + | B = np.array([50, 50, 0, 0], float) | ||
| + | <br>n = len(A) | ||
| + | </div> | ||
| + | |||
| + | Menggunakan Eliminasi Gaussian | ||
| + | |||
| + | <div border-style: inset;"> | ||
| + | for k in range(0,n-1): | ||
| + | for i in range(k+1,n): | ||
| + | if A[i,k]!=0 : | ||
| + | lam = A[i,k]/A[k,k] | ||
| + | A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam) | ||
| + | B[i] = B[i]-(B[k]*lam) | ||
| + | x = np.zeros(n,float) | ||
| + | for m in range(n-1,-1,-1): | ||
| + | x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m] | ||
| + | </div> | ||
| + | |||
| + | ---- | ||
| + | KUIS 1 METNUM : | ||
| + | |||
| + | soal nomer 1 runge kutta: | ||
| + | kode: | ||
| + | |||
| + | import numpy as np | ||
| + | def diff_y (x,y) : | ||
| + | fungsi = x**2 - 4*y | ||
| + | return (fungsi) | ||
| + | x = 0 | ||
| + | y = 1 | ||
| + | h = 0.01 | ||
| + | step_size = np.arrange (0,0.03,h) | ||
| + | for t in step_size: | ||
| + | k1 = diff_y (x,y) | ||
| + | k2 = diff_y ((x+0.5*h),(y+0.5*k1*h)) | ||
| + | |||
| + | y = y+k1*h | ||
| + | |||
| + | print ('nilai y(0,03) adalah',y) | ||
| + | |||
| + | Hasil: | ||
| + | |||
| + | Soal nomer 2 Gaussian elimination method | ||
| + | Kode: | ||
| + | |||
| + | import numpy as np | ||
| + | |||
| + | |||
| + | class GEPP(): | ||
| + | |||
| + | def __init__(self, A, b, doPricing=True): | ||
| + | #super(GEPP, self).__init__() | ||
| + | |||
| + | self.A = A # input: A is an n x n numpy matrix | ||
| + | self.b = b # b is an n x 1 numpy array | ||
| + | self.doPricing = doPricing | ||
| + | |||
| + | self.n = None # n is the length of A | ||
| + | self.x = None # x is the solution of Ax=b | ||
| + | |||
| + | self._validate_input() # method that validates input | ||
| + | self._elimination() # method that conducts elimination | ||
| + | self._backsub() # method that conducts back-substitution | ||
| + | |||
| + | def _validate_input(self): | ||
| + | self.n = len(self.A) | ||
| + | if self.b.size != self.n: | ||
| + | raise ValueError("Invalid argument: incompatible sizes between" + | ||
| + | "A & b.", self.b.size, self.n) | ||
| + | |||
| + | def _elimination(self): | ||
| + | |||
| + | |||
| + | # Elimination | ||
| + | for k in range(self.n - 1): | ||
| + | if self.doPricing: | ||
| + | # Pivot | ||
| + | maxindex = abs(self.A[k:, k]).argmax() + k | ||
| + | if self.A[maxindex, k] == 0: | ||
| + | raise ValueError("Matrix is singular.") | ||
| + | # Swap | ||
| + | if maxindex != k: | ||
| + | self.A[[k, maxindex]] = self.A[[maxindex, k]] | ||
| + | self.b[[k, maxindex]] = self.b[[maxindex, k]] | ||
| + | else: | ||
| + | if self.A[k, k] == 0: | ||
| + | raise ValueError("Pivot element is zero. Try setting doPricing to True.") | ||
| + | # Eliminate | ||
| + | for row in range(k + 1, self.n): | ||
| + | multiplier = self.A[row, k] / self.A[k, k] | ||
| + | self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:] | ||
| + | self.b[row] = self.b[row] - multiplier * self.b[k] | ||
| + | |||
| + | def _backsub(self): | ||
| + | # Back Substitution | ||
| + | |||
| + | self.x = np.zeros(self.n) | ||
| + | for k in range(self.n - 1, -1, -1): | ||
| + | self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k] | ||
| + | |||
| + | |||
| + | def main(): | ||
| + | A = np.array([[1., 2., 0., -2., 0.], | ||
| + | [0., 1., 0., 2., -1.], | ||
| + | [0., 0., 2., 1., 2.], | ||
| + | [0., 0., 0., -1., 1.], | ||
| + | [0., 1., -1., 1., -1.]]) | ||
| + | b = np.array([[-4.], | ||
| + | [1.], | ||
| + | [1.], | ||
| + | [-2.], | ||
| + | [-1.]]) | ||
| + | GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False) | ||
| + | print(GaussElimPiv.x) | ||
| + | print(GaussElimPiv.A) | ||
| + | print(GaussElimPiv.b) | ||
| + | GaussElimPiv = GEPP(A, b) | ||
| + | print(GaussElimPiv.x) | ||
| + | |||
| + | if __name__ == "__main__": | ||
| + | main() | ||
| + | |||
| + | Hasil: [[File:hasil ss.png]] | ||
| + | |||
| + | ---- | ||
| + | UTS METODE NUMERIK 2019 | ||
| + | |||
| + | Video Muasabah Diri: https://www.youtube.com/watch?v=jkp6N7AG6_g | ||
| + | |||
| + | Soal B: | ||
| + | |||
| + | import numpy as np | ||
| + | def diff_y (x,y): | ||
| + | fungsi = x**2 - 2*y | ||
| + | return (fungsi) | ||
| + | x=0 | ||
| + | y=10 | ||
| + | h=10 | ||
| + | a = 2 | ||
| + | j = 1 | ||
| + | step_size = -np.arange (0,2,h) | ||
| + | for t in step_size: | ||
| + | k1 = diff_y (x,y) - (a + j) | ||
| + | k2 = diff_y ((x+0.5*h),(y+0.05*k1*h)) - (a + j) | ||
| + | |||
| + | w1 = y + 1/3*(k1+2*k2) | ||
| + | print ('maka x(2) adalah', w1) | ||
| + | |||
| + | a = hambatan angin | ||
| + | j = gesekan jalan | ||
| + | |||
| + | [[File:Hasil UTS 2019 ss.jpg]] | ||
| + | Video Penjelasan: https://www.youtube.com/watch?v=TAMz5momeSc | ||
| + | |||
| + | Soal A: | ||
| + | |||
| + | print ('Penghitungan Soal UTS A') | ||
| + | import numpy as np | ||
| + | class GEPP(): | ||
| + | def __init__(self, A, b, doPricing=True): | ||
| + | #super(GEPP, self).__init__() | ||
| + | self.A = A # input: A is an n x n numpy matrix | ||
| + | self.b = b # b is an n x 1 numpy array | ||
| + | self.doPricing = doPricing | ||
| + | |||
| + | self.n = None # n is the length of A | ||
| + | self.x = None # x is the solution of Ax=b | ||
| + | |||
| + | self._validate_input() # method that validates input | ||
| + | self._elimination() # method that conducts elimination | ||
| + | self._backsub() # method that conducts back-substitution | ||
| + | |||
| + | def _validate_input(self): | ||
| + | self.n = len(self.A) | ||
| + | if self.b.size != self.n: | ||
| + | raise ValueError("Invalid argument: incompatible sizes between" + | ||
| + | "A & b.", self.b.size, self.n) | ||
| + | |||
| + | def _elimination(self): | ||
| + | """ | ||
| + | k represents the current pivot row. Since GE traverses the matrix in the | ||
| + | upper right triangle, we also use k for indicating the k-th diagonal | ||
| + | column index. | ||
| + | :return | ||
| + | """ | ||
| + | # Elimination | ||
| + | for k in range(self.n - 1): | ||
| + | if self.doPricing: | ||
| + | # Pivot | ||
| + | maxindex = abs(self.A[k:, k]).argmax() + k | ||
| + | if self.A[maxindex, k] == 0: | ||
| + | raise ValueError("Matrix is singular.") | ||
| + | # Swap | ||
| + | if maxindex != k: | ||
| + | self.Ak, maxindex = self.Amaxindex, k | ||
| + | self.bk, maxindex = self.bmaxindex, k | ||
| + | else: | ||
| + | if self.A[k, k] == 0: | ||
| + | raise ValueError("Pivot element is zero. Try setting doPricing to True.") | ||
| + | # Eliminate | ||
| + | for row in range(k + 1, self.n): | ||
| + | multiplier = self.A[row, k] / self.A[k, k] | ||
| + | self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:] | ||
| + | self.b[row] = self.b[row] - multiplier * self.b[k] | ||
| + | |||
| + | def _backsub(self): | ||
| + | # Back Substitution | ||
| + | self.x = np.zeros(self.n) | ||
| + | for k in range(self.n - 1, -1, -1): | ||
| + | self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k] | ||
| + | |||
| + | def main(): | ||
| + | A = np.array([[1., 0., 0., 0.], | ||
| + | [-1., 1., 0., 0.], | ||
| + | [0., 0., -1., 1.], | ||
| + | [0., 0., 0., 1.]]) | ||
| + | b = np.array([[50.], | ||
| + | [20.], | ||
| + | [5.], | ||
| + | [10.]]) | ||
| + | GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False) | ||
| + | print(GaussElimPiv.x) | ||
| + | print(GaussElimPiv.A) | ||
| + | print(GaussElimPiv.b) | ||
| + | GaussElimPiv = GEPP(A, b) | ||
| + | print(GaussElimPiv.x) | ||
| + | if __name__ == "__main__": | ||
| + | main() | ||
| + | |||
| + | [[File:utsmetnum.jpeg]] | ||
| + | |||
| + | Video Penjelasan: https://www.youtube.com/watch?v=6SqbgmkvWQc | ||
Latest revision as of 00:28, 28 October 2019
Profil:
Rizky Narendra Putra / 1606907524
Teknik Mesin Universitas Indonesia

Video Mekanika Fluida Bab 8: https://www.youtube.com/watch?v=42tyCDgc2dA&feature=youtu.be
Video Mekanika Fluida Bab 9: https://www.youtube.com/watch?v=sDhnzQfGJoU&feature=youtu.be
Tugas 1 Kelas Metode Numerik:
Apa yang saya pelajari tentang Python:
Python merupakan bahasa pemograman Python dapat mengerjakan operasi matematika ( integral, penjumlahan, pengurangan, pengalian, pangkat, pembagian, dst ) Jika dalam suatu pembagian hasilnya ada desimal dan kita tidak ingin memperlihatkan desimal tersebut, kita dapat menggunakan rumus misal: 5//2, maka akan keluar hasilnya 2, bukan 2,5 dengan menggunakan // maka desimal dalam pembagian tersebut akan hilang, namun jika kita ingin memperlihatkan desimal tersebut, cukup: 5/2, maka akan keluar hasilnya 2,5 Jika kita ingin menggunakan pangkat, maka dapat dilakukan 2**5 dan hasilnya akan keluar 32, jika kita ingin perkalian saja maka dapat digunakan 2*5 dan akan keluar hasilnya 10
Untuk operasi matematika, python mempunyai prioritas tertinggi sampai yang terendah yaitu: 1. ( .. ) 2. ( * , / , ** ) 3. ( +,- )
Tugas 2 Metode Numerik
Tugas 3
Menggunakan matrix equation untuk eliminasi menggunakan Gaussian Elimination.
6x1 + 4x2 = 50 2x1 + x3 + 4x4 = 50 7x2 + 3x3 + 4x4 = 50 4x1 + 4x3 = 50
Didapat hasil matrix:
[[6. 4. 0. 0.] [2. 0. 1. 4.] [0. 7. 3. 4.] [4. 0. 4. 0.]]
Mendefinisikan matrix di dalam python:
import numpy as np
A = np.array([[6, 4, 0, 0], [2, 0 ,1, 4], [0, 7, 3, 4], [ 4, 0, 4, 0]], float) B = np.array([50, 50, 0, 0], float)
n = len(A)
Menggunakan Eliminasi Gaussian
for k in range(0,n-1):
for i in range(k+1,n):
if A[i,k]!=0 :
lam = A[i,k]/A[k,k]
A[i,k:n] = A[i,k:n]-(A[k,k:n]*lam)
B[i] = B[i]-(B[k]*lam)
x = np.zeros(n,float)
for m in range(n-1,-1,-1):
x[m]=(B[m]-np.dot(A[m,m+1:n],x[m+1:n]))/A[m,m]
KUIS 1 METNUM :
soal nomer 1 runge kutta: kode:
import numpy as np def diff_y (x,y) :
fungsi = x**2 - 4*y return (fungsi)
x = 0 y = 1 h = 0.01 step_size = np.arrange (0,0.03,h) for t in step_size:
k1 = diff_y (x,y) k2 = diff_y ((x+0.5*h),(y+0.5*k1*h))
y = y+k1*h
print ('nilai y(0,03) adalah',y)
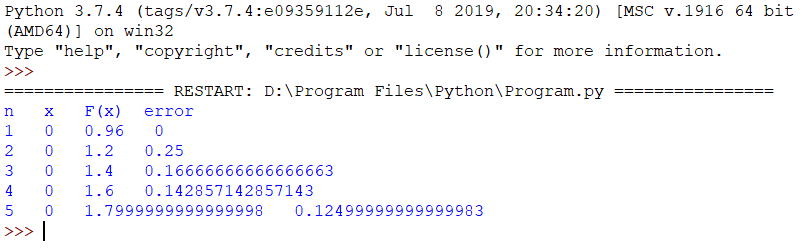
Hasil:
Soal nomer 2 Gaussian elimination method Kode:
import numpy as np
class GEPP():
def __init__(self, A, b, doPricing=True):
#super(GEPP, self).__init__()
self.A = A # input: A is an n x n numpy matrix
self.b = b # b is an n x 1 numpy array
self.doPricing = doPricing
self.n = None # n is the length of A
self.x = None # x is the solution of Ax=b
self._validate_input() # method that validates input
self._elimination() # method that conducts elimination
self._backsub() # method that conducts back-substitution
def _validate_input(self):
self.n = len(self.A)
if self.b.size != self.n:
raise ValueError("Invalid argument: incompatible sizes between" +
"A & b.", self.b.size, self.n)
def _elimination(self):
# Elimination
for k in range(self.n - 1):
if self.doPricing:
# Pivot
maxindex = abs(self.A[k:, k]).argmax() + k
if self.A[maxindex, k] == 0:
raise ValueError("Matrix is singular.")
# Swap
if maxindex != k:
self.Ak, maxindex = self.Amaxindex, k
self.bk, maxindex = self.bmaxindex, k
else:
if self.A[k, k] == 0:
raise ValueError("Pivot element is zero. Try setting doPricing to True.")
# Eliminate
for row in range(k + 1, self.n):
multiplier = self.A[row, k] / self.A[k, k]
self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:]
self.b[row] = self.b[row] - multiplier * self.b[k]
def _backsub(self):
# Back Substitution
self.x = np.zeros(self.n)
for k in range(self.n - 1, -1, -1):
self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k]
def main():
A = np.array([[1., 2., 0., -2., 0.],
[0., 1., 0., 2., -1.],
[0., 0., 2., 1., 2.],
[0., 0., 0., -1., 1.],
[0., 1., -1., 1., -1.]])
b = np.array([[-4.],
[1.],
[1.],
[-2.],
[-1.]])
GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False)
print(GaussElimPiv.x)
print(GaussElimPiv.A)
print(GaussElimPiv.b)
GaussElimPiv = GEPP(A, b)
print(GaussElimPiv.x)
if __name__ == "__main__":
main()
UTS METODE NUMERIK 2019
Video Muasabah Diri: https://www.youtube.com/watch?v=jkp6N7AG6_g
Soal B:
import numpy as np def diff_y (x,y):
fungsi = x**2 - 2*y return (fungsi)
x=0 y=10 h=10 a = 2 j = 1 step_size = -np.arange (0,2,h) for t in step_size:
k1 = diff_y (x,y) - (a + j) k2 = diff_y ((x+0.5*h),(y+0.05*k1*h)) - (a + j)
w1 = y + 1/3*(k1+2*k2) print ('maka x(2) adalah', w1)
a = hambatan angin j = gesekan jalan
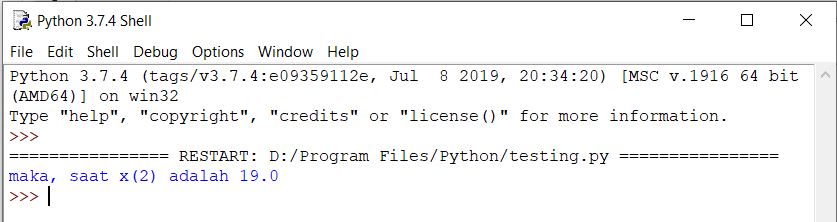 Video Penjelasan: https://www.youtube.com/watch?v=TAMz5momeSc
Video Penjelasan: https://www.youtube.com/watch?v=TAMz5momeSc
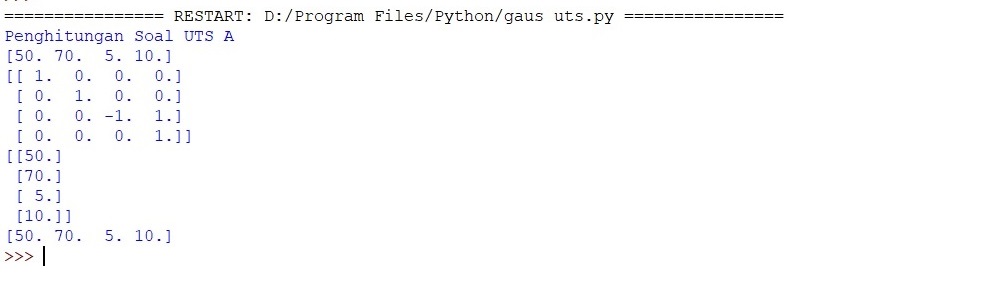
Soal A:
print ('Penghitungan Soal UTS A') import numpy as np class GEPP():
def __init__(self, A, b, doPricing=True):
#super(GEPP, self).__init__()
self.A = A # input: A is an n x n numpy matrix
self.b = b # b is an n x 1 numpy array
self.doPricing = doPricing
self.n = None # n is the length of A
self.x = None # x is the solution of Ax=b
self._validate_input() # method that validates input
self._elimination() # method that conducts elimination
self._backsub() # method that conducts back-substitution
def _validate_input(self):
self.n = len(self.A)
if self.b.size != self.n:
raise ValueError("Invalid argument: incompatible sizes between" +
"A & b.", self.b.size, self.n)
def _elimination(self):
"""
k represents the current pivot row. Since GE traverses the matrix in the
upper right triangle, we also use k for indicating the k-th diagonal
column index.
:return
"""
# Elimination
for k in range(self.n - 1):
if self.doPricing:
# Pivot
maxindex = abs(self.A[k:, k]).argmax() + k
if self.A[maxindex, k] == 0:
raise ValueError("Matrix is singular.")
# Swap
if maxindex != k:
self.Ak, maxindex = self.Amaxindex, k
self.bk, maxindex = self.bmaxindex, k
else:
if self.A[k, k] == 0:
raise ValueError("Pivot element is zero. Try setting doPricing to True.")
# Eliminate
for row in range(k + 1, self.n):
multiplier = self.A[row, k] / self.A[k, k]
self.A[row, k:] = self.A[row, k:] - multiplier * self.A[k, k:]
self.b[row] = self.b[row] - multiplier * self.b[k]
def _backsub(self):
# Back Substitution
self.x = np.zeros(self.n)
for k in range(self.n - 1, -1, -1):
self.x[k] = (self.b[k] - np.dot(self.A[k, k + 1:], self.x[k + 1:])) / self.A[k, k]
def main():
A = np.array([[1., 0., 0., 0.],
[-1., 1., 0., 0.],
[0., 0., -1., 1.],
[0., 0., 0., 1.]])
b = np.array([[50.],
[20.],
[5.],
[10.]])
GaussElimPiv = GEPP(np.copy(A), np.copy(b), doPricing=False)
print(GaussElimPiv.x)
print(GaussElimPiv.A)
print(GaussElimPiv.b)
GaussElimPiv = GEPP(A, b)
print(GaussElimPiv.x)
if __name__ == "__main__":
main()
Video Penjelasan: https://www.youtube.com/watch?v=6SqbgmkvWQc