Difference between revisions of "Algoritma python untuk kuis"
| Line 2: | Line 2: | ||
[[File:Soal_2.1_no_6.JPG|500px|thumb|left]] | [[File:Soal_2.1_no_6.JPG|500px|thumb|left]] | ||
| − | Coding Python untuk penyelesaian soal diatas sebagai berkut : | + | |
| − | [[File:Algoritma_1.JPG|1000px|thumb|left]] | + | |
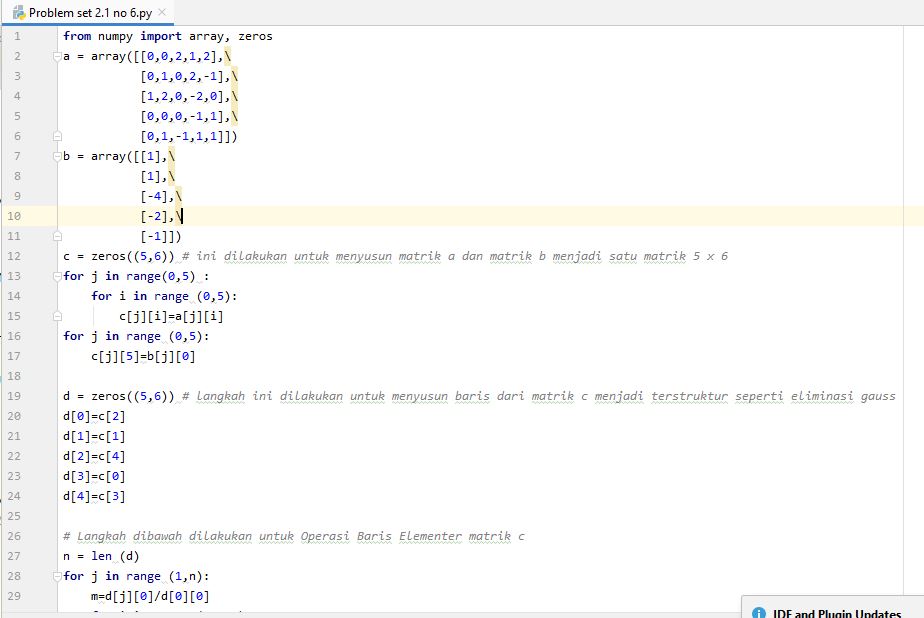
| − | [[File:Algoritma_2.JPG|1000px|thumb|left]] | + | Coding Python untuk penyelesaian soal diatas sebagai berkut : |
| − | [[File:Algoritma_3.JPG|1000px|thumb|left]] | + | [[File:Algoritma_1.JPG|1000px|thumb|left]] |
| + | [[File:Algoritma_2.JPG|1000px|thumb|left]] | ||
| + | [[File:Algoritma_3.JPG|1000px|thumb|left]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Berikut ini adalah algoritmanya : | ||
| + | from numpy import array, zeros | ||
| + | a = array([[0,0,2,1,2],\ | ||
| + | [0,1,0,2,-1],\ | ||
| + | [1,2,0,-2,0],\ | ||
| + | [0,0,0,-1,1],\ | ||
| + | [0,1,-1,1,1]]) | ||
| + | b = array([[1],\ | ||
| + | [1],\ | ||
| + | [-4],\ | ||
| + | [-2],\ | ||
| + | [-1]]) | ||
| + | c = zeros((5,6)) # ini dilakukan untuk menyusun matrik a dan matrik b menjadi satu matrik 5 x 6 | ||
| + | for j in range(0,5) : | ||
| + | for i in range (0,5): | ||
| + | c[j][i]=a[j][i] | ||
| + | for j in range (0,5): | ||
| + | c[j][5]=b[j][0] | ||
| + | |||
| + | d = zeros((5,6)) # langkah ini dilakukan untuk menyusun baris dari matrik c menjadi terstruktur seperti eliminasi gauss | ||
| + | d[0]=c[2] | ||
| + | d[1]=c[1] | ||
| + | d[2]=c[4] | ||
| + | d[3]=c[0] | ||
| + | d[4]=c[3] | ||
| + | |||
| + | # Langkah dibawah dilakukan untuk Operasi Baris Elementer matrik c | ||
| + | n = len (d) | ||
| + | for j in range (1,n): | ||
| + | m=d[j][0]/d[0][0] | ||
| + | for i in range (0,n+1): | ||
| + | d[j][i]=d[j][i]-m*d[0][i] | ||
| + | for j in range(2, n): | ||
| + | m = d[j][1]/d[1][1] | ||
| + | for i in range(1,n+1): | ||
| + | d[j][i]=d[j][i]-m*d[1][i] | ||
| + | for j in range(3, n): | ||
| + | m = d[j][2]/d[2][2] | ||
| + | for i in range(1,n+1): | ||
| + | d[j][i]=d[j][i]-m*d[2][i] | ||
| + | for j in range(4,n): | ||
| + | m = d[j][3]/d[3][3] | ||
| + | for i in range(1,n+1): | ||
| + | d[j][i]=d[j][i]-m*d[3][i] | ||
| + | |||
| + | # Langkah dibawah dilakukan untuk back substitution demi mendapatkan hasil x1, x2. x3, x4, dan x5 | ||
| + | X = zeros((n, 1)) | ||
| + | X[n - 1][0] = d[n-1][n]/d[n-1][n-1] | ||
| + | for j in range(n-2,-1,-1): | ||
| + | S=0 | ||
| + | for i in range(j+1,n): | ||
| + | S = S + d[j][i]*X[i][0] | ||
| + | X[j][0] = (d[j][n]-S)/d[j][j] | ||
| + | |||
| + | print(X) | ||
Revision as of 13:21, 17 October 2019
Problem set 2.1 no 6 hal 55 (buku "Numerical Methods in Engineering with Python 3")
Coding Python untuk penyelesaian soal diatas sebagai berkut :
Berikut ini adalah algoritmanya :
from numpy import array, zeros
a = array([[0,0,2,1,2],\
[0,1,0,2,-1],\
[1,2,0,-2,0],\
[0,0,0,-1,1],\
[0,1,-1,1,1]])
b = array([[1],\
[1],\
[-4],\
[-2],\
[-1]])
c = zeros((5,6)) # ini dilakukan untuk menyusun matrik a dan matrik b menjadi satu matrik 5 x 6
for j in range(0,5) :
for i in range (0,5):
c[j][i]=a[j][i]
for j in range (0,5):
c[j][5]=b[j][0]
d = zeros((5,6)) # langkah ini dilakukan untuk menyusun baris dari matrik c menjadi terstruktur seperti eliminasi gauss d[0]=c[2] d[1]=c[1] d[2]=c[4] d[3]=c[0] d[4]=c[3]
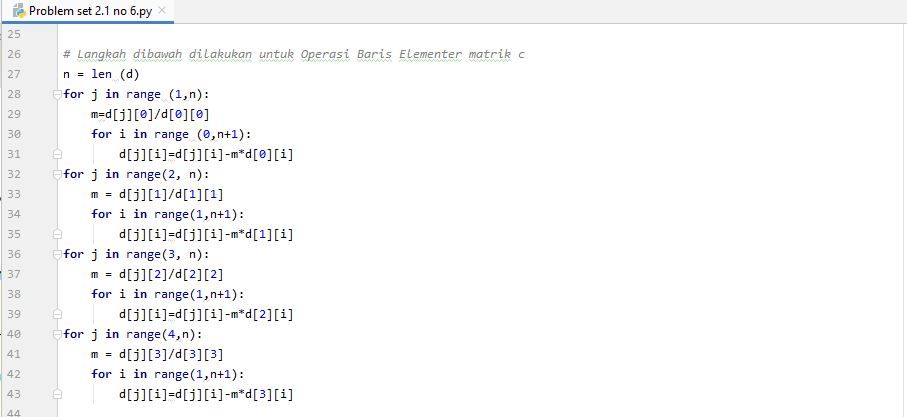
# Langkah dibawah dilakukan untuk Operasi Baris Elementer matrik c
n = len (d)
for j in range (1,n):
m=d[j][0]/d[0][0]
for i in range (0,n+1):
d[j][i]=d[j][i]-m*d[0][i]
for j in range(2, n):
m = d[j][1]/d[1][1]
for i in range(1,n+1):
d[j][i]=d[j][i]-m*d[1][i]
for j in range(3, n):
m = d[j][2]/d[2][2]
for i in range(1,n+1):
d[j][i]=d[j][i]-m*d[2][i]
for j in range(4,n):
m = d[j][3]/d[3][3]
for i in range(1,n+1):
d[j][i]=d[j][i]-m*d[3][i]
# Langkah dibawah dilakukan untuk back substitution demi mendapatkan hasil x1, x2. x3, x4, dan x5
X = zeros((n, 1))
X[n - 1][0] = d[n-1][n]/d[n-1][n-1]
for j in range(n-2,-1,-1):
S=0
for i in range(j+1,n):
S = S + d[j][i]*X[i][0]
X[j][0] = (d[j][n]-S)/d[j][j]
print(X)