Difference between revisions of "TURUNAN NUMERIK"
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
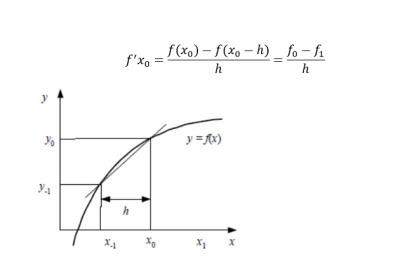
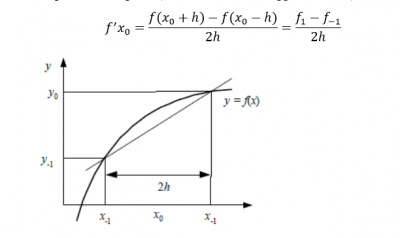
Pada dasarnya turunan dibedakan menjadi 3 yakni maju, mundur dan pusat. Pada nilai yang sama, turunan numerik pada jenis pusat merupakan turunan paling baik, dengan keberlanjutan maju dan mundur sebagai keakuratan yang sama. Akan tetapi, hal tersebut juga dipngaruhi oleh nilai h sebagai pengaruh terhadap truncation error. Berikut merupakan formula dan gambar grafik dari masing-masing jenis: | Pada dasarnya turunan dibedakan menjadi 3 yakni maju, mundur dan pusat. Pada nilai yang sama, turunan numerik pada jenis pusat merupakan turunan paling baik, dengan keberlanjutan maju dan mundur sebagai keakuratan yang sama. Akan tetapi, hal tersebut juga dipngaruhi oleh nilai h sebagai pengaruh terhadap truncation error. Berikut merupakan formula dan gambar grafik dari masing-masing jenis: | ||
| − | 1. Turunan Hampiran Maju | + | '''1. Turunan Hampiran Maju''' |
| − | [[File:MAJU.PNG]] | + | [[File:MAJU.PNG|400px|]] |
| + | '''2. Turunan Hampiran Mundur''' | ||
| + | [[File:MUNDUR.PNG|400px|]] | ||
| + | '''2. Turunan Hampiran Pusat''' | ||
| + | |||
| + | [[File:PUSAT.PNG|400px|]] | ||
| + | |||
| + | |||
| + | Dengan menggunakan formula inilah, kita dapat menemukan hampiran nilai H. Sehingga turunan numerik dapat dilakukan | ||
Kembali ke Halaman Awal Rilvan: | Kembali ke Halaman Awal Rilvan: | ||
[[M. Rilvan Adinugraha]] | [[M. Rilvan Adinugraha]] | ||
Latest revision as of 10:25, 24 September 2019
Pada dasarnya turunan dibedakan menjadi 3 yakni maju, mundur dan pusat. Pada nilai yang sama, turunan numerik pada jenis pusat merupakan turunan paling baik, dengan keberlanjutan maju dan mundur sebagai keakuratan yang sama. Akan tetapi, hal tersebut juga dipngaruhi oleh nilai h sebagai pengaruh terhadap truncation error. Berikut merupakan formula dan gambar grafik dari masing-masing jenis:
1. Turunan Hampiran Maju
2. Turunan Hampiran Mundur
2. Turunan Hampiran Pusat
Dengan menggunakan formula inilah, kita dapat menemukan hampiran nilai H. Sehingga turunan numerik dapat dilakukan
Kembali ke Halaman Awal Rilvan:
M. Rilvan Adinugraha