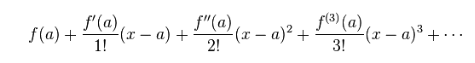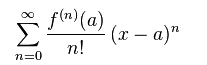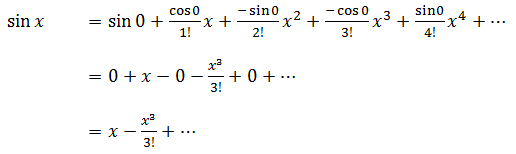PENDAHULUAN & TAYLOR METHOD

METODE NUMERIK

Berikut saya sertakan pencarian mengenai makna dari metode numerik menurut para ahli matematika:

1. Menurut Chapra dan Chanale, 1991, metode numerik adalah teknik di mana masalah matematika diformulasikan sedemikian rupa sehingga dapat diselesaikan oleh pengoperasian aritmetika

2. Susila. 1994 ; Ibraheem dan Hisyam, 2003, juga mengatakan bahwa metode numerik adalah teknik -teknik yang digunakan untuk merumuskan masalah matematika agar dapat diselesaikan han ya dengan operasi hitungan, yang terdiri dari operasi tambah, kurang, kali dan bagi

Dengan berpatokkan pada kedua hal tersebut, saya dapat menyimpulkan bahwa metode numerik merupakan suatu teknik yang dibentuk menggunakan sistem formulasi amtematik operasi arimatika guna menyelesaikan masalah-masalah tertentu yang telah disediakan.

TAYLOR'S METHOD

Deret taylor atau yang sering disebut sebagai Taylor's Methode merupakan sebuah perkawilan fungsi riil atau fungsi kompleksf(x) yang dihitung dengan mendeferensialkan hingga takhingga dalam sebuah persekitaran sebuah bilangan riil atau kompleksa adalah deret pangkat. Berikut rumus ataupun formula yang digunakan dalam menghitung hingga menggunakan deret taylor:

atau dapat disingkat menjadi persamaan berikut:

Kembali ke laman utama : M. Rilvan Adinugraha

DALAM KELAS

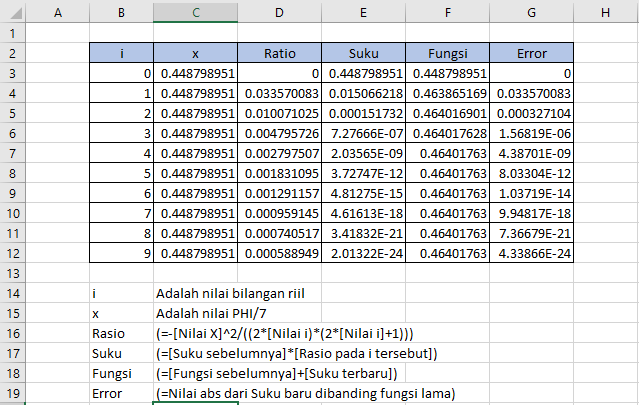
Peserta didik diminta untuk menggunakan excel untuk menyelesaikan persamaan SIN (PHI/7) dalam bentuk deret taylor. Langkah pertama yang perlu dilakukan adalah menyederhanakan persamaan tersebut dengan ringkas hingga mudah dikalkulasikan menggunakan persamaan yang ada di excel. Berikut penyelesaian yang didapatkan:

Berdasarkan nilai tersebut, ditemukan rasio antar satu nilai ke nilai lain dalam bentuk deret adalah -x^2/((2*i)*(2*i+1)). Maka penyelesaian dalam tabel dapat diselesaikan sebagai berikut. Beserta nilai-nilai rumus yang akan digunakan:

Kembali ke Halaman Awal Rilvan: [[1]]